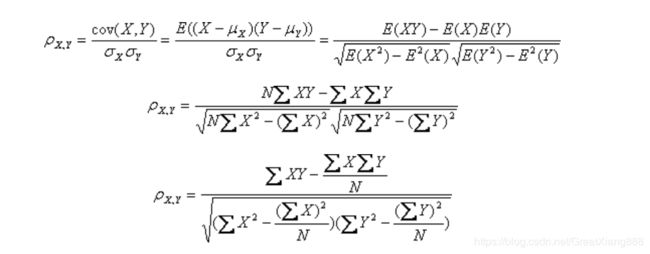皮尔逊(Pearson)相关系数 - 公式和代码实现

代码来源于：https://github.com/yaleimeng/Final_word_Similarity
我将其单独抽取、组合出来做讲解。

1. 简介

相关系数：考察两个变量之间的相关程度。相关系数越大，相关性越强。
皮尔逊相关也称为积差相关，是英国统计学家皮尔逊于20世纪提出的一种计算直线相关的方法。

2. 公式

三个公式都能计算正确结果，我们采用第三个公式来编程实现。

3. 代码实现

from math import sqrt

def multiply(a,b):
    #a,b两个列表的数据一一对应相乘之后求和
    sum_ab=0.0
    for i in range(len(a)):
        temp=a[i]*b[i]
        sum_ab+=temp
    return sum_ab

def cal_pearson(x,y):
    n=len(x)
    #求x_list、y_list元素之和
    sum_x=sum(x)
    sum_y=sum(y)
    #求x_list、y_list元素乘积之和
    sum_xy=multiply(x,y)
    #求x_list、y_list的平方和
    sum_x2 = sum([pow(i,2) for i in x])
    sum_y2 = sum([pow(j,2) for j in y])
    molecular=sum_xy-(float(sum_x)*float(sum_y)/n)
    #计算Pearson相关系数，molecular为分子，denominator为分母
    denominator=sqrt((sum_x2-float(sum_x**2)/n)*(sum_y2-float(sum_y**2)/n))
    return molecular/denominator

if __name__ == '__main__':
    x = [1.0, 0.8413847866522796, 1.0, 1.0, 0.7220196471443738, 0.8659769034282755, 0.8525472520008003, 1.0,
         0.8333703748448211, 0.389905372997432, 0.7323982353899079, 0.7636377912400188, 0.7182768399980969,
         0.2674857649974473, 0.4044950329998137, 0.34512807490538866, 0.18946683500771058, 0.30049731372316213,
         0.24729781155291156, 0.3094230131574097, 0.41238596985736753, 0.0, 0.0, 0.2684506957865521,
         0.14158316440453367, 0.35473275983651914, 0.0, 0.0, 0.0, 0.0]
    y = [0.98, 0.96, 0.96, 0.94, 0.925, 0.9025, 0.875, 0.855, 0.7775, 0.77, 0.7625, 0.7425, 0.7375, 0.705, 0.42, 0.415,
         0.29, 0.275, 0.2375, 0.2225, 0.2175, 0.21, 0.1575, 0.1375, 0.105, 0.105, 0.0325, 0.0275, 0.02, 0.02]
    res = cal_pearson(x,y)
    print(res) # 0.9171284464588204

4. 其他参考资料

如何理解皮尔逊相关系数（Pearson Correlation Coefficient）？ - 微调的回答 - 知乎