Topic: Binary Tree, BST, recursion/iteration.
// array to tree.
- leetcode 109. Convert Sorted List to Binary Search Tree -- To do
-
- Convert Sorted Array to Binary Search Tree
-
- LeetCode 106. Construct Binary Tree from Inorder and Postorder Traversal -- (好题!)
- leetcode 297.binary-tree-serialization -- done 1
- leetcode 449. Serialize and Deserialize BST -- done 1
- Leetcode 331. Verify Preorder Serialization of a Binary Tree (好题)-- done 1
BFS
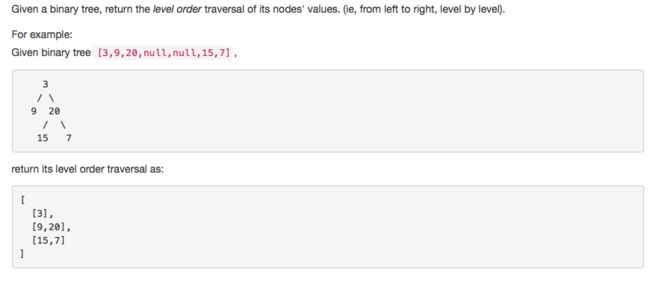
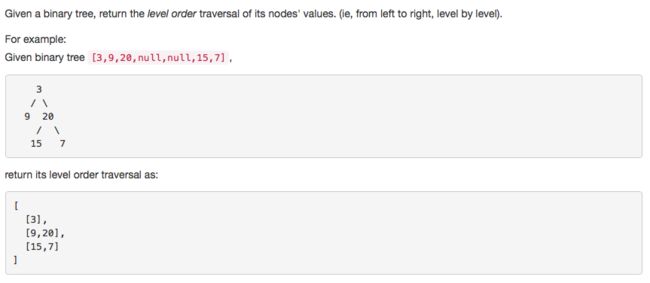
leetcode 102 Binary Tree Level Order Traversal
leetcode 107. Binary Tree Level Order Traversal II (除了与102一样的解法外还可以用dfs); -- TO DO
leetcode 116. Populating Next Right Pointers in Each Node
leetcode 116 Populating Next Right Pointers in Each Node -- To Do 分治法做最简单。
leetcode 285. Inorder Successor in BST
leetcode 102 Binary Tree Level Order Traversal
要点: (1) queue保证一层traverse完了再traverse下一层。 (2) 额外参数N用来分割layer
class Solution {
private int N = 0; // number of nodes in current layer
public List> levelOrder(TreeNode root) {
List> res = new ArrayList>();
if (root == null) return res;
Queue queue = new LinkedList();
queue.offer(root);
N = 1;
List layer = new ArrayList();
while (!queue.isEmpty()) {
TreeNode cur = queue.poll();
layer.add(cur.val);
N--;
if (cur.left != null) queue.offer(cur.left);
if (cur.right != null) queue.offer(cur.right);
if (N == 0) {
res.add(new ArrayList(layer));
layer.clear();
N = queue.size();
}
}
return res;
}
}
leetcode 116. Populating Next Right Pointers in Each Node
public class Solution {
public void connect(TreeLinkNode root) {
if(root == null || root.left == null) return;
connectNodes(root.left, root.right);
}
public void connectNodes(TreeLinkNode node1, TreeLinkNode node2) {
node1.next = node2;
if(node1.left != null) {
connectNodes(node1.right, node2.left);
connectNodes(node1.left, node1.right);
connectNodes(node2.left, node2.right);
}
}
}
leetcode 102 Binary Tree Level Order Traversal
public class BinaryTreeLevelOrderTraversal {
private int N = 0; // number of nodes in current layer
public List> levelOrder(TreeNode root) {
List> res = new ArrayList>();
if (root == null) return res;
Queue queue = new LinkedList();
queue.offer(root);
N = 1;
List layer = new ArrayList();
while (!queue.isEmpty()) {
TreeNode cur = queue.poll();
layer.add(cur.val);
N--;
if (cur.left != null) queue.offer(cur.left);
if (cur.right != null) queue.offer(cur.right);
if (N == 0) {
res.add(new ArrayList(layer));
layer.clear();
N = queue.size();
}
}
return res;
}
}
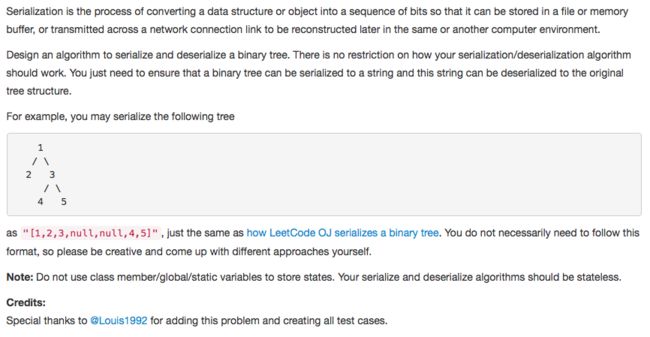
leetcode 297. Serialize and Deserialize Binary Tree
非递归的解法:http://codenuggets.com/2016/07/16/binary-tree-serialization
非递归遍历(使用queue -- 注意此处是bfs遍历!preorder是用stack)
反序列化:仍然维护一个队列,进队时创建节点,出队时从String array里面拿两个(if possible)出来。<-> 分析:考虑bfs遍历时,每次出队列都会把2个节点(左右children)加入队列,
递归解法很好用
- 使用了preorder traversal的序列
- 反序列化较难。这里用了一个queue,使得递归可以顺利实现。
- 2.1 除了queue,可以直接操作String array(需要一个额外的field来给array计数)
- 2.2另外可以用StringTokenizer
public class SerializeAndDeserializeBinaryTree {
// Encodes a tree to a single string.
public String serialize(TreeNode root) {
StringBuilder res = new StringBuilder();
serializeHelper(root, res);
return res.toString();
}
/*
* Result is: 1,4,#,#,2,3,#,#,# <-> 1 + ,4 + ,# + ,# + ,2 + ,3 + ,# + ,# + ,#
* Notice that if comma is put after integer then there is no way to eliminate the last comma.
*/
private void serializeHelper(TreeNode root, StringBuilder res) {
if (res.length() > 0) res.append(","); // the root has not comma ahead.
if (root == null) {
res.append("#");
return;
}
res.append(root.val);
serializeHelper(root.left, res);
serializeHelper(root.right, res);
}
// Decodes your encoded data to tree.
public TreeNode deserialize(String data) {
String[] vals = data.split(",");
System.out.println(vals.length);
LinkedList queue = new LinkedList();
for (String s : vals)
queue.offer(s);
return deserializeHelper(queue);
}
private TreeNode deserializeHelper( LinkedList queue) {
if (queue.isEmpty()) return null;
String val = queue.poll();
if (val.equals("#")) return null;
// else val is an integer
TreeNode root = new TreeNode(Integer.parseInt(val));
root.left = deserializeHelper(queue);
root.right = deserializeHelper(queue);
return root;
}
}
leetcode 449. Serialize and Deserialize BST
与 297(Serialize and Deserialize BT)的区别在于:
BST的特性可以让序列化更compact, i.e. 不需要“#”来表示null.
public class SerializeAndDeserializeBST {
// Encodes a tree to a single string.
public String serialize(TreeNode root) {
// 用前序遍历来做序列化。string中不包含null
StringBuilder res = new StringBuilder();
serializeHelper(root, res);
return res.toString();
}
private void serializeHelper(TreeNode root, StringBuilder res) {
if (root == null) return;
if (res.length() != 0) res.append(",");
res.append(root.val);
serializeHelper(root.left, res);
serializeHelper(root.right, res);
}
// Decodes your encoded data to tree.
public TreeNode deserialize(String data) {
// 注意这个corner case
if (data.equals("")) return null;
String[] vals_string = data.split(",");
int[] vals = new int[vals_string.length];
for (int i = 0; i< vals_string.length; i++) {
vals[i] = Integer.parseInt(vals_string[i]);
}
return deserializeHelper(vals, 0, vals.length-1);
}
private TreeNode deserializeHelper(int[] vals, int start, int end) {
if (start > end) return null;
int rootVal = vals[start];
TreeNode root = new TreeNode(rootVal);
// find the FIRST value that larger than rootVal -- index is rightStart
// applies to start == end as well
int rightStart, i = start + 1;
while (i <= end) {
if (vals[i] > rootVal) break;
I++;
}
rightStart = I; // 如果没有找到的话, rightStart = i = end+1
root.right = deserializeHelper(vals, rightStart, end);
root.left = deserializeHelper(vals, start+1, rightStart-1);
return root;
}
解析: 递归反序列化
如下bst的preorder traversal是2,1,4,3
----2
--1 --- 4
-----3
2必然是root节点,下一步要找到第一个比2大的数(也就是4).一旦找到:
1)则[1]构成了root的左子树 (需要反序列化)
2)[4,3]构成了root的右子树(也需要反序列化)
从而将原问题转化成递归求解子问题。
除了这种递归解法,geekforgeek还有一种非递归的解法,很巧妙地用到了stack。可以参考。
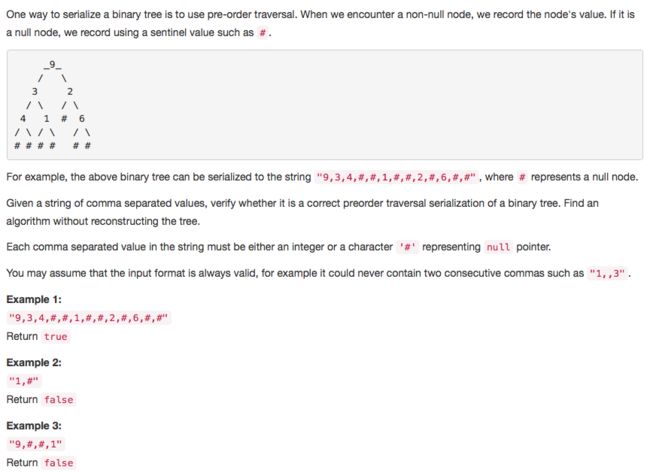
Leetcode 331. Verify Preorder Serialization of a Binary Tree (好题)
这题和Leetcode 297(Serialize and Deserialize BT)非常相似。
要求是不重构树
public class VerifyPreorderSerializationOfBinaryTree {
public boolean isValidSerialization(String preorder) {
if (preorder.equals("")) return false; // corner case
String[] tokens = preorder.split(",");
LinkedList queue = new LinkedList();
queue.addAll(Arrays.asList(tokens));
return checkSerialization(queue) && queue.isEmpty();
}
private boolean checkSerialization(LinkedList queue) {
if (queue.isEmpty()) return false;
String val = queue.poll();
if (val.equals("#"))
return true;
// else integer
return checkSerialization(queue) && checkSerialization(queue); // check left and right;
}
}
解析:注意到这题实际给出的序列化就是preorder serialization,所以思路和297的deserialization是完全一样的。
要点:用queue每次pop出一个string;
重构失败只会因为两种情况:
- 该有next string的时候没有了,i.e. "1,#" -- 此时会在
checkSerialization中出现queue为空。- 不该有next string的时候仍有next string, i.e., 在
isValidSerialization中要检查调用checkSerialization完毕后queue已经全部排空。
285. Inorder Successor in BST
// 参考range的解法
public TreeNode successor(TreeNode root, int target) {
if (root == null) return null;
if (target < root.val) { //a. 左子树中没有更小的话那就是root啦!
TreeNode temp = successor(root.left, target);
return temp == null ? root : temp;
}
else if (target > root.val) { //b. 显然要在右子树中找。
return successor(root.right, target);
} else { //c. target == root.val 走到这一步说明上面(a步暂时)还没找到
// 右子树中有的话就是结果,没有的话对上层(a)判断也有用。
return successor(root.right, target);
}
}
解析: 这题是道非常经典的BST递归解法题。
要点: 整个BST的操作#全部# 都可以用递归简洁地完成!
下面列了一些(Robert Sedgewick)常见的BST操作(floor和ceiling跟这个successor很相似)
// recursive solution
public class SearchInBST {
// 左子树找不到就在右子树找。
public TreeNode search(TreeNode root, int target) {
if (root == null) return null;
if (root.val == target) return root;
else if (root.val < target)
return search(root.right, target);
else
return search(root.left, target);
}
public Iterable range(TreeNode root, int lo, int hi) {
LinkedList queue = new LinkedList();
rangeHelper(root, queue, lo, hi);
return queue;
}
private void rangeHelper(TreeNode node, LinkedList queue, int lo, int hi) {
if (node == null) return;
if (lo < node.val) rangeHelper(node.left, queue, lo, hi);
if (lo <= node.val && node.val <= hi) queue.offer(node);
if (node.val < hi) rangeHelper(node.right, queue, lo, hi);
}
// 参考range的解法
public TreeNode successor(TreeNode root, int target) {
if (root == null) return null;
if (target < root.val) { //a. 左子树中没有更小的话那就是root啦!
TreeNode temp = successor(root.left, target);
return temp == null ? root : temp;
}
else if (target > root.val) { //b. 显然要在右子树中找。
return successor(root.right, target);
} else { //c. target == root.val 走到这一步说明上面(a步暂时)还没找到
// 右子树中有的话就是结果,没有的话对上层(a)判断也有用。
return successor(root.right, target);
}
}
public TreeNode min(TreeNode root) {
if (root.left == null) return root;
else return min(root.left);
}
public TreeNode max(TreeNode root) {
if (root.right == null) return root;
else return max(root.right);
}
}
注: 这里包含了
search,range,successor,min,max。
注意min/max方法中: 左/右子树不存在再化为子问题。
109 Convert Sorted List to Binary Search Tree (medium)
108 Convert Sorted Array to Binary Search Tree (easy)
两题很相似。array好做因为access array element简单。只用
mid = lo + (hi-lo)/2就可以得到中间数
LinkList可以用双指针* 来求区间中点!
public class ConvertSortedListToBST {
public TreeNode sortedListToBST(ListNode head) {
if (head == null) return null;
return toBST(head, null);
}
private TreeNode toBST(ListNode head, ListNode tail) {
if (head == tail) return null;
ListNode slow = head;
ListNode fast = head;
// 这个双指针(在list中)找中点 太经典了!!!
//注意是 fast != tail 不是 != null.
while (fast != tail && fast.next != tail) {
slow = slow.next;
fast = fast.next.next;
}
TreeNode root = new TreeNode(slow.val);
root.left = toBST(head, slow);
root.right = toBST(slow.next, tail);
return root;
}
}
解释: complexity O(nlogn) -- n 层迭代,每层需要指针遍历O(n)
public TreeNode sortedArrayToBST(int[] A) {
if (A == null) return null;
return buildBST(A, 0, A.length-1);
}
private TreeNode buildBST(int[] A, int start, int end) {
if (start > end) return null;
int mid = start + (end - start) / 2;
TreeNode root = new TreeNode(A[mid]);
root.left = buildBST(A, start, mid-1);
root.right = buildBST(A, mid+1, end);
return root;
}
note:上面是108的解答。
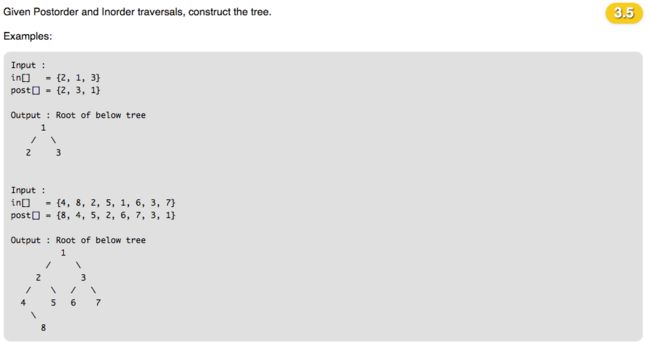
LeetCode 106. Construct Binary Tree from Inorder and Postorder Traversal
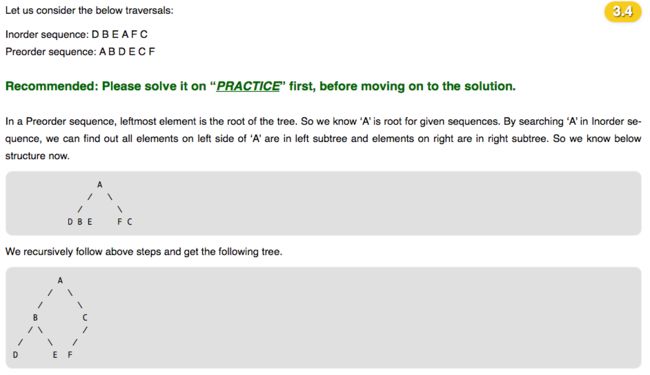
这道题有道原型体:Construct Tree from given Inorder and Preorder traversals https://www.geeksforgeeks.org/construct-tree-from-given-inorder-and-preorder-traversal/
这题真是recursion的经典题。
要点:需要意识到preorder怎么使用。
inorder的构造是left -> current -> right
buildTree时必然要先找到current val然后构造current(所有node全部都是这么构造的)。之后再递归构造left 和 right
=====> 这样的构造node的顺序是 current->left->right正好是preorder traversal.所以preorder array是完全按照顺利来遍历的。只需要维护一个field,让递归时也能access到正确的node就可以了。
public class BinaryTreeConstructionInorderPreorderTraversal {
private int preIndex;
public TreeNode buildTree(int[] inorder, int[] preorder) {
preIndex = 0;
return buildTree(inorder, preorder, 0, inorder.length-1);
}
private TreeNode buildTree(int[] inorder, int[] preorder, int inStart, int inEnd) {
if (inStart > inEnd) return null;
TreeNode root = new TreeNode(preorder[preIndex++]);
int curInIndex = inIndex(inorder, preorder[preIndex-1], inStart, inEnd);
// 一定要先递归构造左子树, 才能让preIndex正常++
root.left = buildTree(inorder, preorder, inStart, curInIndex-1);
root.right = buildTree(inorder, preorder, curInIndex+1, inEnd);
return root;
}
// 假设target是存在的
public int inIndex(int[] inorder, int target, int inStart, int inEnd) {
int i = 0;
for (i = inStart; i <= inEnd; i++) {
if (inorder[i] == target)
break;
}
return i; //不考虑越界问题。
}
}
解析,考虑树: root = node(1); root.left = node(2); root.left.right = node(3); root.right = node(4);
inorder traversal: 2 3 左 | 1 |4 右
preorder traversal: 1 | 2 3 左 | 4右
postorder traversal 3 2 左 | 4 右|1
- 无论pre还是post都是必须的,因为可以直接通过首/尾元素构造root节点(此处为1)。
- 再inorder 找到首/尾元素就可以把inorder分成两个子序列[inStart, inIndex-1] [inIndex+1, inEnd] 分别对应root的左右子树。
- 仔细想,这题跟其他重建BT的题(i.e. leetcode 297) 也有点像,每次只重建#一个#node!然后递归重建该节点的左右children。正因为如此我们可以意识到对preorder/postorder元素的遍历是一个一个地进行的。
- preorder的遍历是root->左子树->右子树, 所以递归时先buildTree左子树,再右子树。
- postorder的遍历(array倒叙~)是root->右子树->左子树,所以递归时先buildTree右子树,再左子树
public class BinaryTreeConstructionInorderPostorderTraversal {
private int curPostIndex;
public TreeNode buildTree(int[] inorder, int[] postorder) {
curPostIndex = postorder.length-1;
return buildTree(inorder, postorder, 0, inorder.length-1);
}
/*
* 这题跟其他重建BT的题也有点像,每次只重建一个node!然后递归重建该节点的左右children
*/
private TreeNode buildTree(int[] in, int[] post, int inStart, int inEnd) {
if (inStart > inEnd) return null;
TreeNode root = new TreeNode(post[curPostIndex--]);
int curInIndex = inIndex(in, post[curPostIndex+1], inStart, inEnd);
//一定要先right tree!!!!
root.right = buildTree(in, post, curInIndex+1, inEnd);
root.left = buildTree(in, post, inStart, curInIndex-1);
return root;
}
// assume target always present in array
private int inIndex(int[] in, int target, int inStart, int inEnd) {
int i = 0;
for (i = inStart; i <= inEnd; i++) {
if (in[i] == target)
break;
}
return I;
}
}
解析上面已经分析过了,昨晚pre+inorder, post+inorder应该就迎刃而解。