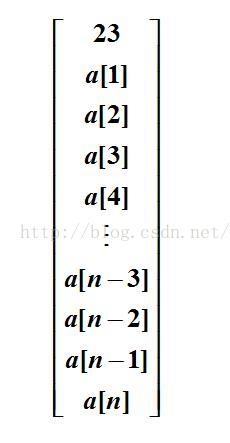HDU5015 - 233 Matrix - 思维+矩阵快速幂

1.题目描述：

233 Matrix

Time Limit: 10000/5000 MS (Java/Others)    Memory Limit: 65536/65536 K (Java/Others)
Total Submission(s): 2118    Accepted Submission(s): 1237

Problem Description

In our daily life we often use 233 to express our feelings. Actually, we may say 2333, 23333, or 233333 ... in the same meaning. And here is the question: Suppose we have a matrix called 233 matrix. In the first line, it would be 233, 2333, 23333... (it means a _0,1 = 233,a _0,2 = 2333,a _0,3 = 23333...) Besides, in 233 matrix, we got a _i,j = a _i-1,j +a _i,j-1( i,j ≠ 0). Now you have known a _1,0,a _2,0,...,a _n,0, could you tell me a _n,m in the 233 matrix?

 

Input

There are multiple test cases. Please process till EOF.

For each case, the first line contains two postive integers n,m(n ≤ 10,m ≤ 10 ⁹). The second line contains n integers, a _1,0,a _2,0,...,a _n,0(0 ≤ a _i,0 < 2 ³¹).

 

Output

For each case, output a _n,m mod 10000007.

 

Sample Input

1 1 1 2 2 0 0 3 7 23 47 16

 

Sample Output

234 2799 72937

Hint

 

Source

2014 ACM/ICPC Asia Regional Xi'an Online

 

Recommend

hujie   |   We have carefully selected several similar problems for you:   6018  6017  6016  6015  6014 

2.题意概述：

有一个矩阵横排第一行初始是0,233,2333,23333...，然后给出计算公式a[i][j] = a[i - 1][j] + a[i][j - 1]，然后给出了n和m和第一列的各值要求计算a[n][m]的值。

3.解题思路：

因为数据量很大，暴力求解肯定是不行的。必定超时，虽然给定的时间是5秒钟。

那接下来就是推公式了，而我最终也真的推出来个公式，但很遗憾，它只有当n和m相等的时候才成立，可是n最大才为10，这种思路也就被否定了。

既然给定的是一个矩阵的形式，难道可以用矩阵快速幂搞出来？可以试试。注意一点，如果能构造出来快速幂的话，也只有按列来推。

因为a[0][1]=233，a[0][2]=2333，a[0][3]=23333，…………，所以有a[0][i]=10*a[0][i-1]+3（i>1，a[0][1]=233）

如果令a[0][0]=23，那么a[0][i]=10*a[0][i-1]+3（i>0，a[0][0]=23）

则对于n+1行，m+1列的矩阵A，有

第一列（下标j=0）

第二列（下标j=1）

第三列（下标j=2）

对上述矩阵的各列适当变形得：

第一列（下标j=0）

第二列（下标j=1）

第三列（下标j=2）

所以有

根据上面的递推公式，我们可以构造矩阵得，

（其中）

4.AC代码：

#include 
#include 
#include 
using namespace std;
struct matrix
{
	__int64 mat[15][15];

	matrix()
	{
		memset(mat, 0, sizeof(mat));
	}
};
int n;
const int mod = 10000007;
matrix mul(matrix B, matrix A)         //左乘列矩阵
{
	int i, j, k;
	matrix C;
	for (i = 1; i <= n + 2; i++)
		for (j = 1; j <= n + 2; j++)
			for (k = 1; k <= n + 2; k++)
				C.mat[i][j] = (C.mat[i][j] + B.mat[i][k] * A.mat[k][j]) % mod;
	return C;
}
matrix powmul(matrix A, int m)
{
	matrix ans;
	for (int i = 1; i <= n + 2; i++)
		ans.mat[i][i] = 1;              //单位矩阵
	while (m > 0)
	{
		if (m & 1)
			ans = mul(ans, A);
		A = mul(A, A);
		m >>= 1;
	}
	return ans;
}
int main()
{
	//freopen("input.txt", "r", stdin);
	int m;
	while (scanf("%d%d", &n, &m) != EOF)
	{
		matrix A, B;
		A.mat[1][1] = 23;                //原矩阵首元素为23，使每一列都可以被转换（原来第二列不行
		for (int i = 1; i <= n; i++)
			scanf("%d", &A.mat[i + 1][1]);
		A.mat[n + 2][1] = 3;

		for (int i = 1; i <= n + 1; i++)
			B.mat[i][1] = 10;
		for (int i = 1; i <= n + 2; i++)
			B.mat[i][n + 2] = 1;
		for (int i = 1; i < n + 2; i++)
			for (int j = 2; j <= i; j++)
				B.mat[i][j] = 1;     //转移矩阵的下三角单位阵

		B = powmul(B, m);
		A = mul(B, A);               //A除了第一列之外所有的元素都是0，相当于列矩阵

		cout << A.mat[n + 1][1] << endl;
	}

	return 0;
}