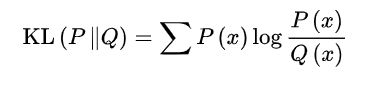深度学习-变分自编码器（VAE）生成MNIST手写数字图片

MNIST数据集：数据集下载

下载好数据集新建MNIST文件夹，再在里边建一个raw文件夹，数据集解压后放到raw文件夹中（数据集后缀为.gz，不需要再解压了）

简介：

变分自编码器（Variational Autoencoder,VAE）是生成式模型（Ggenerative Model）的一种，另一种常见的生成式模型是生成式对抗网络（Generative Adversial Network，GAN）

原理：

以MNIST为例，再看过几千张手写数字图片之后，能够进行模仿，并生成一些类似的图片，这些图片在原始数据中并不存在，有一些变化但是看起来很相似，也就是说，需要学会原始数据X的分布，这样根据数据的分布就能轻松地产生新样本。

                                                                                         P(x)------数据分布

 

但是数据分布地估计不是件容易地事，尤其是当数据量不足的时候，因此可以使用一个隐变量z，由z经过一个复杂的映射得到x，并且假设z服从高斯分布（正态分布）。

                                                                                              x=f(z;θ)

因此只需要学习隐变量所服从高斯分布的参数（高斯分布的均值和方差），以及映射函数，即可得到原始数据的分布。为了学习隐变量所服从高斯分布的参数，需要得到z足够多的样本，然而z的样本并不能直接获得，因此还需要一个映射函数（条件概率分布），从已有的x样本中得到对应的z样本。

                                                                                             z=Q（x）

 

除了重构误差（出来的x和进去的x重构一下，让它尽可能相似），由于在VAE中假设隐变量z服从高斯分布，因此encoder对应的条件概率分布，应当和高斯分布尽可能相似。可以用相对熵，又称KL散度（Kullback-Leibler Divergence），来衡量两个分布的差异，或者说距离，但是相对熵时非对称。

因此，变分自编码器和自编码器很相似，从数据本身，经编码得到隐层表示，经解码还原，但是VAE和AE还是有区别的，区别如下：

1.AE中隐层表示的分布未知，而VAE中隐变量服从高斯分布。

2.AE中学习的是encoder和decoder，VAE中还学习了隐变量的分布，包括高斯分布的均值和方差。

3.AE只能从一个x，得到对应的重构x。

4.VAE可以产生新的z，从而得到新的x，即产生新的样本。

 

代码：

import os
import torch
import torch.nn as nn
import torch.nn.functional as F
import torchvision
from torchvision import transforms
from torchvision.utils import save_image

# 配置GPU或CPU设置
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')

# 创建目录保存生成的图片
sample_dir = 'samples'
if not os.path.exists(sample_dir):
    os.makedirs(sample_dir)

# 超参数设置
image_size = 784   #图片大小
h_dim = 400
z_dim = 20
num_epochs = 15   #15个循环
batch_size = 128   #一批的数量
learning_rate = 1e-3   #学习率

# 获取数据集
dataset = torchvision.datasets.MNIST(root='./data',
                                     train=True,
                                     transform=transforms.ToTensor(),
                                     download=True)

# 数据加载，按照batch_size大小加载，并随机打乱
data_loader = torch.utils.data.DataLoader(dataset=dataset,
                                          batch_size=batch_size,
                                          shuffle=True)


# VAE模型
class VAE(nn.Module):
    def __init__(self, image_size=784, h_dim=400, z_dim=20):
        super(VAE, self).__init__()
        self.fc1 = nn.Linear(image_size, h_dim)
        self.fc2 = nn.Linear(h_dim, z_dim)
        self.fc3 = nn.Linear(h_dim, z_dim)
        self.fc4 = nn.Linear(z_dim, h_dim)
        self.fc5 = nn.Linear(h_dim, image_size)

    # 编码，学习高斯分布均值与方差
    def encode(self, x):
        h = F.relu(self.fc1(x))
        return self.fc2(h), self.fc3(h)

    # 将高斯分布均值与方差参数重表示，生成隐变量z  若x~N(mu, var*var)分布,则(x-mu)/var=z~N(0, 1)分布
    def reparameterize(self, mu, log_var):
        std = torch.exp(log_var / 2)
        eps = torch.randn_like(std)
        return mu + eps * std

    # 解码隐变量z
    def decode(self, z):
        h = F.relu(self.fc4(z))
        return F.sigmoid(self.fc5(h))

    # 计算重构值和隐变量z的分布参数
    def forward(self, x):
        mu, log_var = self.encode(x)  # 从原始样本x中学习隐变量z的分布，即学习服从高斯分布均值与方差
        z = self.reparameterize(mu, log_var)  # 将高斯分布均值与方差参数重表示，生成隐变量z
        x_reconst = self.decode(z)  # 解码隐变量z，生成重构x’
        return x_reconst, mu, log_var  # 返回重构值和隐变量的分布参数


# 构造VAE实例对象
model = VAE().to(device)
print(model)
"""VAE(
  (fc1): Linear(in_features=784, out_features=400, bias=True)
  (fc2): Linear(in_features=400, out_features=20, bias=True)
  (fc3): Linear(in_features=400, out_features=20, bias=True)
  (fc4): Linear(in_features=20, out_features=400, bias=True)
  (fc5): Linear(in_features=400, out_features=784, bias=True)
)"""

# 选择优化器，并传入VAE模型参数和学习率
optimizer = torch.optim.Adam(model.parameters(), lr=learning_rate)
# 开始训练一共15个循环
for epoch in range(num_epochs):
    for i, (x, _) in enumerate(data_loader):
        # 前向传播
        x = x.to(device).view(-1,image_size)  # 将batch_size*1*28*28 ---->batch_size*image_size  其中，image_size=1*28*28=784
        x_reconst, mu, log_var = model(x)  # 将batch_size*748的x输入模型进行前向传播计算,重构值和服从高斯分布的隐变量z的分布参数（均值和方差）

        # 计算重构损失和KL散度
        # 重构损失
        reconst_loss = F.binary_cross_entropy(x_reconst, x, size_average=False)
        # KL散度
        kl_div = - 0.5 * torch.sum(1 + log_var - mu.pow(2) - log_var.exp())

        # 反向传播与优化
        # 计算误差(重构误差和KL散度值)
        loss = reconst_loss + kl_div
        # 清空上一步的残余更新参数值
        optimizer.zero_grad()
        # 误差反向传播, 计算参数更新值
        loss.backward()
        # 将参数更新值施加到VAE model的parameters上
        optimizer.step()
        # 每迭代一定步骤，打印结果值
        if (i + 1) % 10 == 0:
            print("Epoch[{}/{}], Step [{}/{}], Reconst Loss: {:.4f}, KL Div: {:.4f}"
                  .format(epoch + 1, num_epochs, i + 1, len(data_loader), reconst_loss.item(), kl_div.item()))

    with torch.no_grad():
        # 保存采样值
        # 生成随机数 z
        z = torch.randn(batch_size, z_dim).to(device)  # z的大小为batch_size * z_dim = 128*20
        # 对随机数 z 进行解码decode输出
        out = model.decode(z).view(-1, 1, 28, 28)
        # 保存结果值
        save_image(out, os.path.join(sample_dir, 'sampled-{}.png'.format(epoch + 1)))

        # 保存重构值
        # 将batch_size*748的x输入模型进行前向传播计算，获取重构值out
        out, _, _ = model(x)
        # 将输入与输出拼接在一起输出保存  batch_size*1*28*（28+28）=batch_size*1*28*56
        x_concat = torch.cat([x.view(-1, 1, 28, 28), out.view(-1, 1, 28, 28)], dim=3)
        save_image(x_concat, os.path.join(sample_dir, 'reconst-{}.png'.format(epoch + 1)))

第一张第15张