shell函数语言实现斐波那契数列/汉诺塔等问题

一、斐波那契数列又称黄金分割数列，因数学家列昂纳多·斐波那契以兔子繁殖为例子而引入，故又称为“兔子数列”，指的是这样一个数列：0、1、1、2、3、5、8、13、21、34、……，斐波纳契数列以如下被以递归的方法定义：F（0）=0，F（1）=1，F（n）=F(n-1)+F(n-2)（n≥2）利用函数，求n阶斐波那契数列。

1.递归实现，但是普通计算机只能算30以内的斐波那契数列，稍大一点基本就算不过来了。

func_Fibonacci(){
   tmp=$1
    if [ $tmp -le 2 ];then
        echo 1
    else        
        F1=`Fibonacci $[tmp-1]`
        F2=`Fibonacci $[tmp-2]`
        echo $[F1+F2]
    fi
}

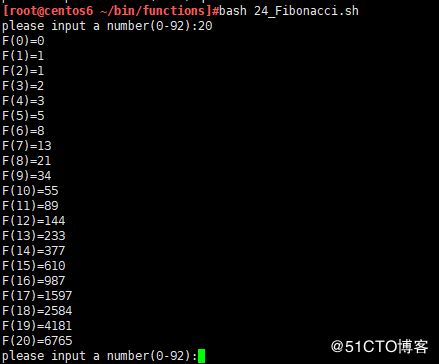
2.迭代循环算法，只能算到92以内的斐波那契数列，这里推荐用c语言编程。后附C语言编程

func_Fibonacci(){
    tmp=$1
    first=1
    declare -i i=0
    second=1
    last=1
    if [ $tmp -eq 1 -o $tmp -eq 2 ] ;then
        echo "F($tmp)=1"
    elif [ $tmp -eq 0 ];then
        echo  "F($tmp)=0"
    else
        for i in `seq 3 $tmp`;do
            let last=$first+$second
            let first=$second
            let second=$last
        done
        echo  "F($tmp)=$last"
    fi
}   

trap 'echo Ctrl+C\\ is not work ,Please type q or quit to exit' 1 2 3 15
while : ;do
    read -p "please input a number(0-92):" num
    if [[ $num =~ ^[Qq]([Uu][Ii][Tt])?$ ]] ;then
        break 
    elif [[ $num =~ ^[0-9]+$ ]] && [ $num -le 92 ] ;then
        func_Fibonacci $num
    else
        echo "Error:please enter a positive number less than 92!"
    fi
    unset num
done 

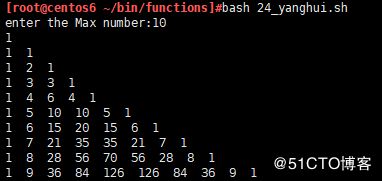
二、打印杨辉三角

#!/bin/bash
yanghui(){
    tmp=$1
    i=0
    while [ $i -ne `expr $tmp + 1` ]  
    do
        if [ $i -eq $tmp ]||[ $i -eq 0 ]
        then
            echo -n 1  
        else
            echo -n $(expr $2 + $3)  
            shift
        fi
        echo -n " "  
        i=`expr $i + 1`
    done

}
if [ $# -ne 1 ]
then
   read -p  "enter the Max number:"  COUNT
else
    COUNT=$1
fi
i=0
while [ $i -ne  $COUNT ]  
do
    tmp=(`yanghui $i ${tmp[*]}`)
    echo ${tmp[*]}  
    i=`expr $i + 1`
done 

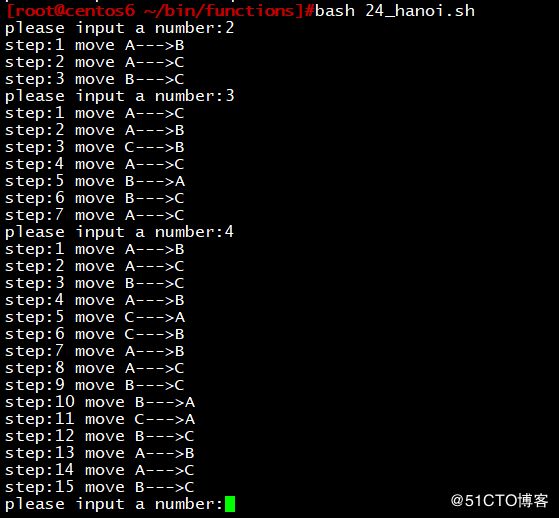
三、汉诺塔（又称河内塔）问题是源于印度一个古老传说。大梵天创造世界的时候做了三根金刚石柱子，在一根柱子上从下往上按照大小顺序摞着64片黄金圆盘。大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。并且规定，在小圆盘上不能放大圆盘，在三根柱子之间一次只能移动一个圆盘，利用函数，实现N片盘的汉诺塔的移动步骤。

#!/bin/bash
function Hanoi(){
    local tmp=$1
    if [ $tmp -eq 1 ] ;then
        let i++
        echo "step:$i move $2--->$4"      #move A to C
    else
        Hanoi $[$1-1] $2 $4 $3 # move the n-1 plate to B
        let i++
        echo "step:$i move $2--->$4" #move the bigest  plate to C
        Hanoi $[$1-1] $3 $2 $4  #move the n-1 plate to C
    fi
}

trap 'echo Ctrl+C is not work ,Please type q or quit to exit' 2
while : ;do
    read -p "please input a number:" tmp
    declare -i i=0
    if [[ $tmp =~ ^[Qq]([Uu][Ii][Tt])?$ ]] ;then
        break 
    elif [[ $tmp =~ ^[0-9]+$ ]] ;then
        Hanoi $tmp A B C
    else
        echo "Error:please input a positive number!"
    fi
    unset tmp
done

PS:C编程的fib函数，要求是不超过1000位Fibonacci数（大神编写的），有兴趣的可以下载编译试一下。

#include 
#include 

/*自定义的大数表示方法
结构体数组中的每一个int表示一个不超过 10 0000 0000 的数,
它是小于有符号int的最大值的,也就是说把一个很大的数拆分成
多个部分表示,就像我们在做两个数相加时,一位一位相加一样,
我只是用程序9位9位的加,取代人工的1位加法
*/

//要求是不超过1000位Fibonacci数,我这里就取MAX_BIG位,最多能表示
//的Fibonacci位数就是 MAX_BIG*9 = 120*9 = 1080位
//我这里用BIG_INTEGER[0]表示最低位
#define MAX_BIG     120
typedef struct{
    //+1:可能产生最高位进位,但我不管,直接丢弃(不然VS2012会报栈被破坏,
    //栈确实会被破坏,VS2012挻智能的)
    unsigned int big[MAX_BIG+1];
}BIG_INTEGER;

#define BIG_BASE        1000000000         //进制,不知道不要乱改
/*******************************************************
函数:calc@12
功能:a+b -> c, 大数加法
参数:a,b - 加数; c:和
返回:(无)
*******************************************************/
void calc(BIG_INTEGER* a, BIG_INTEGER* b,BIG_INTEGER* c)
{
    unsigned int sum=0;
    int i=0;

    /**************************
    以下循环计算一次加法:
        加数1:abcd
        加数2:efgh
        结果:(a+e+x)(b+f+x)(c+g+x)(d+h+x)
    其中:
        abcd,efgh在这里各代表一个9位数
        x代表来自低位的进位
    ***************************/
    memset(c,0,sizeof(BIG_INTEGER));
    for(i=0; ibig[i] = a->big[i] + b->big[i] + c->big[i];  //做1次9位加,记得加上本身
        c->big[i+1] = c->big[i]/BIG_BASE;               //高位加上结果的进位
        c->big[i] = c->big[i] % BIG_BASE;               //当前位只保留余数
    }
}

/************************************************************
函数:fibonacci@4
功能:计算第n位的菲波那契数值
参数:n:第n位, 最低为1
************************************************************/
void fibonacci(int n)
{
    BIG_INTEGER a = {0};
    BIG_INTEGER b = {0};
    BIG_INTEGER c = {0};
    int i=0;

    if(n<=1){
        printf("%d\n",n==1);
        return;
    }

    //Fibonacci:1,1,2,3,5,8,...
    //为保证第一次计算(n=2)时的结果,所以初值为:a=0,b=1 => c=1
    a.big[0] = 0;
    b.big[0] = 1;

    /**************************
    以下循环计算类似小数的Fibonacci:
        f3 = f1 + f2;
        f1 = f2;
        f2 = f3;
    ***************************/
    for(i=2; i<=n; i++){
        calc(&a,&b,&c);
        memcpy(&a,&b,sizeof(BIG_INTEGER));
        memcpy(&b,&c,sizeof(BIG_INTEGER));
    }
    //该for循环忽略输出从最高位开始的为0的一个数值位(9位)
    //当然, 条件 i>0 是必须的,你知道为什么吗?
    for(i=MAX_BIG-1; c.big[i]==0 && i>0; i--)
        ;
    //对于最高位:不需要输出前导的'0'
    printf("%u", c.big[i--]);
    //然后按9位分解输出每个数值位,这个一定要记得输出前导0,
    //一开始我没注意到,就出了问题
    while(i>=0){
        printf("%09u",c.big[i]);
        i--;
    }
    printf("\n");
}

int main(void)
{
    int n;
    scanf("%d",&n);
    fibonacci(n);
    return 0;
}  

真的很快1s不到。