03_集成学习(Ensemble Learning)里的堆叠(Stacking)
集成学习(Ensemble Learning)里的堆叠
- 堆叠
- 回归问题
- 分类问题
- 写stacking的模块
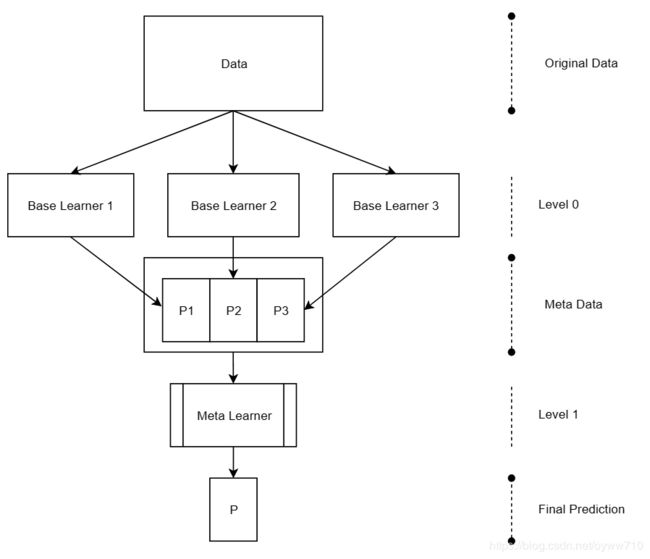
堆叠是我们将要学习的第二种集成学习技术。与投票一起,它属于非生成方法类,因为它们都使用经过单独训练的分类器作为基础学习器。元学习是广义的机器学习术语。它具有多种含义,但通常需要将元数据用于特定问题才能解决。它的应用范围从更有效地解决问题到设计全新的学习算法,这是一个正在发展的研究领域。堆叠是元学习的一种形式。主要思想是,我们使用基础学习器来生成问题数据集的元数据,然后使用另一个称为元学习器的学习器来处理元数据。基础学习器被认为是0级学习器,而元学习器被认为是1级学习器。换句话说,元学习器堆叠在基础学习器之上,因此名称堆叠。在堆叠过程中,我们没有明确定义组合规则,而是训练了一个模型,该模型学习如何最佳地组合基础学习器的预测。元学习器的输入数据集由基础学习器的预测(元数据)组成,如图所示:
如前所述,我们需要元数据来训练和操作我们的集。在操作阶段,我们仅传递来自基础学习器的数据。另一方面,训练阶段要复杂一些。我们希望元学习器发现基础学习器之间的优缺点。尽管有些人认为我们可以在训练集上训练基础学习器,对其进行预测,然后使用这些预测来训练我们的元学习器,但这会引起差异。我们的元学习器将发现(基础学习器)已经看到的数据的优缺点。由于我们要生成具有不错的预测(训练样本外)性能的模型,而不是描述性(训练样本内)性能,因此必须采用另一种方法。另一种方法是将我们的训练集分为基础学习器训练集和元学习器训练(验证)集。这样,我们仍将保留一个真实的测试集,在这里我们可以测量集成的性能。这种方法的缺点是我们必须将一些实例给验证集。此外,验证集合大小和训练集集合大小都将小于原始训练集合大小。因此,首选方法是利用K折交叉验证。对于每个K,基础学习器将在K-1折中进行训练,并在第K折中进行预测,从而生成最终训练元数据的100 / K百分比。通过重复此过程K次(每次折叠一次),我们将为整个训练数据集生成元数据。下图描述了该过程。最终结果是整个数据集的一组元数据,其中元数据是根据样本外数据生成的(从基础学习器的角度来看,是针对每个折叠):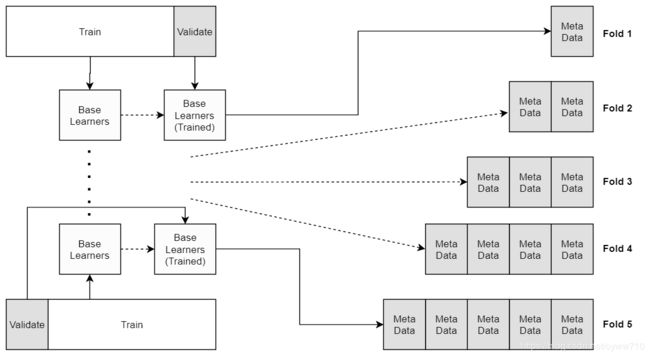
堆叠取决于基础学习器的多样性。如果基础学习器在问题的整个领域表现出相同的特征和表现,那么元学习器将很难显着提高他们的集体表现。此外,将需要一个复杂的元学习器。如果基础学习器本身是多样化的,并且在问题的不同领域表现出不同的绩效特征,那么即使是简单的元学习器也将能够极大地提高他们的集体表现。混合使用不同的学习算法通常是一个好主意,以便捕获特征本身以及目标变量之间的线性和非线性关系。
通常,元学习器应该是一种相对简单的机器学习算法,以避免过度拟合。此外,应采取其他步骤以正规化元学习器。例如,如果使用决策树,则应限制树的最大深度。如果使用回归模型,则应首选正则化回归(例如弹性网或岭回归)。如果需要更复杂的模型以提高整体的预测性能,则可以使用多级堆栈,其中,随着堆栈级别的增加,模型的数量和每个模型的复杂性都会降低

元学习器的另一个真正重要的特征应该是能够处理相关的输入,尤其是像朴素的贝叶斯分类器那样,不对特征彼此之间的独立性做出任何假设。如果元学习器(元数据)的输入将高度相关, 发生这种情况是因为所有基础学习器都受过训练以预测相同的目标。因此,他们的预测将来自相同函数的近似值。尽管预测值会有所不同,但它们会彼此接近。
尽管scikit-learn确实可以实现大多数集成方法,但堆栈并不是其中一种。下面我们会提供回归和分类问题中怎么用Python实现堆叠技术。
堆叠
- 回归问题
- 分类问题
- 写stacking的模块
回归问题
加载模块
from sklearn.datasets import load_diabetes
from sklearn.neighbors import KNeighborsRegressor
from sklearn.tree import DecisionTreeRegressor
from sklearn.linear_model import LinearRegression, Ridge
from sklearn.model_selection import KFold
from sklearn import metrics
import numpy as np
生成训练测试集
diabetes = load_diabetes()
train_x, train_y = diabetes.data[:400], diabetes.target[:400]
test_x, test_y = diabetes.data[400:], diabetes.target[400:]
创建基础学习器(base-learner)和元学习器(meta-learner)
## 基础学习器
base_learners = []
knn = KNeighborsRegressor(n_neighbors=5)
base_learners.append(knn)
dtr = DecisionTreeRegressor(max_depth=4 , random_state=123456)
base_learners.append(dtr)
ridge = Ridge()
base_learners.append(ridge)
## 元学习器
meta_learner = LinearRegression()
初始化学习者之后,我们需要为训练集创建元数据。通过首先用KFold(n_splits = 5)指定分割数(K),然后调用KF.split(train_x),将训练集分成五个。反过来,这将返回生成训练集的五个分段的训练和测试索引。对于这些每个拆分,我们使用train_indices(四个folds)指示的数据来训练我们的基础学习器,并在与test_indices相对应的数据上创建元数据。此外,我们将每个分类器的元数据存储在meta_data数组中,并将相应的目标存储在meta_targets数组中。最后,我们转置meta_data以获得(实例,特征)形状。
在训练集创建元数据集(meta-data)
# Create variables to store metadata and their targets
meta_data = np.zeros((len(base_learners), len(train_x)))
meta_targets = np.zeros(len(train_x))
meta_data.shape
(3, 400)
# Create the cross-validation folds
KF = KFold(n_splits=5)
meta_index = 0
for train_indices, test_indices in KF.split(train_x):
for i in range(len(base_learners)):
learner = base_learners[i]
learner.fit(train_x[train_indices], train_y[train_indices])
predictions = learner.predict(train_x[test_indices])
meta_data[i][meta_index:meta_index+len(test_indices)] = predictions
meta_targets[meta_index:meta_index+len(test_indices)] = train_y[test_indices]
meta_index += len(test_indices)
# Transpose the metadata to be fed into the meta-learner
meta_data = meta_data.transpose()
meta_data
array([[221. , 186.46031746, 179.44148461],
[ 83.2 , 91.72477064, 94.56884758],
[134.4 , 186.46031746, 165.29144916],
...,
[204.6 , 168.23076923, 160.66683682],
[117.4 , 168.23076923, 156.86271927],
[212. , 168.23076923, 176.6069636 ]])
对于测试集,我们不需要将其拆分为折叠。我们仅在整个训练集上训练基础学习器,并在测试集上进行预测。此外,我们评估每个基础学习者并存储评估指标,以将其与整体表现进行比较。
在测试集创建元数据集
# Create the metadata for the test set and evaluate the base learners
test_meta_data = np.zeros((len(base_learners), len(test_x)))
base_errors = []
base_r2 = []
for i in range(len(base_learners)):
learner = base_learners[i]
learner.fit(train_x, train_y)
predictions = learner.predict(test_x)
test_meta_data[i] = predictions
err = metrics.mean_squared_error(test_y, predictions)
r2 = metrics.r2_score(test_y, predictions)
base_errors.append(err)
base_r2.append(r2)
test_meta_data = test_meta_data.transpose()
现在,我们已经有了训练集和测试集的元数据集,我们可以在训练集上训练元学习器并在测试集上进行评估
# Fit the meta-learner on the train set and evaluate it on the test set
meta_learner.fit(meta_data, meta_targets)
ensemble_predictions = meta_learner.predict(test_meta_data)
err = metrics.mean_squared_error(test_y, ensemble_predictions)
r2 = metrics.r2_score(test_y, ensemble_predictions)
# Print the results
print('ERROR R2 Name')
print('-'*20)
for i in range(len(base_learners)):
learner = base_learners[i]
print(f'{base_errors[i]:.1f} {base_r2[i]:.2f} {learner.__class__.__name__}')
print(f'{err:.1f} {r2:.2f} Ensemble')
ERROR R2 Name
--------------------
2697.8 0.51 KNeighborsRegressor
3142.5 0.43 DecisionTreeRegressor
2564.8 0.54 Ridge
2066.6 0.63 Ensemble
显而易见,与最佳基础学习者相比,r平方改善了16%以上(岭回归),而MSE改善了近20%。这是一个很大的改进
分类问题
加载模块
from sklearn.datasets import load_breast_cancer
from sklearn.neighbors import KNeighborsClassifier
from sklearn.tree import DecisionTreeClassifier
from sklearn.neural_network import MLPClassifier
from sklearn.naive_bayes import GaussianNB
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import KFold
from sklearn import metrics
import numpy as np
创建训练集和测试集
bc = load_breast_cancer()
train_x, train_y = bc.data[:400], bc.target[:400]
test_x, test_y = bc.data[400:], bc.target[400:]
下面我们初始化生成基础学习器和元学习器。其中MLPClassifier具有100个神经元的单层
初始化基础学习器和元学习器
## 基础学习器
base_learners = []
knn = KNeighborsClassifier(n_neighbors=2)
base_learners.append(knn)
dtr = DecisionTreeClassifier(max_depth=4, random_state=123456)
base_learners.append(dtr)
mlpc = MLPClassifier(hidden_layer_sizes =(100, ),
solver='lbfgs', random_state=123456)
base_learners.append(mlpc)
## 元学习器
meta_learner = LogisticRegression(solver='lbfgs')
在训练集创建元数据集(meta-data)
meta_data = np.zeros((len(base_learners), len(train_x)))
meta_targets = np.zeros(len(train_x))
# Create the cross-validation folds
KF = KFold(n_splits=5)
meta_index = 0
for train_indices, test_indices in KF.split(train_x):
for i in range(len(base_learners)):
learner = base_learners[i]
learner.fit(train_x[train_indices], train_y[train_indices])
predictions = learner.predict_proba(train_x[test_indices])[:,0]
meta_data[i][meta_index:meta_index+len(test_indices)] = predictions
meta_targets[meta_index:meta_index+len(test_indices)] = train_y[test_indices]
meta_index += len(test_indices)
# Transpose the metadata to be fed into the meta-learner
meta_data = meta_data.transpose()
在测试集创建元数据集
test_meta_data = np.zeros((len(base_learners), len(test_x)))
base_acc = []
for i in range(len(base_learners)):
learner = base_learners[i]
learner.fit(train_x, train_y)
predictions = learner.predict_proba(test_x)[:,0]
test_meta_data[i] = predictions
acc = metrics.accuracy_score(test_y, learner.predict(test_x))
base_acc.append(acc)
test_meta_data = test_meta_data.transpose()
训练模型打印结果
# Fit the meta-learner on the train set and evaluate it on the test set
meta_learner.fit(meta_data, meta_targets)
ensemble_predictions = meta_learner.predict(test_meta_data)
acc = metrics.accuracy_score(test_y, ensemble_predictions)
# Print the results
print('Acc Name')
print('-'*20)
for i in range(len(base_learners)):
learner = base_learners[i]
print(f'{base_acc[i]:.2f} {learner.__class__.__name__}')
print(f'{acc:.2f} Ensemble')
Acc Name
--------------------
0.86 KNeighborsClassifier
0.88 DecisionTreeClassifier
0.23 MLPClassifier
0.91 Ensemble
写stacking的模块
我们可以把之前的code总结一下然后写成新的模块重复使用
import numpy as np
from sklearn.model_selection import KFold
from copy import deepcopy
class StackingRegressor():
def __init__(self, learners):
# Create a list of sizes for each stacking level And a list of deep copied learners
self.level_sizes = []
self.learners = []
for learning_level in learners:
self.level_sizes.append(len(learning_level))
level_learners = []
for learner in learning_level:
level_learners.append(deepcopy(learner))
self.learners.append(level_learners)
# Creates training meta data for every level and trains each level on the previous level's meta data
def fit(self, x, y):
# Create a list of training meta data, one for each stacking level
# and another one for the targets. For the first level, the actual data
# is used.
meta_data = [x]
meta_targets = [y]
for i in range(len(self.learners)):
level_size = self.level_sizes[i]
# Create the meta data and target variables for this level
data_z = np.zeros((level_size, len(x)))
target_z = np.zeros(len(x))
train_x = meta_data[i]
train_y = meta_targets[i]
# Create the cross-validation folds
KF = KFold(n_splits=5)
meta_index = 0
for train_indices, test_indices in KF.split(x):
# Train each learner on the K-1 folds and create
# meta data for the Kth fold
for j in range(len(self.learners[i])):
learner = self.learners[i][j]
learner.fit(train_x[train_indices], train_y[train_indices])
predictions = learner.predict(train_x[test_indices])
data_z[j][meta_index:meta_index+len(test_indices)] = predictions
target_z[meta_index:meta_index+len(test_indices)] = train_y[test_indices]
meta_index += len(test_indices)
# Add the data and targets to the meta data lists
data_z = data_z.transpose()
meta_data.append(data_z)
meta_targets.append(target_z)
# Train the learner on the whole previous meta data
for learner in self.learners[i]:
learner.fit(train_x, train_y)
# The predict function. Creates meta data for the test data and returns
# all of them. The actual predictions can be accessed with meta_data[-1]
def predict(self, x):
# Create a list of training meta data, one for each stacking level
meta_data = [x]
for i in range(len(self.learners)):
level_size = self.level_sizes[i]
data_z = np.zeros((level_size, len(x)))
test_x = meta_data[i]
# Create the cross-validation folds
KF = KFold(n_splits=5)
for train_indices, test_indices in KF.split(x):
# Train each learner on the K-1 folds and create
# meta data for the Kth fold
for j in range(len(self.learners[i])):
learner = self.learners[i][j]
predictions = learner.predict(test_x)
data_z[j] = predictions
# Add the data and targets to the meta data lists
data_z = data_z.transpose()
meta_data.append(data_z)
# Return the meta_data the final layer's prediction can be accessed
# With meta_data[-1]
return meta_data
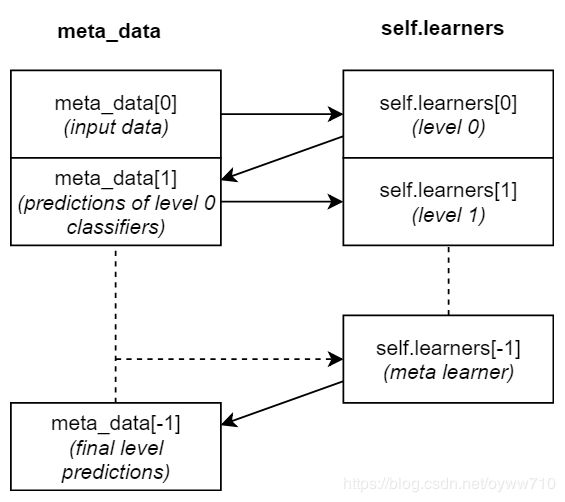
其中的图示是
然后我们可以来直接调用上面写的模块了
diabetes = load_diabetes()
train_x, train_y = diabetes.data[:400], diabetes.target[:400]
test_x, test_y = diabetes.data[400:], diabetes.target[400:]
base_learners = []
knn = KNeighborsRegressor(n_neighbors=5)
base_learners.append(knn)
dtr = DecisionTreeRegressor(max_depth=4, random_state=123456)
base_learners.append(dtr)
ridge = Ridge()
base_learners.append(ridge)
meta_learner = LinearRegression()
# Instantiate the stacking regressor
sc = StackingRegressor([[knn,dtr,ridge],[meta_learner]])
# Fit and predict
sc.fit(train_x, train_y)
meta_data = sc.predict(test_x)
# Evaluate base learners and meta-learner
base_errors = []
base_r2 = []
for i in range(len(base_learners)):
learner = base_learners[i]
predictions = meta_data[1][:,i]
err = metrics.mean_squared_error(test_y, predictions)
r2 = metrics.r2_score(test_y, predictions)
base_errors.append(err)
base_r2.append(r2)
err = metrics.mean_squared_error(test_y, meta_data[-1])
r2 = metrics.r2_score(test_y, meta_data[-1])
# Print the results
print('ERROR R2 Name')
print('-'*20)
for i in range(len(base_learners)):
learner = base_learners[i]
print(f'{base_errors[i]:.1f} {base_r2[i]:.2f} {learner.__class__.__name__}')
print(f'{err:.1f} {r2:.2f} Ensemble')
ERROR R2 Name
--------------------
2697.8 0.51 KNeighborsRegressor
3142.5 0.43 DecisionTreeRegressor
2564.8 0.54 Ridge
2066.6 0.63 Ensemble
和之前分步做的结果一样。
总的来说堆叠可以包含许多层次。每个级别都会为下一个级别生成元数据。应该通过将训练集划分为K折并在K-1上迭代训练,同时为第Kth折创建元数据来创建每个级别的元数据。创建元数据后,应该在整个训练集中训练当前级别。**基础学习器必须多样化。**元学习器应该是一个相对简单的算法,可以防止过度拟合。如果可能,请尝试在元学习器中引入正则化。例如,如果使用决策树,请限制最大深度。元学习器应该能够相对较好地处理相关的输入。