LR(0), SLR(1)到LR(1)语法分析详解
今天讲解LR(0)SLR(1)LR(1)
伪代码
rust实现LALR(1) 我觉得实现LR(1)就够了, lalr(1)反而是负担
- 首先是
自底向上分析过程:为一个输入串构造语法分析树的过程 - LR(k)分析技术:
- L:从左向右
- R: 反向构造一个最右推导序列
- k: 做出语法分析决定时向前看k个输入符号
- 当然在实践中我们只考虑
k=0或k=1的情况
为啥要用LR语法分析器呢? LL不香吗?
- 几乎所有的程序语言, 只要能写出改语言的
上下文无关文法, 就可以构造出相应的LR语法分析器. - LR无回溯, 很高效. @算符优先
- LR(k)分析能力强于LL(k)
- 总结一下. LR分析的优点
- 高性能
- 高能力
- 使用范围广
- 可自动生成
当然LR的缺点也是有的.
是时候拿出万年老二if c1 then if c2 then e2 else e3来抬杠了.
但我们可以稍微改写成if c1 { if c2 {e2 } else {e3}}.
还有手写LR分析是火葬场. 就比如我写的一个lalr分析器.
既然LR是移近归约分析器. 那何时移近, 何时归约?
移近&归约
我们通过维护一些状态, 来指导我们做出移近或归约的决定.
哦? 状态???
我们通过 A → X . Y Z A \rightarrow X.YZ A→X.YZ中点的位置来表示当下状态.
点左边的是可以由 X X X推导得到的串, 点右边是接下来想看到一个能从 Y Z YZ YZ推导得到的串.
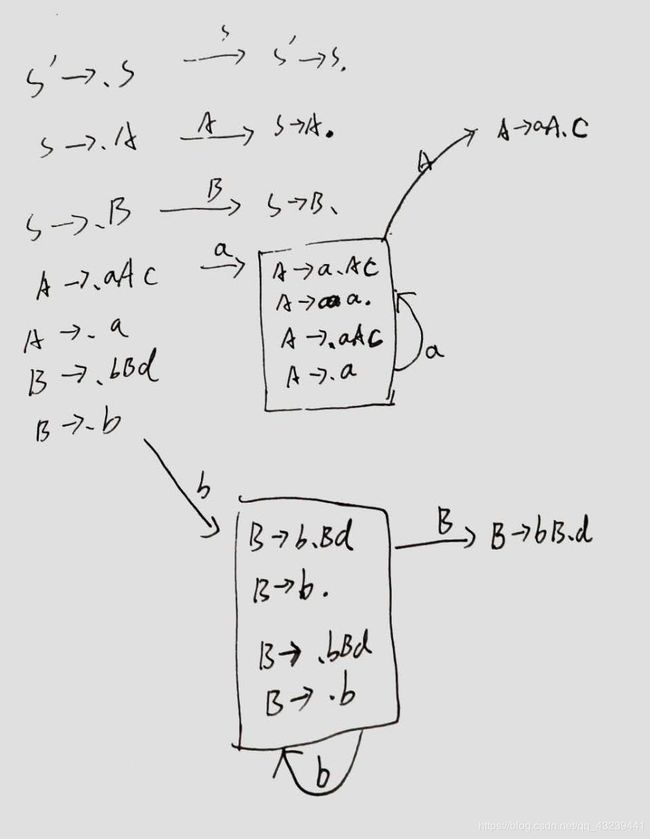
用状态的思想我们可以得出LR(0)自动机, 如图所示的例子
这是一个自动机呀!
为啥可以使用LR(0)自动机来做出移近/归约决定?
因为LR(0)自动机可以刻画出可能出现在分析器栈中的文法符号串.
即LR(0)自动机能识别可行前缀
对于一个可行前缀, 但前面有多条路怎么选?
可以查看下一个输入符号来解决.
SLR(1)出现了!
SLR(1)与LR(0)的不同在于:
-
LR(0)
- if A → α . A \rightarrow \alpha. A→α.
- for b in T: //T为终结符集合(包括结束符
#)- Action[i,b]=Reduce A → α . A \rightarrow \alpha. A→α.
- for b in T: //T为终结符集合(包括结束符
- if A → α . A \rightarrow \alpha. A→α.
-
SLR(1)
- if A → α . A \rightarrow \alpha. A→α.
- for b in FOLLOW(A):
- Action[i,b]=Reduce A → α . A \rightarrow \alpha. A→α.
- for b in FOLLOW(A):
- if A → α . A \rightarrow \alpha. A→α.
SLR(1)的FOLLOW(A)一把梭就可以解决问题了吗?
如何可以该多好, 可惜不行.
比如以下文法SLR(1)就不能识别
S → L = R ∣ R S\rightarrow L=R | R S→L=R∣R
L → ∗ R ∣ i d L \rightarrow *R |id L→∗R∣id
R → L R \rightarrow L R→L
FOLLOW(L) = FOLLOW( R ) = {#,=}
对于 L . = R L.=R L.=R来说, 下一步动作有 归 约 R → L . 归约R \rightarrow L. 归约R→L.或者 移 进 S → L . = R 移进S \rightarrow L.=R 移进S→L.=R. 然而我们没有以 R = . . . R=... R=...开头的句型.
FOLLOW集还是不够精细.
说明我们的SLR(1)自动机无法处理该文法. 但左值右值又常用.
所以我们需要更为精细的操作.
LR(1)出现了!
只有在形如 [ A → α . , a ] [A \rightarrow \alpha. ,a] [A→α.,a]的项且下一个输入符号为a的情况下, 我们才会按照 A → α A \rightarrow \alpha A→α进行归约.
那如何计算下一个符号a呢?
是时候召唤龙书了!
 这里重点看
这里重点看GOTO函数中将 [ A → α X . β , a ] 加 入 J 中 [A\rightarrow \alpha X. \beta, a]加入J中 [A→αX.β,a]加入J中.
我们的向前看符号通过GOTO函数实现了传播.
LR(1)的问题呢?
重复项实在是太多了. LALR(1)也不少
虽然文法很nb,但是实践中空间开销过大.
压缩一下?
咋压缩?
从LR(1)项 [ A → α X . β , a ] [A\rightarrow \alpha X. \beta, a] [A→αX.β,a]中的向后看符a入手, 如何尽可能合并, 而且不带来新的冲突.
就可以降低空间开销.
用LALR(1)来代替LR(1). 虽然损失了分析能力 ,但是对于常见语言还是的.
LALR(1)有些复杂, 可以单开一篇文章讲解.
欲听后事如何, 请听下回分解.
参考
- 龙书