python数据结构与算法 1 栈的实现与应用

Python 数据结构与算法1(栈)

线性结构

什么是线性结构？
1线性结构是一种有数据项的集合,其中每个数据项都有唯一的前驱和后继。除了第一个没有前驱，最后一个没有后继。新的数据项加入到数据集中是，只会加入到原有某个数据项之前或之后。具有这种性质的数据集，就称为线性结构
2线性结构总有两端，在不同的情况下，两端的称呼也不相同，有时候称为“左”“右”端、“前”“后”端、“顶”“底”端
3两端的称呼并不是关键，不同线性结构的关键区别在于数据项增减的方式有的结构只允许数据项中一端增加，而有的结构则允许数据项从两端移除

栈

什么是栈？
1栈是一种有次序的数据项集合，在栈中，数据项的加入和移除都仅发生在同一端，一端叫栈＂顶ｔｏｐ＂，另一端叫栈＂底ｂａｓｅ＂
２日常生活中有很多栈的应用，盘子，托盘，书堆等等

３距离栈底越近的数据项，留在栈中的时间就越长，而最新加入栈的数据项就会被最先移除
４这种次序通常称为＂后近先出ＬＩＦＯ：last in First out, 这是一种基于数据项保存时间的次序,时间越短的离栈顶越近,而时间越长的离栈底越近

栈的特性

反转次序:这种访问次序反转的特性,我们在某些计算机操作上碰到过
浏览器的"后退back"按钮,最先返回的是最近返回的网页

ADT 栈

抽象数据类型Stack: 抽象数据类型"栈"是一个有次序的数据集,每个数据项仅从"栈顶"一端加入到数据集中，栈具有后进先出LIFO的特性
栈的定义如下

Stack（）创建一个空栈，不包含任何数据项
push（item）：将item加入栈顶，无返回值
pop（）：将栈顶数据项移除，并返回，栈被修改
peek（）：”窥视“栈顶数据项，返回栈顶的数据项但不移除，栈不被修改
isEmpty（）：返回栈是否为空栈
size（）：返回栈中有多少个数据项

用Python 实现ADT Stack
我们可以用Python中list来实现,可以将list的任意一端设置为栈顶
在此,我们选用list的末端作为栈顶,就可以通过对list的append和pop来实现,非常简单

class Stack:
    def __init__(self):
        self.items = []
    def isEmpty(self):
        return self.items==[]
    def size(self):
        return len(self.items)
    def pop(self):
        return self.items.pop()
    def push(self,item):
        self.items.append(item)
    def peek(self):
        return self.items[-1]

栈的应用1简单括号匹配

在许多正文中都有括号，特别是在表示程序、数学表达式的正文片段里，括号有正确配对问题。下面考虑Python程序里的括号，在这里可以看到：

• 存在多种不同的括号，下面只考虑其中三种：园括号、方括号和花括号
• 每种括号都包括一个开括号和一个闭括号。括号扩起的片段可能嵌套，各种括号应该正确地嵌套并分别配对

在扫描正文过程中，遇到的闭括号应该与此前最近遇到且尚未获得匹配的开括号配对。如果最近的未匹配开括号与当前闭括号不配对，或者找不到这样的开括号，就是匹配失败，说明这段正文里的括号不配对

由于存在不同的括号对，每种括号都可能出现任意多次，而且还可能嵌套。为了检查是否匹配，扫描中必须保存遇到的开括号。由于写程序时无法预知要处理的正文里会有多少括号需要保存，因此不能用固定数目变量保存，必须用缓存结构
由于括号的出现可能嵌套，需要逐对匹配：当前闭括号应该与前面最近的尚未匹配对的开括号匹配，下一个闭括号应与前面次近的括号匹配。这说明，需要存储的开括号的使用原则是后存入者先使用，符合LIFO原则
通过上面的分析，处理这个问题的脉络已经很清楚了：

• 顺序扫描被检查正文（一个字符串）里的一个个字符
• 检查中跳过无关字符（所有非括号字符都与当前处理无关）
• 遇到开括号是将其压入栈
• 与到闭括号时弹出当时的栈顶元素与之匹配
• 如果匹配成果则继续，发现不匹配时检查以失败结束

def matches(open,close):
    opens='([{'
    closers=')]}'
    return opens.index(open)==closers.index(close)

def kuohaopipei(symbolString):
    s = Stack()
    a = 0
    for i in symbolString:#遍历字符串
        if i  in '([{':#左括号入栈
            s.push(i)
        elif i in ')]}' and s.size()>0:#右括号且此时栈里有左括号,匹配则继续,不匹配退出循环
            if matches(s.pop(),i):
                continue
            else:
                a =1
                break
        elif i in ')]}' and s.size()<0:#有右括号,但此时栈里面已经没有左括号,退出循环,匹配失败
            a = 1
            break
    if a == 1:
        print("匹配失败")
    else:
        print('匹配成功')

栈的应用2 n进制转换为二进制

以十进制为例，十进制转换为2进制，每次得到的余数就是由低到高的二进制位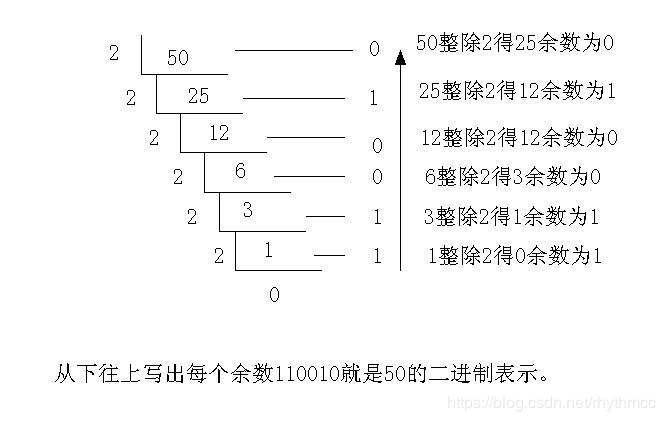
‘除以2’的过程，得到的余数是从低到高的次序，而输出则是从高到低，所以需要一个栈来反转次序
而十六进制的十六个不同数字则是0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F

def my_fc(my_number,n):#数字与进制
    s = Stack()
    digit = '0123456789ABCDEF'
    my_string=''
    while my_number:
        a=my_number%n
        s.push(a)
        my_number = my_number//n
    length = s.size()
    for i in range(length):
        my_string= my_string + digit[s.pop()]
    print(my_string)
my_fc(15,16)
my_fc(15,2)

栈的应用3表达式的表示、计算和变换

数学表达式中最重要的构造符号是一组二元运算符。在最常见表达式形式中，二元运算符写在其两个运算对象中间，这种写法称为中缀表达式。假设每个运算符的元数（运算对象个数）确定且唯一。在描述表达式时，最重要的问题是要准确描述计算的顺序。中缀表达式的主要缺点就在这里：它不足以表示所有可能的运算顺序，需要通过辅助符号、约定和/或辅助描述机制

首先，必须为中缀表达式引进括号的概念，规定括号里的运算先做（这是一种显示描述计算顺序的机制），以便于人们直接说明一些计算的特性顺序。写出所需的所有括号，有时会非常麻烦。为了缓解这种麻烦，人们又引进了优先级的概念，给各种运算符规定了不同的优先级（如先乘除后加减），规定优先级高的运算符结核性强，多个运算符相机出现时，优先级高的运算先做。有了这些还不够，还要规定具有相同优先级的运算符相继出现时的计算顺序（运算符的结合性）
而事实上，数学的表达式并不一定采用这种习惯写法，例如，可以采用纯粹的前缀表示， 这样写出的表达式称为前缀表达式。还有一种写法称为后缀表达式其中所有的运算符都写在它们的运算对象之后，这样写出的表达式称为后缀表达式
而前缀表达形式样儿后缀表达形式都不需要引进括号，也不需要任何有关优先级或结合性的规定， 已自然地描述任意复杂的表达式计算顺序：对于前缀表示，每个运算符的运算对象，就是它后面出现得几个完整表达式，表达式个数由运算符的元数确定。对于后缀表示，情况类似但位置相反

中缀表达式	前缀表达式	后缀表达式
A+B*C+D	++A*BCD	ABC*+D+
(A+B)*(C+D)	*+AB+CD	AB+CD+*
AB+CD	+ABCD	ABCD+
A+B+C+D	+++ABCD	AB+C+D+

后缀表达式的求值

在对后缀表达式从左到右扫描的过程中,由于操作符在操作数的后面,所以要暂存操作数,在碰到操作符的时候,再将暂存的两个操作数进行实际的计算
仍然是栈的特性:操作符只作用于离它最近的两个数
如"345±",我们先扫描到3、4、5，我们将它依次入栈，此时从栈顶到栈底为

栈
5
4
3

当扫描到”+“时，我们依次弹出x=5,y=4,y+x=9,此时将9压入栈

栈
9
3

此时扫描到"-",我们依次弹出x=9,y=3,y-x=-6,将-6压入栈
此时栈

栈
-6

为我们所要的答案

def domath(a,b,i):
    if i== '*':
        return a*b
    if i == '-':
        return a - b
    if i == '+':
        return a + b
    if i == '/':
        return a / b

def qiuzhi(num_string):
    s = Stack()
    for i in num_string:
        if i in '0123456789':
            s.push(i)
        if i in '+-*/':
            x=s.pop()
            y=s.pop()
            c=domath(int(y),int(x),i)#此时y在前,x在后
            s.push(c)
    return s.peek()

print(qiuzhi('2435-+/-'))

前缀表达式的求值

我们通过后缀表达式的求值,只要从后面遍历,类比就可以得到代码

def domath(a,b,i):
    if i== '*':
        return a*b
    if i == '-':
        return a - b
    if i == '+':
        return a + b
    if i == '/':
        return a / b

def qiuzhi(num_string):
    s = Stack()

    for i in num_string[::-1]:
        if i in '0123456789':
            s.push(i)
        if i in '+-*/':
            x=s.pop()
            y=s.pop()
            c=domath(int(x),int(y),i) #此时x在前,y在后
            s.push(c)
    return s.peek()

print(qiuzhi('-+341'))

中缀表达式转换为后缀表达式

中缀表达式中运算符处理比较麻烦:扫描中遇到一个运算符时,不能将其输出,只有看到下一运算符的优先级不高于本运算符时,才能去做本运算符要求的计算,或说这是才应该把本运算符送入后缀表达式

算法流程:

• 如果单词是操作数,则直接添加到后缀表达式列表的末尾
• 如果单词是左括号"(",则压入栈顶
• 如果单词是右括号")",则反复弹出栈顶操作符,加入到输出列表末尾,直到碰到左括号
• 如果单词是操作符"*/±",则压入栈顶(但在压入之前,要比较其与栈顶操作符的优先级如果栈顶的高于或等于它,就要反复弹出栈顶操作符,加入到输出列表末尾直到栈顶的操作符优先级低于他)
• 中缀表达式单词列表扫描结束后,把栈依次弹出输出到列表末尾
• 将列表用join方法合并为后缀表达式

def trans(num_):
    s = Stack()
    li_=[]
    rank_={}
    rank_['*'] = 3
    rank_['/'] = 3
    rank_['+'] = 2
    rank_['-'] = 2
    rank_['('] = 1
    b=1
    for i in num_:
        if i in '0123456789':
            li_.append(i)
        if i =='(':
            s.push(i)
        elif i ==')':
            while b:
                b = s.pop()
                if b != '(':
                    li_.append(b)
                else:
                    break
        elif i in "*/+-" :
            if s.isEmpty():
                s.push(i)
            else:
                while rank_[s.peek()] >=rank_[i] :
                    li_.append(s.pop())
                    if s.size()==0:
                        break
                s.push(i)


    while s.size():
        li_.append(s.pop())

    return "".join(li_)


print(trans("(1+2)*3/6"))