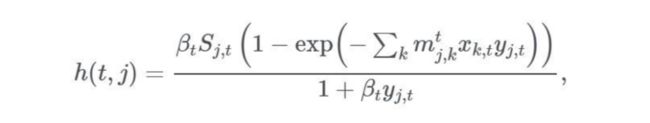新冠病毒在其他国家爆发会发生什么？Python 模拟告诉你结果

公众号关注 “GitHubDaily”

设为 “星标”，带你了解技术圈内新鲜事！

转自大数据文摘

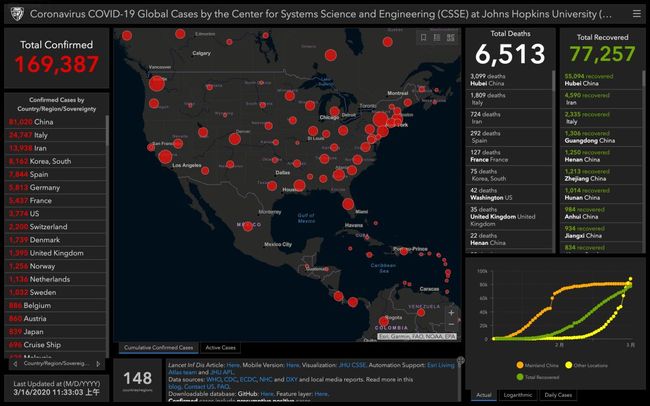
2019 年末，在中国武汉爆发的冠状病毒疫情冲击了整个金融市场和实体经济。这座总人口超过千万，春运期间流动人口超过 500 万的巨型城市的灾难在世界各地引发了一连串蝴蝶效应，也在全球普通民众中引发恐慌。

2020 年 1 月 30 日，2019-nCoV 已被世界卫生组织列为国际关注的突发公共卫生事件（PHEIC）。在撰写本文时，尚未发现经过医学研究验证的具体治疗方法。

此外，一些关键的流行病学指标，如基本再生数 (一个感染者传染的平均人数，即 R0 值) 仍然未知。当今时代，全球互联，这类流行病更是借势成为全球范围内的重大威胁之一。

可以推测，如果 2020 年全球发生灾难性事件 (大致定义为导致不少于 1 亿人伤亡的事件)，最有可能的原因恰恰是某种流行病 —— 而不是核灾难，也不是气候灾难，等等。全球范围内的快速城市化进一步加剧了这一问题，人口密集且频繁流动的城市俨然变成了疾病扩散网络的传播节点，使得防疫系统变得极为脆弱。

武汉的这场灾难也引发了全球对于城市规划和防疫政策的思考。如果疾病不是在武汉，而是在另一座人口规模更小、人口流动也更弱的城市，它的传染性和感染人数，又会是怎样的故事？

在这篇文章中，我们将讨论当流行病袭击一个城市时会发生什么，应该立即采取什么措施，以及这对城市规划、政策制定和管理有什么影响。

我们将以亚美尼亚首都，一个人口刚过百万、以钢铁和葡萄酒著名的城市埃里温市为例进行研究，建立数学模型并模拟冠状病毒在该市的传播，研究城市流动模式如何影响疾病的传播。

城市流动性

有效、高效和可持续的城市流动性对现代城市的运作至关重要。它已经被证明会直接影响城市的宜居性和经济产出 (GDP)。然而，一旦发生疫情，它就会火上浇油，扩大疾病的传播。

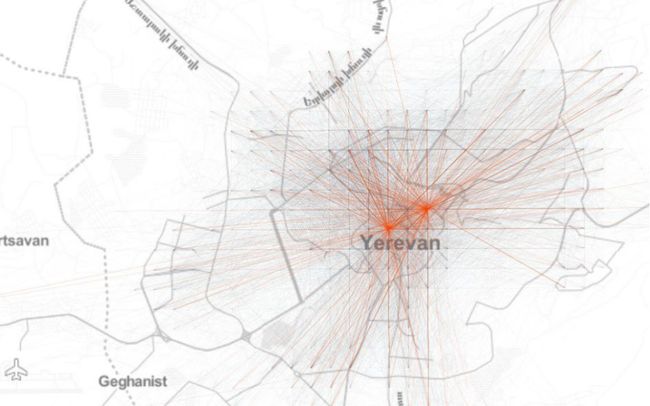
那么，让我们先来看看埃里温市在一个平面坐标系上的聚合 OD 流动网络 (Origin-Destination)，以了解城市流动模式的空间结构：

接着，如果我们观察网格的总流入量，我们会看到或多或少的单中心空间组织，其中一些网格的日流入量较高但位于中心之外:

现在，假设一种流行病在城市的任意地点爆发。它将如何传播？我们能做些什么来控制它？

流行病学建模

为了回答这些问题，我们将建立一个简单的房室模型来模拟传染病在城市中的传播。

当一种流行病爆发时，其传播动力会有显著变化，这取决于最初感染的地理位置及其与城市其他地区的连接性。这是最近关于城市人口流行病的数据驱动研究得出的最重要见解之一。然而，正如我们将在下文进一步看到的，各种结果都要求采取类似的措施来控制疫情，并在规划和管理城市时考虑到这种可能性。

注：compartmental model，房室模型，也称 SIR 模型，是一种简化的传染病数学模型。

由于我们的目标是展示城市流行病传播的一般原理，而不是建立一个实时的精确模型，我将参考《自然》杂志的一篇文章，通过简单地修改经典 SIR 模型即可满足我们的需求。

相关链接：

https://www.nature.com/articles/s41467-017-02064-4

这个模型把人口分成三部分。在时间 t 的每个位置 i，其三个房室如下：

• Si,t：尚未感染或易感的人数；

• Ii,t：感染疾病并有能力将疾病传播给易感人群的人数；

• Ri,t: 由于康复或者死亡，在被感染后从受感染组中移除的人数。这个群体中的个体没有能力再次感染该疾病或将感染病传染给他人。

在我们的模拟中，时间将是一个离散变量，因为系统的状态是以日为单位进行建模的。在 t 时刻 j 点的完全易感人群中，感染病出现的概率为：

βt 是 t 时刻的传输率；mj,k 是从 k 地到 j 地的流动性，xk,t 和 yk,t 代表 t 时刻 k 地和 j 地的感染和易感人群数，其中 xk,t = Ik,t / Nk，yj,t = Sj,t / Nj，Nk 和 Nj 代表 k 地和 j 地的人口总数。然后，我们继续模拟一个随机过程，将这种疾病引入完全易感人群所在的地区，其中 Ij,t+1 是概率为 h (t,j) 的伯努利随机变量。

一旦感染在随机地点出现，疾病不仅会在该地点传播，还会通过携带者传播到他处。这就是以 OD 流矩阵为特征的城市流动模式发挥关键作用的地方。

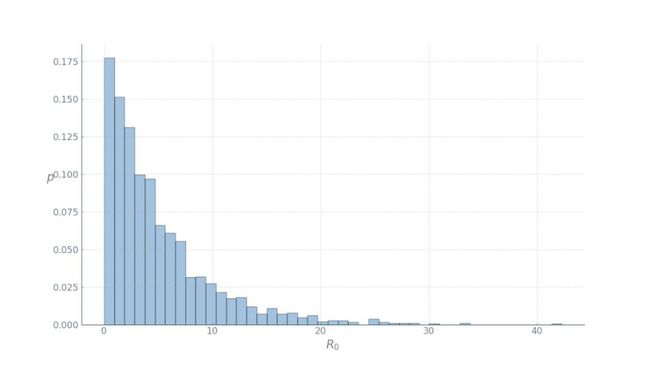
此外，为了确定疾病是如何通过感染者传播的，我们需要考虑其 R0 值。此处，其中 y 表示的是治愈率，也可以认为是二次感染率。在撰写本文时，新型冠状病毒的基本再生数估计值在 1.4 到 4 之间。凡事做最坏的准备，因此我们假设 R0 值为 4。需要注意的是，R0 值是一个有期望值的随机变量。为了让事情更有趣一点，我们在每个地区采用不同的 R0 值进行模拟，其中 R0 值服从均值为 4 的伽玛分布:

现在我们来讨论所建立的模型：

βk,t 是 t 时刻 k 地的转移率，α 是刻画出行方式倾向的参数。

上述的模型十分简洁：为了求得 t + 1 时刻的 j 地的尚未感染或易感的人数，我们需要从 t 时刻的 j 地的尚未感染或易感的人数中减去 j 地本地感染的人数（第一个方程的第二部分），还要减去从其他地方来到 j 地的感染者数，这些外来的感染者通过其传输率进行加权计算（第一个方程的第三部分）。由于总人口数 Nj = Sj + Ij + Rj，我们需要将减去的部分移至感染组，同时将治愈的部分移至 Rj,t+1 (第二个和第三个方程)。

仿真建立

在此分析中，我们将使用由当地共乘公司 gg 提供的 GPS 数据获得的一个典型日的总 OD 流量矩阵作为埃里温市交通模式的代表。

接下来，我们需要每个 250×250m 网格单元的人口计数，通过按比例缩放提取的流量计数来近似计算，从而使不同位置的总流入量之和接近埃里温市 110 万人口的一半。这是一个大胆的假设，但对结果影响不大。

减少公共交通？

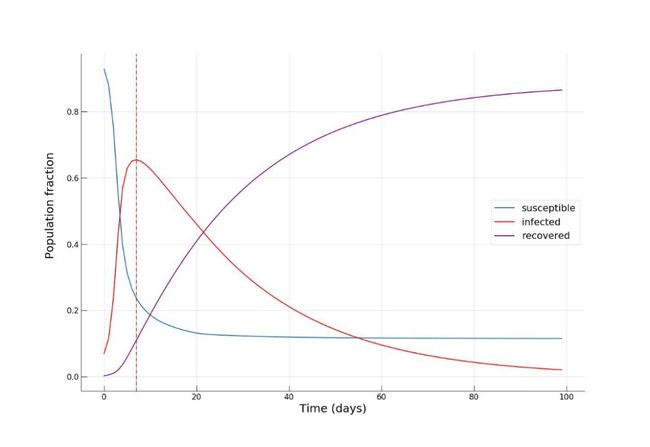
第一次模拟，我们将模拟背景设定为一个高度依赖公共交通的未来城市，设定流动率 α=0.9：

可以看到，经过大约 8-10 天左右的时间感染人数比例迅速增加至 70%，达到峰值，但此时仅有小部分（约 10%）的人康复。至 100 天时，疫情逐渐缓解，康复人数比例达到了惊人的 90%！现在，我们再来看一下如果将公共交通强度 α 降低至 0.2 时，是否有利于缓解传染病的传播。这可以解释为采取严厉措施来降低城市流动性（例如实施宵禁），或者增加私家车出行比例，以减少人们出行期间感染的机率。

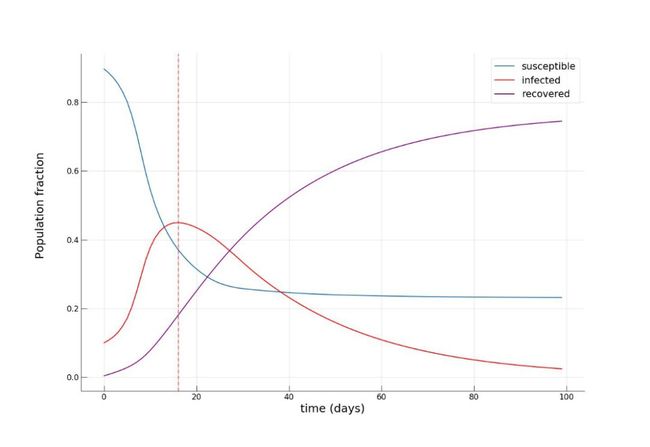
可以发现在这种假设下，疫情在 16 至 20 天左右到达顶峰，峰值感染人数比例明显降低（约 45%），并且此时康复人数为之前的两倍（约 20%）。在疫情结行将结束时，易感染人群比例也是之前的两倍（约 24% vs. 约 12%），这意味着更多的人躲过了这场疫情。正如人们所期望的，通过实施严厉的管控措施来临时降低城市的流动性对于减少传染病传播有明显作用。

隔离热门区域？

接着，再来看另一个直观想法 —— 隔离一些关键区域能否得到预期的效果。为了测试这一想法，先挑选人流量位于前 1% 的区域：

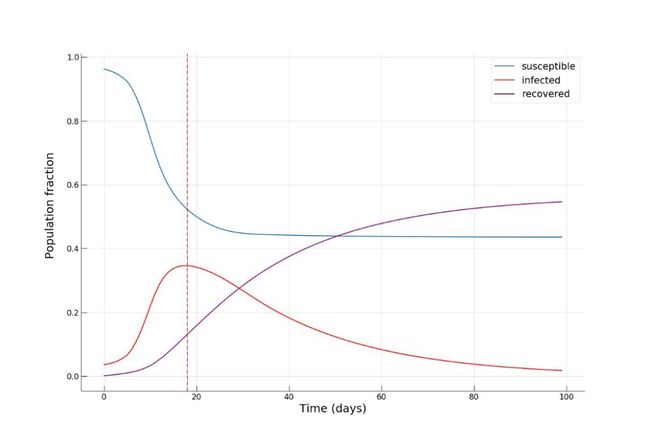
接着完全限制这些区域的进出，建立有效的隔离制度。从这张图我们可以看出，在埃里温市这些位置主要位于市中心，另两个位置是两家最大的购物商场。将 α 取中间值，即 0.5，我们得到如下结果：

感染人数比例的峰值更小了（约 35%），并且更重要的是，在疫情行将结束时，大约一半的人未被感染，说明该种方法能够帮助人们有效的降低感染风险！

如下动图显示了高度依赖公共交通场景下的结果：

结论

该实验绝不是说我们已经构建了准确的传染病模型（甚至模型中不涉及任何传染病学的基础知识），我们的目标是在传染病爆发时能够即时了解城市交通网络对传染病传播的影响。

随着人口密度、流动性和互动性的增强，我们的城市更容易发生 “黑天鹅” 事件，并且变得更加脆弱。例如，我们从这个模型可以发现在关键地区实施隔离制度或者采取严苛的措施来控制人员流动能够在疫情期间发挥巨大作用。

但还有一个十分重要的问题就是，如何在执行这些措施期间，使得城市功能和经济的损坏最小化？

此外，传染病传播机制也是一个活跃的研究领域，该领域的成果必须要渗透并整合到城市规划、政策制定和城市管理当中，以使我们的城市更安全更抗打击。

上述模型代码如下：

import numpy as np
  # initialize the population vector from the origin-destination flow matrix
  N_k = np.abs(np.diagonal(OD) + OD.sum(axis=0) - OD.sum(axis=1))
  locs_len = len(N_k)                 # number of locations
  SIR = np.zeros(shape=(locs_len, 3)) # make a numpy array with 3 columns for keeping track of the S, I, R groups
  SIR[:,0] = N_k                      # initialize the S group with the respective populations

  first_infections = np.where(SIR[:, 0]<=thresh, SIR[:, 0]//20, 0)   # for demo purposes, randomly introduce infections
  SIR[:, 0] = SIR[:, 0] - first_infections
  SIR[:, 1] = SIR[:, 1] + first_infections                           # move infections to the I group

  # row normalize the SIR matrix for keeping track of group proportions
  row_sums = SIR.sum(axis=1)
  SIR_n = SIR / row_sums[:, np.newaxis]

  # initialize parameters
  beta = 1.6
  gamma = 0.04
  public_trans = 0.5                                 # alpha
  R0 = beta/gamma
  beta_vec = np.random.gamma(1.6, 2, locs_len)
  gamma_vec = np.full(locs_len, gamma)
  public_trans_vec = np.full(locs_len, public_trans)

  # make copy of the SIR matrices 
  SIR_sim = SIR.copy()
  SIR_nsim = SIR_n.copy()

  # run model
  print(SIR_sim.sum(axis=0).sum() == N_k.sum())
  from tqdm import tqdm_notebook
  infected_pop_norm = []
  susceptible_pop_norm = []
  recovered_pop_norm = []
  for time_step in tqdm_notebook(range(100)):
      infected_mat = np.array([SIR_nsim[:,1],]*locs_len).transpose()
      OD_infected = np.round(OD*infected_mat)
      inflow_infected = OD_infected.sum(axis=0)
      inflow_infected = np.round(inflow_infected*public_trans_vec)
      print('total infected inflow: ', inflow_infected.sum())
      new_infect = beta_vec*SIR_sim[:, 0]*inflow_infected/(N_k + OD.sum(axis=0))
      new_recovered = gamma_vec*SIR_sim[:, 1]
      new_infect = np.where(new_infect>SIR_sim[:, 0], SIR_sim[:, 0], new_infect)
      SIR_sim[:, 0] = SIR_sim[:, 0] - new_infect
      SIR_sim[:, 1] = SIR_sim[:, 1] + new_infect - new_recovered
      SIR_sim[:, 2] = SIR_sim[:, 2] + new_recovered
      SIR_sim = np.where(SIR_sim<0,0,SIR_sim)
      # recompute the normalized SIR matrix
      row_sums = SIR_sim.sum(axis=1)
      SIR_nsim = SIR_sim / row_sums[:, np.newaxis]
      S = SIR_sim[:,0].sum()/N_k.sum()
      I = SIR_sim[:,1].sum()/N_k.sum()
      R = SIR_sim[:,2].sum()/N_k.sum()
      print(S, I, R, (S+I+R)*N_k.sum(), N_k.sum())
      print('\n')
      infected_pop_norm.append(I)
      susceptible_pop_norm.append(S)
      recovered_pop_norm.append(R)

相关报道：

https://towardsdatascience.com/modelling-the-coronavirus-epidemic-spreading-in-a-city-with-python-babd14d82fa2

推荐阅读：
GitHub 热榜：文字识别神器，超轻量级中文 OCR！

Unicode 发布新版本，「biáng biáng 面」马上可以打出来了！

牛逼了，日本神秘男子用 AI 黑科技破解马赛克，震惊业界大佬！

教你一招搞定 GitHub 下载加速！

卧槽！iPhone 上可以运行 Android 了？！