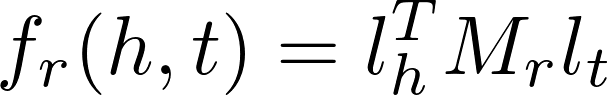知识图谱—知识表示

知识表示

1引言

传统的知识表示方法主要是以RDF(Resource Description Framework资源描述框架)的三元组SPO(subject,property,object)来符号性描述实体之间的关系。这种表示方法通用简单，受到广泛认可，但是其在计算效率、数据稀疏性等方面面临诸多问题。近年来，以深度学习为代表的以深度学习为代表的表示学习技术取得了重要的进展，可以将实体的语义信息表示为稠密低维实值向量，进而在低维空间中高效计算实体、关系及其之间的复杂语义关联，对知识库的构建、推理、融合以及应用均具有重要的意义。

2 代表模型

知识表示学习的代表模型有距离模型、单层神经网络模型、双线性模型、神经张量模型、矩阵分解模型、翻译模型等。

1）距离模型

距离模型提出了知识库中实体以及关系的结构化表示方法(structured embedding，SE)，其基本思想是：首先将实体用向量进行表示，然后通过关系矩阵将实体投影到与实体关系对的向量空间中，最后通过计算投影向量之间的距离来判断实体间已存在的关系的置信度。由于距离模型中的关系矩阵是两个不同的矩阵，使得协同性较差。

2）单层神经网络模型

针对上述提到的距离模型中的缺陷，提出了采用单层神经网络的非线性模型(single layer model，SLM)，模型为知识库中每个三元组（h,r,t) 定义了以下形式的评价函数：

式中， ut的T次幂∈R的k次幂为关系 r 的向量化表示；g()为tanh函数； Mr,1×Mr,2∈R的k次幂是通过关系r定义的两个矩阵。单层神经网络模型的非线性操作虽然能够进一步刻画实体在关系下的语义相关性，但在计算开销上却大大增加。

3）双线性模型

双 线 性 模 型 又 叫 隐 变 量 模 型 (latent factor model，LFM)。模型为知识库中每个三元组 定义的评价函数具有如下形式：

式中,Mr∈R的d×d次幂是通过关系r 定义的双线性变换矩阵；
lh×lt∈R的d次幂是三元组中头实体与尾实体的向量化表示。双线性模型主要是通过基于实体间关系的双线性变换来刻画实体在关系下的语义相关性。模型不仅形式简单、易于计算，而且还能够有效刻画实体间的协同性。基于上述工作，文献[45]尝试将双线性变换矩阵r M 变换为对角矩阵， 提出了DISTMULT模型，不仅简化了计算的复杂度，并且实验效果得到了显著提升。

4）神经张量模型

提出的神经张量模型，其基本思想是：在不同的维度下，将实体联系起来，表示实体间复杂的语义联系。模型为知识库中的每个三元组(h,r,t)定义了以下形式的评价函数：

式中， ut的T次幂∈R的k次幂为关系 r 的向量化表示；g()为tanh函数； Mr∈d×k×k是一个三阶张量；Mr,1×Mr,2∈R的k次幂是通过关系r定义的两个矩阵。

神经张量模型在构建实体的向量表示时，是将该实体中的所有单词的向量取平均值，这样一方面可以重复使用单词向量构建实体，另一方面将有利于增强低维向量的稠密程度以及实体与关系的语义计算。

5）矩阵分解模型

通过矩阵分解的方式可得到低维的向量表示，故不少研究者提出可采用该方式进行知识表示学习，其中的典型代表是提出的RESACL模型。在RESCAL模型中，知识库中的三元组集合被表示为一个三阶张量，如果该三元组存在，张量中对应位置的元素被置1，否则置为0。通过张量分解算法，可将张量中每个三元组（h,r,t)对应的张量值解为双线性模型中的知识表示形式lh的T次幂×Mr×lt并使|Xhrt-lh的T次幂×Mr×l|尽量小。

6）翻译模型

受到平移不变现象的启发，提出了TransE模型，即将知识库中实体之间的关系看成是从实体间的某种平移，并用向量表示。关系lr可以看作是从头实体向量到尾实体向量lt的翻译。对于知识库中的每个三元组(h,r,t),TransE都希望满足以下关系|lh+lt≈lt|：，其损失函数为：fr(h,t)=|lh+lr-lt|L1/L2, 该模型的参数较少，计算的复杂度显著降低。与此同时，TransE模型在大规模稀疏知识库上也同样具有较好的性能和可扩展性。

2.2 复杂关系模型

知识库中的实体关系类型也可分为1-to-1、1-to-N、N-to-1、N-to-N4种类型，而复杂关系主要指的是1-to-N、N-to-1、N-to-N的3种关系类型。由于TransE模型不能用在处理复杂关系上，一系列基于它的扩展模型纷纷被提出，下面将着重介绍其中的几项代表性工作。

1）TransH模型

提出的TransH模型尝试通过不同的形式表示不同关系中的实体结构，对于同一个实体而言，它在不同的关系下也扮演着不同的角色。模型首先通过关系向量lr与其正交的法向量wr选取某一个超平面F， 然后将头实体向量lh和尾实体向量lt法向量wr的方向投影到F, 最后计算损失函数。TransH使不同的实体在不同的关系下拥有了不同的表示形式，但由于实体向量被投影到了关系的语义空间中，故它们具有相同的维度。

2）TransR模型

由于实体、关系是不同的对象，不同的关系所关注的实体的属性也不尽相同，将它们映射到同一个语义空间，在一定程度上就限制了模型的表达能力。所以，提出了TransR模型。模型首先将知识库中的每个三元组(h, r,t)的头实体与尾实体向关系空间中投影，然后希望满足|lh+lt≈lt|的关系，最后计算损失函数。

提出的CTransR模型认为关系还可做更细致的划分，这将有利于提高实体与关系的语义联系。在CTransR模型中，通过对关系r 对应的头实体、尾实体向量的差值lh-lt进行聚类，可将r分为若干个子关系rc 。

3）TransD模型

考虑到在知识库的三元组中，头实体和尾实体表示的含义、类型以及属性可能有较大差异，之前的TransR模型使它们被同一个投影矩阵进行映射，在一定程度上就限制了模型的表达能力。除此之外，将实体映射到关系空间体现的是从实体到关系的语 义联系，而TransR模型中提出的投影矩阵仅考虑了不同的关系类型，而忽视了实体与关系之间的交互。因此，提出了TransD模型，模型分别定义了头实体与尾实体在关系空间上的投影矩阵。

4）TransG模型

提出的TransG模型认为一种关系可能会对应多种语义，而每一种语义都可以用一个高斯分布表示。TransG模型考虑到了关系r 的不同语义，使用高斯混合模型来描述知识库中每个三元组(h,r,t)头实体与尾实体之间的关系，具有较高的实体区分度。

5）KG2E模型

考虑到知识库中的实体以及关系的不确定性，提出了KG2E模型，其中同样是用高斯分布来刻画实体与关系。模型使用高斯分布的均值表示实体或关系在语义空间中的中心位置，协方差则表示实体或关系的不确定度。

知识库中，每个三元组(h,r,t)的头实体向量与尾实体向量间的

关系r可表示为：