R语言中的回归分析
1、简单线性回归分析
满足线性回归的几个要求:
用lm()拟合回归模型
lm(formula,data)
如何对拟合的结果进行评估?
(1)简单的线性回归的例子
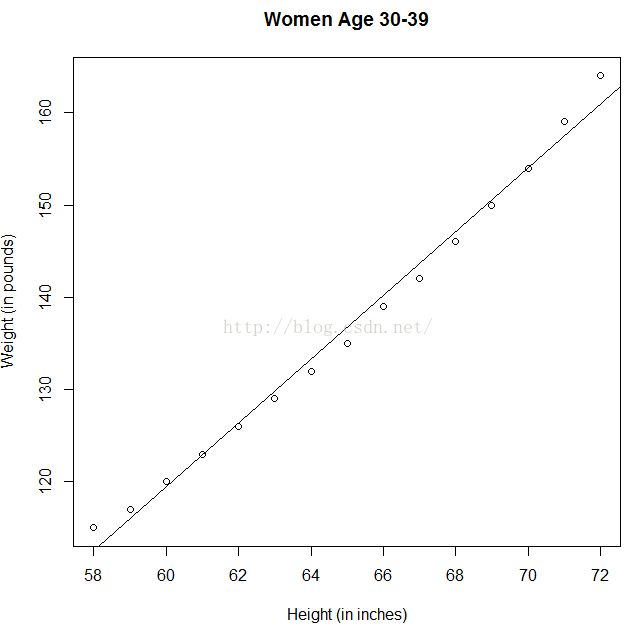
根据身高预测体重
fit <- lm(weight ~ height, data = women)
summary(fit)
Call:
lm(formula = weight ~ height, data = women)
Residuals:
Min 1Q Median 3Q Max
-1.7333 -1.1333 -0.3833 0.7417 3.1167
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -87.51667 5.93694 -14.74 1.71e-09 ***
height 3.45000 0.09114 37.85 1.09e-14 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 1.525 on 13 degrees of freedom
Multiple R-squared: 0.991, Adjusted R-squared: 0.9903
F-statistic: 1433 on 1 and 13 DF, p-value: 1.091e-14
women$weight
115 117 120 123 126 129 132 135 139 142 146 150 154 159 164
fitted(fit)
112.5833 116.0333 119.4833 122.9333 126.3833 129.8333 133.2833 136.7333
9 10 11 12 13 14 15
140.1833 143.6333 147.0833 150.5333 153.9833 157.4333 160.8833
residuals(fit)
1 2 3 4 5 6
2.41666667 0.96666667 0.51666667 0.06666667 -0.38333333 -0.83333333
7 8 9 10 11 12
-1.28333333 -1.73333333 -1.18333333 -1.63333333 -1.08333333 -0.53333333
13 14 15
0.01666667 1.56666667 3.11666667
plot(women$height, women$weight, main = "Women Age 30-39",
xlab = "Height (in inches)", ylab = "Weight (in pounds)")
abline(fit)
(2)多项式回归
fit2 <- lm(weight ~ height + I(height^2), data = women)
summary(fit2)
Call:
lm(formula = weight ~ height + I(height^2), data = women)
Residuals:
Min 1Q Median 3Q Max
-0.50941 -0.29611 -0.00941 0.28615 0.59706
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 261.87818 25.19677 10.393 2.36e-07 ***
height -7.34832 0.77769 -9.449 6.58e-07 ***
I(height^2) 0.08306 0.00598 13.891 9.32e-09 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.3841 on 12 degrees of freedom
Multiple R-squared: 0.9995, Adjusted R-squared: 0.9994
F-statistic: 1.139e+04 on 2 and 12 DF, p-value: < 2.2e-16
plot(women$height, women$weight, main = "Women Age 30-39",
xlab = "Height (in inches)", ylab = "Weight (in lbs)")
lines(women$height, fitted(fit2))
library(car)
scatterplot(weight ~ height, data = women, spread = FALSE,
lty.smooth = 2, pch = 19, main = "Women Age 30-39", xlab = "Height (inches)",
ylab = "Weight (lbs.)")
(3)多元线性回归
当预测变量不止一个时,简单线性回归就变成了多元线性回归
以基础包中的state.x77数据集为例,我们想探究一个州的犯罪率和其他因素的关系,包括人口、文盲率、平均收入和结霜天数(温度在冰点以下的平均天数)。
states <- as.data.frame(state.x77[, c("Murder", "Population",
"Illiteracy", "Income", "Frost")])
cor()函数提供了二变量之间的
相关系数
cor(states)
library(car)
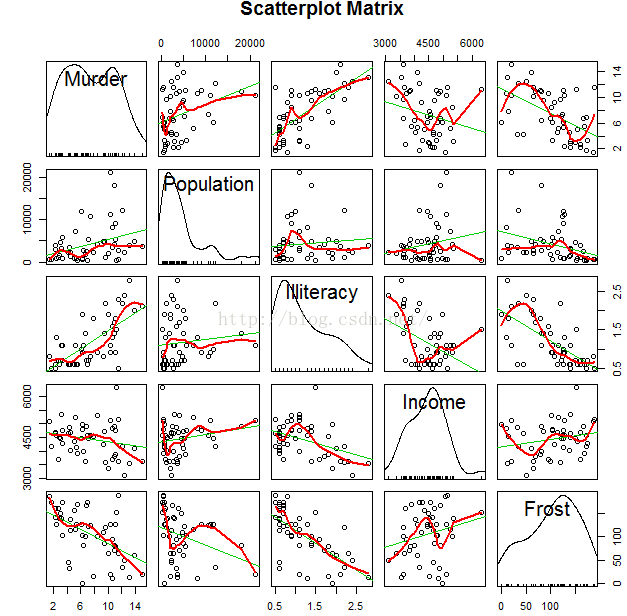
scatterplotMatrix()函数默认在非对角线区域绘制变量间的散点图,并添加平滑(loess)
和线性拟合曲线。对角线区域绘制每个变量的密度图和轴须图。
scatterplotMatrix(states, spread = FALSE, lty.smooth = 2,
main = "Scatterplot Matrix")
从上图可以看出:谋杀率是双峰的曲线,每个预测变量都一定程度上出现了偏斜。谋杀率随着人口和文盲率的增加而增加,随着收入水平和结霜天数增加而下降。同时,越冷的州府文盲率越低,收入水平越高。
fit <- lm(Murder ~ Population + Illiteracy + Income +
Frost, data = states)
summary(fit)
(4)有交互项的多元线性回归
使用mtcars数据集 考虑每公里跑的英里数与马力和车中以及二个变量之间的关系
fit <- lm(mpg ~ hp + wt + hp:wt, data = mtcars)
summary(fit)
Call:
lm(formula = mpg ~ hp + wt + hp:wt, data = mtcars)
Residuals:
Min 1Q Median 3Q Max
-3.0632 -1.6491 -0.7362 1.4211 4.5513
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 49.80842 3.60516 13.816 5.01e-14 ***
hp -0.12010 0.02470 -4.863 4.04e-05 ***
wt -8.21662 1.26971 -6.471 5.20e-07 ***
hp:wt 0.02785 0.00742 3.753 0.000811 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 2.153 on 28 degrees of freedom
Multiple R-squared: 0.8848, Adjusted R-squared: 0.8724
F-statistic: 71.66 on 3 and 28 DF, p-value: 2.981e-13
预测mpg的模型为mpg = 49.81 -0.12×hp - 8.22×wt + 0.03×hp×wt
library(effects)
plot(effect("hp:wt", fit, list(wt = c(2.2, 3.2, 4.2))),
multiline = TRUE)