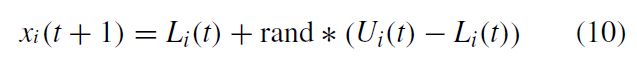论文研读-基于变量分类的动态多目标优化算法

论文研读-基于变量分类的动态多目标优化算法

A Dynamic Multiobjective Evolutionary Algorithm Based on Decision Variable Classification

觉得有用的话,欢迎一起讨论相互学习~

• 此篇文章为 Liang Z , Wu T , Ma X , et al. A Dynamic Multiobjective Evolutionary Algorithm Based on Decision Variable Classification[J]. IEEE Transactions on Cybernetics, 2020, PP(99):1-14. 的论文学习笔记，只供学习使用，不作商业用途，侵权删除。并且本人学术功底有限如果有思路不正确的地方欢迎批评指正！

Abstract

• 目前许多动态多目标进化算法DMOEAS主要是将多样性引入或预测方法与传统的多目标进化算法相结合来解决动态多目标问题DMOPS。其中种群的多样性和算法的收敛性的平衡十分重要。
• 本文提出了基于决策变量分类的动态多目标优化算法DMOEA-DCV
• DMOEA-DCV将在静态优化阶段将决策变量分成两到三个不同的组，并且在相应阶段分别进行改变。在静态优化阶段，两个不同分组的决策向量使用不同的交叉算子以加速收敛保持多样；在改变反馈阶段，DMOEA-DVC分别采用维护、预测和多样性引进策略重新初始化决策变量组。
• 最后在33个DMOP benchmark上和先进的DMOEA进行了比较，取得了更优异的结果。

Introduction

• DMOPs就是解决随时间变化的多目标优化问题。传统的DMOEA算法强调能够随着环境的改变动态响应，主流的算法可以分为 多样性引进策略diversity introduction approaches[1],[19]-[24]和预测方法 prediction approaches.[25]-[33]

对于diversity introduction approaches的方法：

• 优点： Diversity introduction approaches introduce a certain proportion of randomized or mutated individuals into the evolution population once a change occurs to increase the population diversity. The increase of diversity can facilitate the algorithms to better adapt to the new environment.
• 缺点： However, since these algorithms mainly rely on the static evolution search to find the optimal solution set after diversity introduction, the convergence might be slowed down.

对于Prediction approaches的方法：

• 优点： 在变换的环境中提升收敛性能
• 缺点：预测模型性能受限

目前存在的问题

• 目前的方法不care决策变量之间的差异，使用相同的方式进行考虑，对于平衡种群的多样性和收敛性效率低。

提出基于变量分类的DMOEA(DMOEA-DVC)

• DMOEA-DVC特点在于集合了diversity introduction, fast prediction models和decision variable classification methods, 多样性引入和决策变量分类可以抵消彼此固有的缺陷。
• 静态优化时采用变量分类策略，改变相应阶段时对不同的变量采用不同的进化算子和响应机制。

对比算法

• DNSGA-II-B [1]
• population prediction strategy (PPS) [25]
• MOEA/D-KF [26]
• steady state and generational evolutionary algorithm (SGEA) [33]
• Tr-DMOEA [35]
• DMOEA-CO [52]

benchmark

• five FDA benchmarks [4]
• three dMOP benchmarks [19]
• two DIMP benchmarks [41]
• nine JY benchmarks [42]
• 14 newly developed DF benchmarks [43].

贡献

• 两种决策变量分类方法
• 静态优化时，对两种变量采用不同的进化方式
• change responce时，使用保持，预测和引入多样性混合响应策略以应对三种不同的决策变量。

BACKGROUND AND RELATED WORK

Basics of DMOP

动态帕累托最优解和动态帕累托最优解集

• 基本上就是加上了时序t的概念的支配
  

多最优变量与单最优变量

• 注意这里的exist和any的表述！！
  
• 换言之，如果一个决策变量是单最优变量，那么PS()(t)上的这个变量具有相同的值，而如果这个决策变量是多最优变量，那么PS(t)上的这个变量具有不同的值

DMOP问题的类型

DMOEA

• DMOEA基本上可以分为两类：引入多样性diversity introduction 和 基于预测predictionbased approaches.

diversity introduction

• diversity introduction 考虑的是当环境改变发生时，引入随机的或变异的个体来避免种群多样性的损失。
• Deb[1] DMOEAs : proposed two DMOEAs (DNSGAII- A and DNSGA-II-B) based on NSGA-II [7]. Once a change is detected, DNSGA-II-A randomly reinitializes 20% of the individuals, while DNSGA-II-B randomly mutates 20% of the individuals.
• Goh and Tan [19] dCOEA: introduced a competitive-cooperative coevolutionary algorithm (dCOEA) where some new individuals are generated randomly to enhance the diversity of the population when the environment changes.
• Helbig and Engelbrecht [20] HDVEPSO: proposed a heterogeneous dynamic vector-evaluated particle (非均匀动态矢量评估粒子) swarm optimization (HDVEPSO) algorithm by combining heterogeneous particle swarm optimization (HPSO) [21], [22] and dynamic vector-evaluated particle swarm optimization (DVEPSO) [23]. HDVEPSO randomly reinitializes 30% of the swarm particles after the objective function changes.
• Martínez-Peñaloza and Mezura-Montes [24] combined generalized differential evolution (DE) along with an artificial immune system to solve DMOP (Immune-GDE3).
• 总结，使种群不易陷入局部最优并且易于实现。

predictionbased approaches

• 为了使种群易于适应变换后的新的环境，提出了预测的方法
• Zhou et al. [25] presented a PPS to divide the population into a center point and a manifold 中心和支管. The proposed method uses an autoregression (AR) 自回归 model to locate the next center point and uses the previous two consecutive manifolds 连续不断的支管 to predict the next manifold. The predicted center point and manifold make up a new population more suitable to the new environment.
• Muruganantham et al. [26] applied a Kalman filter [44] 卡尔曼滤波器 in the decision space to predict the new Pareto-optimal set. They also proposed a scoring scheme to decide the predicting proportion. 评分机制
• Hatzakis and Wallace [27] 自回归和边界点
• Peng [28] 改进 exploration 和 exploitation 算子
• Wei and Wang [29] hyperrectangle prediction (超矩形预测)
• Ruan [30] gradual search (逐步搜索)
• Wu et al. [31] reinitialized individuals in the orthogonal direction (正交方向) to the predicted direction of the population in change response.
• Ma et al. [32] utilized a simple linear model to generate the population in the new environment.
• Jiang and Yang [33] introduced an SGEA, which guides the search of the solutions by a moving direction from the centroid of the nondominated solution set to `the centroid of the entire population. The step size of the search is defined as the Euclidean distance between the centroids of the nondominated solution set at time steps (t−1) and t.
• 总结：预测的方法提高了算法的收敛效率
• 本文通过结合多样性引入和基于快速预测的方法来利用两者的优点，提出了一种增强的变化响应策略。

Decision Variable Classification Methods

• 无论是多样性引入还是预测方法都可以被视为在搜索最优解时的概率模型。大多数现有的DMOEA都假定所有决策变量都在相同的概率分布下。 但是，在实际的DMOP中，决策变量的概率分布可能会发生很大变化。 通过决策变量分类，可以将决策变量分为不同的组，然后可以将特定的概率搜索模型应用于相应的变量组以获得更好的解决方案。

基于扰动的变量分类

在静态问题中

• 例如，在[45]-[48]中通过决策变量扰动实现了决策变量分类。 决策变量扰动会产生大量个体进行分类，并成比例地消耗大量适应性评估。 该策略对于静态MOP效果很好，在静态MOP中，决策变量的类别不变，并且仅需要分类一次。

在动态问题中

• 决策变量的分类经常变化，因此需要更多次数的分类和评价次数
• 很少有方法将决策变量分类的方法运用到动态问题中，现有的静态问题的方法不太合适。
• Woldesenbet和Yen [51]通过对目标空间变化的平均敏感度来区分决策变量，并以此为基础来重新安置个体。 该方法对于动态单目标优化问题效果很好，但是不适用于DMOP。
• Xu[52]提出了一种针对DMOP的协作式协同进化算法，其中决策变量被分解为两个子组件，即相对于环境变量t不可分离和可分离的变量。 应用两个种群分别协同优化两个子组件。 文献[52]中提出的算法在基于环境敏感性可分解决策变量的DMOP上具有优越性，但是，在许多DMOP中可能并非如此。

本文提出的方法

• 在本文中，我们提出了一种适用于大多数DMOP的更通用的决策变量分类方法。所提出的方法没有使用额外的目标评估或迭代积累来收集统计信息就实现了准确的分类。特别地，决策变量分类方法使用决策变量和目标函数之间的统计信息，该统计信息在每次环境变化之后的第一次迭代中可用，也就是说，不需要消耗额外的适应性评估。值得强调的是，本文提出的分类是区分DMOP中决策变量分布（即单个最优值或多个最优最优值）的首次尝试。从搜索开始，就采用了不同的策略来采样不同的决策变量。这样，决策变量可以在迭代过程中尽可能服从PS（t）的分布，从而更好地覆盖和逼近PS（t）。

提出的框架和实现

变量分类Decision Variable Classification

• 文中提出的变量分类分为两种，一种对应算法1 line 6 ,静态优化时的变量分类，一种对应算法1 line9 ,动态优化时的变量分类。

Decision Variable Classification in Static Optimization

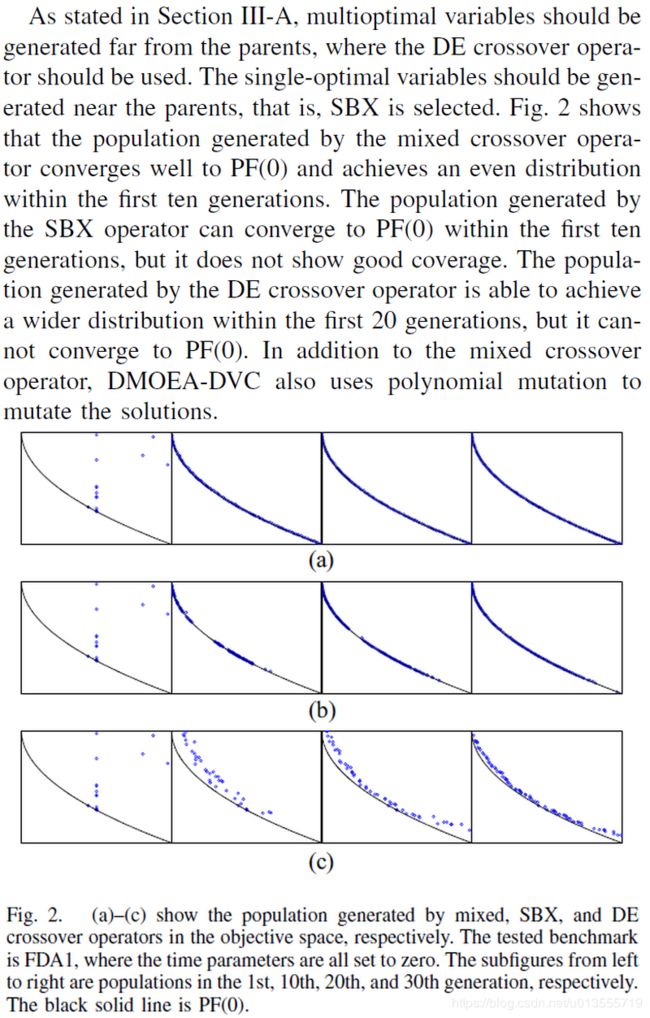
首先变量可以被分为single optimal收敛 和multi-optimal多样

• 一句话概括一下：对于single optimal的维度应该和最好的个体越近越好，而multi-optimal的维度则应当越远越好。否则易陷入局部最优，并且在迭代早期精英策略会导致multi-optimal的维度也向最优解靠拢，影响多样性。

区分single optimal收敛 和multi-optimal变量

• 如果目标函数在一个变量上矛盾,则这个变量是multi-optimal的
• In DMOP, the objective functions could conflict with each other on some decision variables [46], [53]. If two objective functions conflict on a decision variable, the decision variable is deemed to have multiple optimal values.

具体操作：

(自我思考)这里需要考虑一个问题，就是当一个变量进行改变时，其他变量也不是相同的，如何去单独考虑一个变量对于整体的变化，如果变量的维度大，如何证明是这个变量而不是其他变量的变化导致目标函数的变化呢？这里解释是在DOMP中，一般只有一个变量是multi的，而其余都是single的，这个解释觉得还可以进一步完善和改进。但是作为节省计算资源而言，这的确是一个比较折中的办法

使用SRCC来评价变量和目标函数之间的关系

大体思想是，将种群中所有个体的这个变量从低到高进行排序，然后对种群中这些个体的单个目标值进行进行排序，这两个排序的rank差值就是这个个体的d(i,j,k).然后通过d(i,j,k)来计算r,而当r大于或者小于一个阈值的时候，就意味着变量i和目标j具有正相关或者负相关性

算法流程

Decision Variable Classification in Change Response

• 在DMOP中，决策变量可分为similar ,predictable 和 unpredictable
  • similar 变量：在连续两次环境变化中没有什么变化，环境变化时，不需要重新初始化
  • predictable 变量： 在环境变化中，预测可以带来显著提升，环境变化时，需要通过预测的方式重新初始化
  • unpredictable 变量：预测几乎带来不了提升，环境变化时，通过引入多样性重新初始化
• 非参数的t检验被用于评价决策变量改变和环境的相关性 ，对于当前第i个变量与上个世代的第i个变量之间的关系可以表示为：
  

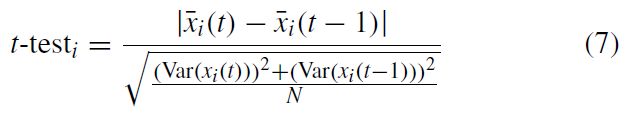
使用t检验区分变量-相似性与非相似性变量

对于非相似性变量，判断其是否是可以预测的变量

• x_center表示种群中所有个体的决策变量的平均值，x_trial[i]表示种群中x_center第i个决策变量经过预测的方法变化后的结果而其余的变量保持不变，如果x_trial[i]能够支配x_center则表示这个第i个决策变量是可以预测的，否则则认为第i个决策变量是不能预测的。

对于某些问题，预测的方法不可行

算法流程

环境选择

• DMOEA-DVC和SGEA[33]使用相同的选择方法，适应度函数F(i)表示支配个体xi的个体数目
• 如果存档A中个体少于N则从种群中挑选最好的个体进P’，如果刚好相等，就将A中所有个体转入P’，如果存档A中个体多了就从种群中挑选最远的个体进P’.

改变响应

• 对于环境改变后的响应，对于DMOEA-DVC中分类出的三种变量，分别使用maintenance保持,diversity introduction 多样性引入和prediction approach 预测方式三种对决策变量进行处理。

maintenance 保持

• 如果变量是相似的则保持不变

Diversity Introduction

• 如果变量不可预测
  

使用kalman进行预测

• 如果对预测方式不清楚可以参考[25]和[33]
• 如果变量可以预测
  
  

生成子代

• 论文认为SBX生成的子代会离父代很近，因此适合single-optimal的决策变量，而DE生成的子代里父代很远，因此适合multi-optimal的决策变量
  
  
• 总体流程
  

个体更新规则

• 详见[33]
  

计算复杂度

[1] K. Deb, U. V. Rao, and S. Karthik, “Dynamic multi-objective optimization and decision-making using modified NSGA-II: A case study on hydro-thermal power scheduling,” in Proc. EMO, vol. 4403, 2007, pp. 803–817.
[4] M. Farina, K. Deb, and P. Amato, “Dynamic multi-objective optimization problems: Test cases, approximations, and applications,” IEEE Trans. Evol. Comput., vol. 8, no. 5, pp. 425–442, Oct. 2004.
[19] C.-K. Goh and K. C. Tan, “A competitive-cooperative coevolutionary paradigm for dynamic multi-objective optimization,” IEEE Trans. Evol. Comput., vol. 13, no. 1, pp. 103–127, Feb. 2009.
[20] M. Helbig and A. P. Engelbrecht, “Heterogeneous dynamic vector evaluated particle swarm optimization for dynamic multi-objective optimization,” in Proc. IEEE Congr. Evol. Comput. (CEC), 2014, pp. 3151–3159.
[21] A. P. Engelbrecht, “Heterogeneous particle swarm optimization,” in Proc. Int. Conf. Swarm Intell., 2010, pp. 191–202.
[22] M. A. M. de Oca, J. Peña, T. Stützle, C. Pinciroli, and M. Dorigo, “Heterogeneous particle swarm optimizers,” in Proc. IEEE Congr. Evol. Comput. (CEC), 2009, pp. 698–705.
[23] M. Greeff and A. P. Engelbrecht, “Solving dynamic multi-objective problems with vector evaluated particle swarm optimization,” in Proc. IEEE Congr. Evol. Comput. (CEC), 2008, pp. 2917–2924.
[24] M. Martínez-Peñaloza and E. Mezura-Montes, “Immune generalized differential evolution for dynamic multi-objective optimization problems,” in Proc. IEEE Congr. Evol. Comput. (CEC), 2015, pp. 846–851.
[25] A. Zhou, Y. Jin, and Q. Zhang, “A population prediction strategy for evolutionary dynamic multi-objective optimization,” IEEE Trans. Cybern., vol. 44, no. 1, pp. 40–53, Jan. 2014.
[26] A. Muruganantham, K. C. Tan, and P. Vadakkepat, “Evolutionary dynamic multi-objective optimization via Kalman filter prediction,” IEEE Trans. Cybern., vol. 46, no. 12, pp. 2862–2873, Dec. 2016.
[27] I. Hatzakis and D. Wallace, “Dynamic multi-objective optimization with evolutionary algorithms: A forward-looking approach,” in Proc. ACM Conf. Genet. Evol. Comput., 2006, pp. 1201–1208.
[28] Z. Peng, J. Zheng, J. Zou, and M. Liu, “Novel prediction and memory strategies for dynamic multi-objective optimization,” Soft Comput., vol. 19, no. 9, pp. 2633–2653, 2014.
[29] J. Wei and Y. Wang, “Hyper rectangle search based particle swarm algorithm for dynamic constrained multi-objective optimization problems,” in Proc. IEEE Congr. Evol. Comput. (CEC), 2012, pp. 259–266.
[30] G. Ruan, G. Yu, J. Zheng, J. Zou, and S. Yang, “The effect of diversity maintenance on prediction in dynamic multiobjective optimization,” Appl. Soft Comput., vol. 58, pp. 631–647, Sep. 2017.
[31] Y. Wu, Y. Jin, and X. Liu, “A directed search strategy for evolutionary dynamic multi-objective optimization,” Soft Comput., vol. 19, no. 11, pp. 3221–3235, 2015.
[32] Y. Ma, R. Liu, and R. Shang, “A hybrid dynamic multi-objective immune optimization algorithm using prediction strategy and improved differential evolution crossover operator,” in Proc. Neural Inf. Process., vol. 7063, 2011, pp. 435–444.
[33] S. Jiang and S. Yang, “A steady-state and generational evolutionary algorithm for dynamic multi-objective optimization,” IEEE Trans. Evol. Comput., vol. 21, no. 1, pp. 65–82, Feb. 2017.
[35] M. Jiang, Z. Huang, L. Qiu, W. Huang, and G. G. Yen, “Transfer learning based dynamic multiobjective optimization algorithms,” IEEE Trans. Evol. Comput., vol. 22, no. 4, pp. 501–514, Aug. 2018, doi: 10.1109/TEVC.2017.2771451.
[41] W. Koo, C. Goh, and K. C. Tan, “A predictive gradient strategy for multi-objective evolutionary algorithms in a fast changing environment,” Memetic Comput., vol. 2, no. 2, pp. 87–110, 2010.
[42] S. Jiang and S. Yang, “Evolutionary dynamic multi-objective optimization: Benchmarks and algorithm comparisons,” IEEE Trans. Cybern., vol. 47, no. 1, pp. 198–211, Jan. 2017.
[43] S. Jiang, S. Yang, X. Yao, and K. C. Tan, “Benchmark functions for the CEC’2018 competition on dynamic multiobjective optimization,” Centre Comput. Intell., Newcastle Univ., Newcastle upon Tyne, U.K., Rep. TRCEC2018, 2018.
[44] A. Muruganantham, Y. Zhao, S. B. Gee, X. Qiu, and K. C. Tan, “Dynamic multi-objective optimization using evolutionary algorithm with Kalman filter,” Proc Comput. Sci., vol. 24, pp. 66–75, Nov. 2013.
[45] X. Zhang, Y. Tian, R. Cheng, and Y. Jin, “A decision variable clustering-based evolutionary algorithm for large-scale many-objective optimization,” IEEE Trans. Evol. Comput., vol. 22, no. 1, pp. 97–112, Feb. 2018.
[46] X. Ma et al., “A multiobjective evolutionary algorithm based on decision variable analysis for multiobjective optimization problems with largescale variables,” IEEE Trans. Evol. Comput., vol. 20, no. 2, pp. 275–298, Apr. 2016.
[47] C. K. Goh, K. C. Tan, D. S. Liu, and S. C. Chiam, “A competitive and cooperative co-evolutionary approach to multi-objective particle swarm optimization algorithm design,” Eur. J. Oper. Res., vol. 202, no. 1, pp. 42–54, 2010.
[48] M. N. Omidvar, X. Li, Y. Mei, and X. Yao, “Cooperative co-evolution with differential grouping for large scale optimization,” IEEE Trans. Evol. Comput., vol. 18, no. 3, pp. 378–393, Jun. 2014.
[49] J. Sun and H. Dong, “Cooperative co-evolution with correlation identification grouping for large scale function optimization,” in Proc. Int. Conf. Inf. Sci. Technol. (ICIST), 2013, pp. 889–893.
[50] M. N. Omidvar, X. Li, and X. Yao, “Cooperative co-evolution with delta grouping for large scale non-separable function optimization” in Proc. IEEE Congr. Evol. Comput., 2010, pp. 1762–1769.
[51] Y. G. Woldesenbet and G. G. Yen, “Dynamic evolutionary algorithm with variable relocation,” IEEE Trans. Evol. Comput., vol. 13, no. 3, pp. 500–513, Jun. 2009.
[52] B. Xu, Y. Zhang, D. Gong, Y. Guo, and M. Rong, “Environment sensitivity-based cooperative co-evolutionary algorithms for dynamic multi-objective optimization,” IEEE/ACM Trans. Comput. Biol. Bioinform., vol. 15, no. 6, pp. 1877–1890, Nov./Dec. 2017.
[53] S. Huband, P. Hingston, L. Barone, and L. While, “A review of multiobjective test problems and a scalable test problem toolkit,” IEEE Trans. Evol. Comput., vol. 10, no. 5, pp. 477–506, Oct. 2006.
[54] B. Student, “The probable error of a mean,” Biometrika, vol. 6, no. 1, pp. 1–25, 1908.
[55] D. Wang, H. Zhang, R. Liu, W. Lv, and D. Wang, “t-test feature selection approach based on term frequency for text categorization,” Pattern Recognit. Lett., vol. 45, no. 1, pp. 1–10, 2014.
[56] B. Chen, W. Zeng, Y. Lin, and D. Zhang, “A new local search based multi-objective optimization algorithm,” IEEE Trans. Evol. Comput., vol. 19, no. 1, pp. 50–73, Feb. 2015.
[57] C. Chen and L. Y. Tseng, “An improved version of the multiple trajectory search for real value multi-objective optimization problems,” Eng. Optim., vol. 46, no. 10, pp. 1430–1445, 2014.
[58] C. Rossi, M. Abderrahim, and J. C. Díaz, “Tracking moving optima using Kalman-based predictions,” Evol. Comput., vol. 16, no. 1, pp. 1–30, 2008.