【算法-枚举】熄灯问题 通俗详细的解题叙述（OpenJudege-2811）

算法–熄灯问题

对于该问题的描述：

https://www.bilibili.com/video/av10046345/?p=4 #p4熄灯问题
http://bailian.openjudge.cn/practice/2811/ #OpenJudege-2811

本题解法：枚举

解法来源:https://www.bilibili.com/video/av10046345/?p=4 #p4熄灯问题

上链视频中已经讲解得已经非常好，非常清晰，但是对于水平不高的人来说，其中仍有一部分内容不太友好。
我将对上链本问题的解法进行更详细的阐述,我会尽量让其中的难点显得直观一些，希望能够帮到你！

首先，本问题的解题思想大致为：

1.如果对整个press矩阵（即为解）进行枚举，将会有2^30可能，这是不可行的

2.经过观察，可以发现如果要关闭某行打开的灯，可以在下一行的对应位置按下开关（下图为两个例子，不能代表所有情况，但你可以暂时这么直观地理解）

红色为按钮按下位置，红色加黄色区域即为该按钮的作用范围。


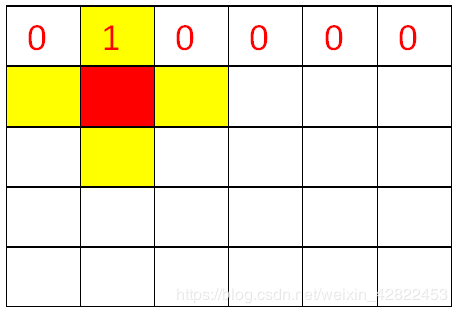
3.如果使用上面的方法，我们可以发现：
（1）、当第一行的开关确定以后，经过这些开关作用，第一行的亮灯状态也确定了下来，第二行需要在什么地方按下开关就已经固定了（为了熄灭第一行所有的灯）
Ps：这里的第一行开关并没有要求去关闭任何灯，只是将第一行灯的状态确定了下来，同时为了关闭第一行灯，我们第二行开关的状态也随之确定了下来

（2）、在第二行按下了开关，将第一行灯全部关闭的同时，也对第二行灯的状态产生了作用，此时第二行的灯的状态也确定了。那么在第三行要按下哪些开关也就固定了下来（为了熄灭第二行的灯）
（3）、以此类推，一直到最后两行时，为了熄灭倒数第二行的灯，最后一行要按的开关也固定了下来
（4）、但是要熄灭最后一行的灯，我们并没有再往下一行的开关供我们做上述的操作了。

（5）、由此，我们就必须找到一种搭配，使得最后一行开关对第倒数第二行灯进行熄灭的同时，也将最后一行灯全部熄灭了
（6）、由于当第一行开关确定下来的同时，后面的所有开关也都依次固定了下来（为了熄灭前一行的灯），我们只需要改变第一行开关，就可以对剩余行的开关进行改变
（7）、那么我们可以对第一行开关所有的可能性进行枚举，来找出可以使得所有灯熄灭的开关组合，对第一行开关进行枚举的操作数为2^6，共64种可能，这是合理可行的

代码实现：

灯存放：二位数组 puzzle
开关/解存放：二维数组 press
同时，为了简化我们的操作，我们可以使用6*8的数组来存放灯和开关，这样在特别的边/角位置我们就可以不用使用特定的操作，整个数组各个区域都使用同一种操作即可（如果没有这样类似于缓冲区的部分，那么就可能会造成index超出）
所以：
灯存放：puzzle[6][8]
开关/解存放: press[6][8]

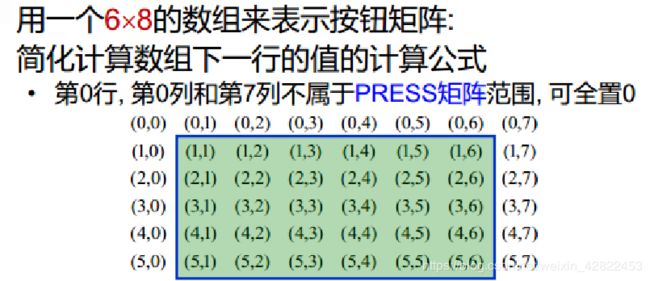
主要的函数及功能：

1.生成第一行开关的所有可能: enumerate()

2.每次取第一行开关的一种可能，生成剩余的开关行，并且检查这种组合是否能熄灭所有的灯: guess()

代码（没有详细核对注释，请选择性参考）：

#include 
#define False 0
#define True 1
typedef int bool;

int press[6][8], puzzle[6][8];

void main()
{
	int row, column, cases, c;//cases 为要解决的案例个数
	void enumerate(void);
	//此处获取循环次数
	printf("请输入案例个数：");
	scanf("%d", &cases);
	for (c = 1; c <= cases; c++)//根据案例数循环多次，获取puzzle输入--生成可能并判断--输出打印
	{
		printf("\n请输入第%d个矩阵：\n", c);
		for (row = 1; row < 6; row++)
			for (column = 1; column < 7; column++)//获取输入，scanf会自动忽略回车，所以可以一行一行输入，注意加 ， 号
			{
				scanf("%d,", &puzzle[row][column]);
			}//此时puzzle已经赋值完毕

		enumerate();//对press，puzzle处理，最终press匹配正确才结束执行


		printf("\n#################\nPuzzle%d\n", c);
		//press此时已经为正确状态，下面进行打印输出
		for (row = 1; row < 6; row++) {
			for (column = 1; column < 7; column++) {
				printf("%d ", press[row][column]);
			}
			printf("\n");//每行一个回车分隔
		}
	}
	getchar();
}


void enumerate()
{	//枚举开关数组第一行64种组合（其实加上第一行开关全为0的情况，共65种可能
	int guess(void);
	int row, column;

	for (row = 0; row < 6; row++) {//将press每行第一个，和最后一个元素置0（即多出来的部分
		press[row][0] = 0;
		press[row][7] = 0;
	}

	for (column = 1; column < 7; column++)//将最顶上一行置0
	{
		press[0][column] = 0;
	}

	for (column = 1; column < 7; column++)//将press有效行第一行填0， 同时这也是第一种搭配
	{
		press[1][column] = 0;
	}

	while (guess() == 0)//给第一行赋值以后，使用guess生成剩下的部分并且判断第一行是否是正确状态
	{
		//如果guess返回0，则第一行不正确，对其加1求下一种可能
		press[1][1]++;
		column = 1;
		while (press[1][column] > 1)
		{
			press[1][column] = 0;
			column++;
			press[1][column]++;
		}
	}
	//直到press有了正确的组合，enumerate才完成执行
}


int guess(void)
{
	int row, column;

	for (row = 1; row < 5; row++)//循环,根据第一行把press填满
		for (column = 1; column <= 6; column++)
		{
			press[row + 1][column] = (press[row][column - 1] + press[row][column] + press[row][column + 1] + press[row - 1][column] + puzzle[row][column]) % 2;
		}

	for (column = 1; column < 7; column++)//检查最后一行是否全部熄灭
	{
		if ((press[5][column - 1] + press[5][column] + press[5][column + 1] + press[4][column]) % 2 != puzzle[5][column])//如果目标灯附近的按钮作用后最终结果与灯状态不相等，则灯会被点亮，会错误匹配返回0
		{
			return 0;
		}
	}

	return 1;//如果没有在for循环中返回，则最后一行灯全部熄灭，检查通过，返回1
}

代码中的难点：

1.对第一行开关的64种可能进行枚举的方法：
这段代码具体为：

while (guess() == 0)//给第一行赋值以后，使用guess生成剩下的部分并且判断第一行是否是正确状态
	{
		//如果guess返回0，则第一行不正确，对其加1求下一种可能
		press[1][1]++;
		column = 1;
		while (press[1][column] > 1)
		{
			press[1][column] = 0;
			column++;
			press[1][column]++;
		}
	}

这段代码中的的功能该图已经做了阐述，但是我想我可以更详细的的说明一下：

这种枚举的方法，将整个开关数组的第一行看做一整个6位2进制数（6位二进制数正好可以表示64个不同的值）

我们从 0 0 0 0 0 0 开始，每次给这个二进制数加1， 就可以得到64个不同的值（同时对应的也就是64种不同的开关状态）

但是我们这里实际上是多维数组的一整行元素，其中的值（0 或 1）也都是十进制数，对于前面提到的对这个“二进制数”每次加1的操作，

要通过我们手动来实现，主要代码就是这一段：

		//开关第一行此时已经全部被赋值为0
		press[1][1]++;//给第一行第一个元素加1
		column = 1;
		while (press[1][column] > 1)//如果这个位置的值已经大于1了（即为2），此处默认从第一行第一列开始判断
		{
			press[1][column] = 0;//就将这个位置的值置为0
			column++;//移位到后一位
			press[1][column]++;//给后一位的数字加1，并且返回到while部分去判断该位置加1后是否大于1，如果大于1，又进来做同样的操作----将该位置置为0，往后一个位置加
		}
//这样的一整个过程，就对第一行的这个“二进制数”完成了加1的操作，即生成了一种新的开关组合

生成的结果，大概会是这样（注意，这里面每个数字其实是分别存在数组的同一行的）：

如果你不习惯，其实还可以将顺序反回来，让生成的结果成为这样：

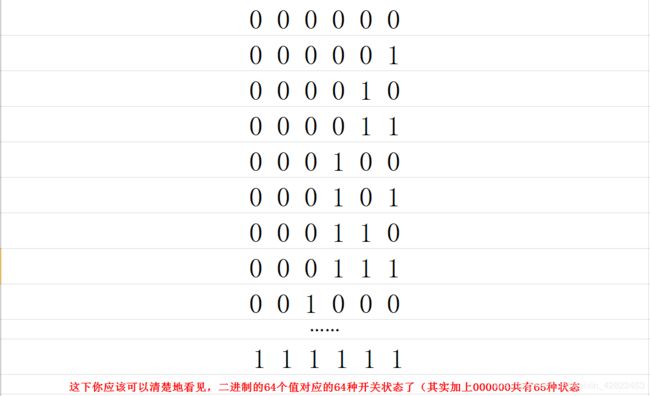
只需要将代码微微修改

		press[1][6]++;//从最右边的一个元素加1
		column = 6;//从最右边开始位移
		while (press[1][column] > 1)
		{
			press[1][column] = 0;
			column--;//位移方向相反，为从右向左位移
			press[1][column]++;
		}

我将这些贴出来，是希望让你理解，这段代码到底枚举生成了什么，是怎么生成的

我希望你可以理解这部分，如果还不行，你自己用笔在纸上模拟一遍，很快就会弄明白。

2.具体地判断某个开关是否需要被按下：
这一段的代码为：

		for (row = 1; row < 5; row++)//循环,根据第一行把press填满
		for (column = 1; column <= 6; column++)
		{
			press[row + 1][column] = (press[row][column - 1] + press[row][column] + press[row][column + 1] + press[row - 1][column] + puzzle[row][column]) % 2; //这一段代码为要理解的目标
		}

我们假设上述代码运行到了row = 1, column = 2的位置，我们用图来看看发生了什么：

这里我用：

0代表“缓冲部分”

与此相对的，红色和绿色部分分别代表puzzle，press的正真有效部分

黑色方块就是我们这次要确定的开关：即为 press[row + 1][column]

而黄色方块，分别对应press[row][column - 1] ， press[row][column] ， press[row][column + 1] ，
press[row - 1][column] ，puzzle[row][column]

实际上，根据我们之前的逻辑，黑色方块处的开关是否操作，由puzzle中黄色方块处的灯的状态决定（如果该灯是开着的，黑色开关则需要操作，如果该灯是关闭的，则黑色开关不操作）
那么，怎么才能知道该灯现在的状态呢？

我们找出了所有会对该灯产生作用的，已经按下过的开关（即press中的黄色方块），将这些开关累加，若结果是偶数，代表这些开关起的作用相互抵消了，若是奇数，代表最终对puzzle中的黄块位置的灯改变了一次状态。由于该灯自身也有状态，我们可以将该灯的状态在前面一起累加，然后将结果对2取模来确定该灯经过这些开关作用后的最终状态（偶数为灯灭，取模得到0，奇数为灯亮，取模为1）

这里最优雅的部分就在：在没有改变puzzle灯原有状态的情况下，得到了puzzle中灯被press中相应开关操作过后的结果，并且根据这个结果继续生成press剩余的开关值

希望你能理解。如果还是不行，一样的，我推荐你画个图试一试

3.如何判断最后一行灯是否全部熄灭了
代码：

for (column = 1; column < 7; column++)//检查最后一行是否全部熄灭
	{
		if ((press[5][column - 1] + press[5][column] + press[5][column + 1] + press[4][column]) % 2 != puzzle[5][column])//如果目标灯附近的按钮作用后最终结果与灯状态不相等，则灯会被点亮，会错误匹配返回0

这里与前述的判断某个开关是否需要被按下使用了类似的方法，只是稍有不同

这里以检查puzzle中黑色块位置的灯是否被关闭为例，右侧press的黄色开关，为可以对该灯产生作用的开关。

这里的代码将这些开关的值累加起来，对他们取模，判断最后是否对该灯进行了操作（与前相同，累加的和为偶数，则各个开关的作用相互抵消了，如果为奇数，则最终最该灯进行了一次状态改变）

这里与前不同的是：这里没有将灯的原始状态拿去累加，而是检查多个开关作用后的最终结果与灯的原始状态是否相等，相等则该灯关闭

怎么理解呢？
多个开关作用后会有两个最终结果
对灯操作一次：1
开关作用抵消：0

要判断是否熄灭的灯也有两种状态
原来灯开着：1
原来灯是熄灭的：0

共有4种搭配：
1.开关最终进行一次操作，灯原来是亮着的（即 1 : 1）操作过后，灯是灭的
2.开关最终进行一次操作，灯原来是灭的（即1 : 0）操作过后，灯是亮的
3.开关最终相互抵消，灯原来是亮的（即0 : 1）最终灯是亮的
4.开关最终相互抵消，灯原来是灭的（即0 : 0）最终灯是灭的

可以看出，只有1,4两种情况最终可以得到熄灭的灯，这两种情况，开关最终的作用结果都等于灯的原始状态

这也是为什么检查多个开关作用后的最终结果与灯的原始状态是否相等，相等则该灯关闭

上述就是全部了，你可以选择性食用，希望能帮到你。

如有错误，还望指出，感激不尽！