数据结构与算法python版【慕课听课笔记】

一、算法分析

1、大O表示法

1.1 算法时间度量指标

将一个算法实施的操作步骤数作为独立于具体程序/机器的度量指标。
在算法分析中一般将赋值语句作为算法步骤的度量。因为一条赋值语句中包含了计算（表达式）和存储（变量）两个程序设计中的基本内容。

1.2 数量级函数

根据赋值语句计算得到基本操作数量函数$T(n)$，用数量级函数$O(f(n))$描述$T(n)$中随问题规模$n$增加而变化速度最快的主导部分。
一般当问题规模较小时难以确定数量级之间的差异。

2、python数据类型的影响

2.1 list和dict操作对比

• 索引：list通过自然数进行索引list[i]，dict通过键名进行索引dict[key]
• 添加：list通过append(), extend(), insert()方法进行添加，dict通过语句ditc[key] = value直接添加
• 删除：list通过pop(), remove()方法进行删除，dict通过del语句进行删除:del dic[key]
• 更新：list:a[i] = v，dict:b[k] = v

2.2 List类型常用操作性能

• 按索引取值和赋值（v = a[i], a[i] = v)，由于列表的随机访问特性，这两个操作执行时间与列表大小无关
• 列表增长：list.append()方法，执行时间$O(1)$；加法操作符：lst = lst + [v]，执行时间$O(n+k)$
  通过编写代码来实际比较一下运行时间：

## 加法运算符添加列表
def test1():
	l = []
	for i in range(1000):
		l = l + [i]

## append方法添加列表
def test2():
	l = []
	for i in range(1000):
		l.append(i)

## 使用列表解析的方法生成数值型列表
## 将for循环和创建新元素的代码合并成一行
## 第一个式子是表达式，可以换成其他形式：l = [i ** 2 in range(100)]
def test3():
	l = [i for i in range(1000)]

## 使用函数list()将range()的结果直接转换为列表
## 实际上使用range()函数时还可以指定步长：range(2,11,2)
def test4():
	l = list(range(1000))


from timeit import Timer
## Timer(stmt = '', setup = '', time.time = )
## 第一个参数表示要测试的代码语句，第二个参数表示执行代码的准备工作
## Timer.timeit(number = )返回执行代码的平均耗时，类型为float
t1 = Timer("test1()", "from __main__ import test1")

## print语句的格式化输出，与C语言相似
## %字符表示转换说明符的开始
## 如果有多个转换说明符，后面用括号隔开
print("concat %f seconds\n" %t1.timeit(number = 1000))

t2 = Timer("test2()", "from __main__ import test2")
print("append %f senconds\n" %t2.timeit(number = 1000))

t3 = Timer("test3()", "from __main__ import test3")
print("comprehension %f senconds\n" %t3.timeit(number = 1000))

t4 = Timer("test4()", "from __main__ import test4")
print("list range %f senconds\n" %t4.timeit(number = 1000))

通过比较可以发现方法4最快，方法3（解析法）次之，加法运算符最慢
下图表示了List基本操作的数量级：

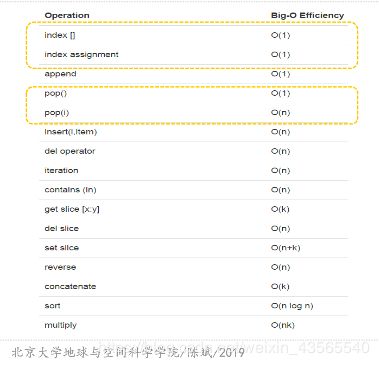
我们注意到在这里pop(i)的复杂度为$O(n)$这是因为Python在中部移除元素后，需要把后面的元素全部向前挪一位，这种实现方法虽然降低了pop(i)操作的速度，但是提高了列表按索引取值和赋值的操作速度。
用代码来观察一下pop()和pop(0)实现速度上的差别：

import timeit
popzero = timeit.Timer("x.pop(0)", "from __main__ import x")
popend = timeit.Timer("x.pop()", "from __main__ import x")
print("pop(0) pop()")
for i in range(1000000, 100000001, 1000000):
	x = list(range(i))
	pt = popend.timeit(number = 1000)
	x = list(range(i))
	pz = popzero.timeit(number = 1000)
	print("%15.5f, %15.5f" %(pz,pt))

2.3 列表和字典操作性能

列表和字典中都有操作符in，来比较一下哪个查找得更快：

import timeit
import random

num = 10000

t = timeit.Timer("random.randrange(%d) in x"%num,
				"from __main__ import random,x")

x = list(range(num))
lst_time = t.timeit(number = 1000)

x = {j: None for j in range(num)}
d_time = t.timeit(number = 1000)

print("%d,%10.3f, %10.3f" %(num, lst_time, d_time))

2.4 习题

习题1：编程程序，验证List的按索引取值是$O(1)$的

import timeit
import random

for i in range(100, 1000, 10):
	t = timeit.Timer("x[random.randrange(%d)]"%i, "from __main__ import random,x")
	x = list(range(i))
	print("time is %f" %t.timeit(number = 1000))

习题2：编写程序，验证dict的get item和set item操作都是$O(1)$的

import timeit
import random

for i in range(100, 1000, 10):
	t1 = timeit.Timer("x[random.randrange(%d)]"%i, 
				"from __main__ import random,x")
	x = {j : None for j in range(i)}
	

	t2 = timeit.Timer("x[random.randrange(%d)] = 0" %i, 
					"from __main__ import random,x")
	print("get item's time is %f, set item's time is %f" 
		%(t1.timeit(number = 1000), t2.timeit(number = 1000)))

习题3：编写程序，比较list和dict的del操作符性能

import timeit
import random

for i in range(100, 1000, 10):
	t1 = timeit.Timer("del x[10]", "from __main__ import x")
	x = list(range(i))
	lst_time = t1.timeit(number = 1000)

	t2 = timeit.Timer("del x[10]", 
					"from __main__ import x")
	x = {j : None for j in range(i)}
	dict_time = t2.timeit(number = 1000)
	
	print("list's del time is %f, dic's del time is %f" 
		%(lst_time, dict_time))

习题4：编写程序，验证list.sort()的时间复杂度为$O(nlogn)$：

import timeit
import random

for i in range(1000, 10000, 100):
	t = timeit.Timer("x.sort()", "from __main__ import x")
	x = [random.randrange(10**6) for n in range(5*i)]

	print("time is %f" %t.timeit(number = 1000))

OJ适应性测试：
习题5：给定若干个整数，找出这些整数中最小的，输出。

str_in = input("输入多个数字，用空格分隔")

num = [int(n) for n in str_in.split()] ##注意这种创建列表的方法
m = num[0]

for i in range(1,len(num)):
	if num[i] > m:
		m = num[i]

print(m)

二、基本结构

2.1 线性结构

线性结构时一种有序数据项的集合，其中每个数据项都有唯一的前驱和后驱

• 只有第一项没有前驱，最后一项没有后驱
• 新的数据项加入到数据集中时，只会加入到原有的某个数据项之前或之后

不同线性结构的关键区别在于数据项的增减方式。
根据这个特点可以将线性结构分成栈(stack)、队列(queue)、双端队列(deque)和列表(list)

2.2 栈(stack)

2.2.1 栈的定义

栈是一种线性结构，栈中数据项的加入和移除都只发生在线性结构的同一端。
栈的一个特点为后进先出，即距离栈底越近的数据项，留在栈中的时间越长。

2.2.2 用Python实现栈

一般来说栈应该有如下操作：

用列表数据类型来实现栈：

## 用Python实现ADT Stack
class stack():
	def __init__(self):
		self.items = []

	def isEmpty(self):
		return self.items == []

	def push(self, item):
		self.items.append(item)

	def pop(self, item):
		return self.items.pop()

	def peek(self):
		return self.items[-1]

	def size(self):
		return len(self.items)

注意：一般选用列表的最后一个位置作为栈顶，这样push/pop方法的复杂度较低，均为$O(1)$

2.2.3 栈的应用：简单括号匹配

检验思路：对于所有的文本，检验是否为左括号，如果是的话压入栈，然后对于遇到的第一个右括号，将它与栈顶的左括号匹配，并且取出。

def strCheck(symbolString):
	s = stack()
	check = True
	index = 0
	while index < len(symbolString) and check:
		symbol = symbolString[index]
		if symbol == '(':
			s.push(symbol)
		else if symbol == ")":
			if s.isEmpty():
				check = False
			else:
				s.pop()		## 如果栈里有左括号，就“匹配”掉，即pop掉栈顶的元素
		index += 1
	if check and s.isEmpty():	## 检验匹配完所有的右括号后，栈里是否还有剩余的左括号
		return True
	else:
		return False

当然通常情况下，可能不止要匹配左右括号，还要匹配左右方括号或者大括号等，我们把上述代码做一个改进：

def matches(open, close):
	opens = "([{"
	closes = ")]}"
	return opens.index(open) == closes.index(close)

def strCheck(symbolString):
	s = stack()
	check = True
	index = 0
	while index < len(symbolString) and check:
		symbol = symbolString[index]
		if symbol in '([{':
			s.push(symbol)
		elif symbol in ")]}":
			if s.isEmpty():
				check = False
			else:
				top = s.pop()		
				if not matches(top, symbol):
					check = False
		index += 1
	if check and s.isEmpty():	
		return True
	else:
		return False

print(strCheck("print(i dont like it)"))

2.2.4 十进制转换

在将十进制进行转换时，一般是用取余法，例如转换为二进制时：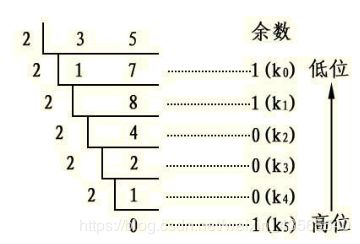
这里会发现：先得到的余数最后输出，很自然地，我们用栈来存储取余运算的结果。

def divideBy2(decNumber, base):
	remstack = Stack()

	digits = "0123456789ABCDEF"

	while decNumber > 0:
		rem = decNumber % base
		remstack.push(rem)
		decNumber = decNumber // base

	newString = ""
	while not remstack.isEmpty():
		binString = binString + str(digits[remstack.pop()])

	return newString

2.2.4 表达式转换

通常所用的表达式表达方法都为中缀表示法，但是这种方法存在混淆的可能，常用的解决方法为（1）引入操作符优先级的概念；（2）引入括号表示强制优先级。
但在计算机中最好能够明确所有的计算顺序，也就是避免引入操作符优先级的概念，由此引入全括号表达式：在所有表达式两边都加上括号。

全括号表达式以外，再通过移动符号的位置得到前缀表达式和后缀表达式。
前缀表达式：操作符 + 第一运算数 + 第二运算数。如 $A+B\ast C$写成$+A\ast BC$,$(A+B)\ast C$写成$+ABC$
后缀表达式：第一运算数 + 第二运算数 + 操作符

前缀表达式和后缀表达式中不再需要括号来明确优先级，操作符的次序完全决定了运算的内容，即离操作数越近的操作符越先做。
实际上表达式在计算机内部的表示方法就是前缀表示或后缀表示法。

现在需要解决如何用成套的算法来描述该过程：

1. 将中缀表达式转换为全括号形式
2. 将所有的操作符移到子表达式所在的左括号（前缀）或右括号（后缀）处，并将其替代，然后再删除所有的括号

2.2.5 习题

习题1：给定一个只包括(){}[]和空格的字符串，判断该字符串是否有效

## 用Python实现ADT Stack
class Stack():
	def __init__(self):
		self.items = []

	def isEmpty(self):
		return self.items == []

	def push(self, item):
		self.items.append(item)

	def pop(self):
		return self.items.pop()

	def peek(self):
		return self.items[-1]

	def size(self):
		return len(self.items)

def matches(open, close):
	opens = "([{"
	closes = ")]}"
	return opens.index(open) == closes.index(close)

def check(newstring):
	s = Stack()
	pos = 0
	check = True

	while pos < len(newstring) and check:
		symbol = newstring[pos]
		if symbol in "([{":
			s.push(symbol)
		else:
			if s.isEmpty():
				check = False
			else:
				top = s.pop()
				if not matches(top,symbol):
					check = False
		##print(check)
		pos += 1

	if check and s.isEmpty():
		return True
	else:
		return False

print(check("()"))
### 本题本来用了newstring.split()方法，但是犯了个错误：
### split只会按照空格进行分割，不会将每个字符作为列表

习题2： 一维开心消消乐：输入一串字符，逐个消去相邻的相同字符对，如果字符全部被消完，则输出不带引号的"None"

def xiaoxiaole(string):
	s = Stack()
	pos = 0

	for i in string:
		if s.isEmpty():
			s.push(i)
		else:
			if s.peek() == i:
				s.pop()
			else:
				s.push(i)
	xxlist = []
	while not s.isEmpty():
		xxlist.append(s.pop())

## [::-1]的含义是从取从后向前的元素， [-1]是取最后一个元素， [:-1]是取切片
	return "".join(xxlist[::-1])

print(xiaoxiaole("aabbc"))

习题3：

def xipanzi(num):
	s = Stack()
	i = 0
	j = 0
	while i <= 10 and j <= 9:
		if not s.isEmpty() and int(num[j]) == s.peek():
			s.pop()
			j += 1
		else:
			s.push(i)
			i += 1

	if s.isEmpty():
		print("Yes")
	else:
		print("No")

## 本题解题思想有些奇怪，首先需要假定顾客都是按照正确的洗碗顺序得出的碗来取的
## 比如num[0] = 3，说明第一个顾客取得的碗是3，那么在此之前已经洗了4个碗
## 当取得的碗编号与当前编号不符时，说明洗碗工还没洗好碗，需要继续洗碗

2.3 队列

队列是指新数据项的添加总发生在一端（称为尾端rear），而现存数据项的移除总发生在另一端（称为首端front）。
相比于栈后进先出的特点，队列往往是先进先出。

2.3.1 队列的操作

用Python实现的代码如下：

class Queue():
	def __init__(self):
		self.items = []

	def isEmpty(self):
		return self.items == []

	def enqueue(self, item):
		self.items.insert(0, item)

	def dequeue(self):
		return self.items.pop()

	def size(self):
		return len(self.items)

注意在队列中，添加一项的复杂度为$O(n)$，弹出一项的复杂度为$O(1)$，而如果将队首和队尾反过来，则复杂度也会相反。这个复杂度与栈是不同的，对于栈来说，如果选择列表的尾部作为栈顶，则添加和删除项的复杂度都为$O(1)$

2.3.2 队列的应用1：击鼓传花问题

利用队列来判断击鼓传花问题中，队列经过若干次传递后，是否会只剩下一个人：

• 首先用一个队列来存放所有参加游戏的人
• 用“队首”的人出队，并且到“队尾”入队表示一次传递
• 当传递了num次后，将此时位于队首的人移除，不再入队，表示他出队
• 如此反复进行，直到队列中只剩下一个人为止

class Queue():
	def __init__(self):
		self.items = []

	def isEmpty(self):
		return self.items == []

	def enqueue(self, item):
		self.items.insert(0, item)

	def dequeue(self):
		return self.items.pop()

	def size(self):
		return len(self.items)


def hotPotato(namelist, num):
	simqueue = Queue()
	for name in namelist:
		simqueue.enqueue(name)

	while simqueue.size() > 1:
		for i in range(num):
			simqueue.enqueue(simqueue.dequeue())

		simqueue.dequeue()

	return simqueue.dequeue()

print(hotPotato(["bill","david","susan","jane","brad"],7))

2.4 双端队列

2.4.1 双端队列抽象数据类型的实现

class Deque():
	def __init__(self):
		self.items = []

	def isEmpty(self):
		return self.items == []

	def addFront(self, item):
		self.items.append(item)

	def addRear(self, item):
		self.items.insert(0, item)

	def removeFront(self):
		self.items.pop()

	def removeRear(self):
		self.items.pop(0)

	def size(self):
		return len(self.items)

2.4.2 双端队列的应用（1）：回文词判定

回文词判定的思路：把待判定的字符加入到双端队列中，然后从队首和队尾同时移除字符，判定字符是否相等即可。

def palchecker(aString):
	chardeque = Deque()

	for ch in aString:
		chardeque.addRear(ch)

	check = True

	while chardeque.size() > 1 and check:
		first = chardeque.removeFront()
		last = chardeque.removeRear()
		if first != last:
			check = False

	return check

2.5 无序表结构

以上的栈、队列、双端队列三种线性基本结构都是我们用Python内置的list数据类型实现的，这种列表数据类型提供了非常多的操作接口如append()``pop()等，但是并不是所有编程语言都会提供list数据类型，因此我们还需要考虑如何实现这种数据类型。

2.5.1 列表的含义及其操作

一般来说我们把数据项按照相对位置存放的数据集称作列表，有时候还特别地将其称为无序表。在这种数据结构中数据项只按照存放的位置来索引。

对于无序表，我们应当有如下操作：

2.5.2 用链表实现无序表

列表是以数据的相对位置定义的数据集，但是并不要求数据项在存储空间中也是连续的。因此一般只需要在数据项之间建立连接指向即可。
对于链表来说，实现的基本单元是节点，每个节点需要包含数据项本身，以及指向下一个节点的引用信息。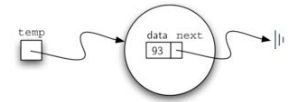
当引用信息为None时表明没有下一个节点，链表结束。
由于不需要按照顺序存储数据，所以链表在插入新数据时的时间复杂度为$O(1)$，但是查找节点或访问特点编号的节点需要$O(n)$（因为链表必须要遍历），而顺序表的复杂度则分别为$O(logn)$和$O(1)$。
接下来首先定义单链表节点类：

class Node():
	def __init__(self, data, next = None):
		self.data = data
		self.next = next

	def getData(self):
		return self.data

	def getNext(self):
		return self.next

然后实例化一下看看：

node1 = None	## node1是没有指向的节点对象
node2 = Node(1)	## node2的数据项为1，不指向下一个节点
node3 = Node('hello', node2)	## node3的数据项为2，指向节点node2

print(node1, node2.data, node2, node3.next, node3.next == node2)

从这4个输出结果可以看出一些东西：
node1的输出是None，这是无可争议的
node2.data的输出是1，因为node2存储的数据是1
node2的输出是它的地址
node3.next的输出时它指向的下一个节点，所以node3.next == node2的结果为True

当需要遍历整个列表的时候，首先需要找到第一个节点，然后依照该节点沿着链接遍历。因此还需要有对于第一个节点的引用：

class unorderedList():
	def __init__(self):
		self.head = None
		self.length = 0

	def demo(self):
		##创建链表示例
		for cnt in range(1, 10, 2):
			self.head = Node(cnt, self.head)
			self.length += 1
		return self.head

在创建链表时，需要保证链表的首项始终指向第一个节点，也就是说每有一个新的数据项，都是加在链表的表头。而无序列表本身并不包含数据项，因为数据项包含在节点中。

2.5.3 无序表的操作实现

• 打印链表中的所有内容：

def printunorderedList(self):
		temp = self.head
		while temp != None:
			print(temp.getData())
			temp = temp.getNext()

• 搜索目标值：

def search(self, item):
		temp = self.head
		check = False
		while temp != None and not check:
			if temp.data == item:
				check = True
			else:
				temp = temp.next
		return check

• 搜索目标项：

def index(self, num):
		temp = self.head
		while num > 1 and temp != None:
			temp = temp.next
			num -= 1
		return temp.data

• add方法，加在表头：
  由于链表结构若要遍历，则需要从头开始，因此从性能角度考虑，新的数据项最容易加入的位置应当是表头：

def add(self, item):
		temp = Node(item, self.head)
		self.head = temp

• size方法：
  取得链表size的方法通常是从表头遍历到表尾，且用变量累加经过的节点个数。

def size(self):
		current = self.head
		count = 0
		while current != None:
			count += 1
			current = current.getNext()
		return count

注意该方法的复杂度为$O(n)$

• 删除末尾项

def removeEnd(self):
		if self.head.next == None:
			self.head = None
		else:
			temp = self.head
			while temp.next.next != None:
				temp = temp.next
			temp.next = None

删除的时候需要注意，如果链表中只有一项的话，只需要把头设为None就可以了。同时还需要注意，下一个节点的引用信息是存储在当前节点中的。

• 删除任意位置的项

def removeAny(self, index):
		if index <= 0 or self.head.next == None:
			self.head = self.head.next
		else:
			temp = self.head
			while index > 1 and temp.next.next != None:
				temp = temp.next
				index -= 1
			temp.next = temp.next.next

• 删除指定项

def remove(self, item):
		temp = self.head
		previous = None
		check = False
		while not check:
			if temp.data == item:
				check = True
			else:
				previous = temp
				temp = temp.next

		if previous == None:
			self.head = temp.next
		else:
			previous.next = temp.next

那么我们把所有功能整合一下，写出一个完整的链表类及其实现：

# 先定义节点类
class Node:
	def __init__(self, data, next = None):
		self.data = data
		self.next = next

# 定义链表类
class LinkList:
#1 初始化链表	
	def __init__(self):
		self.head = None
		self.length = 0
#2 用数组初始化链表
	def initlist(self, data):
		for i in data:
			self.head = Node(i, self.head)
			self.length += 1

#3 输出链表内容
	def printList(self):
		temp = self.head
		while temp != None:
			print(temp.data)
			temp = temp.next

#4 向链表中添加内容，
## 因为链表需要遍历，从性能角度考虑，新加入的数据项放在表头比较好
	def add(self, data):
		temp = Node(data, self.head)
		self.head = temp
		self.length += 1

#5 删除末尾项
	def removeEnd(self):
		if self.head.next == None:
			self.head = None
		else:
			temp = self.head
			while temp.next.next != None:
				temp = temp.next
			temp.next = None

#6 删除任意项
	def removeAny(self, index):
		if index <= 0 or self.head.next == None:
			self.head = self.head.next
		else:
			temp = self.head
			while index > 1 and temp.next.next != None:
				temp = temp.next
				index -= 1
			temp.next = temp.next.next

三、递归

3.1递归的特性

递归作为解决问题的一种方法，其精髓在于将问题进行横向分解，划分为规模更小的相同问题，并且持续分解直到问题规模小到可以用非常简单的方法直接解决。
在算法方面，递归方法的重要特征就是在算法流程中调用自身。
例如，我们要求一个列表的和，用递归的形式来解决：

def listSum(nums):
	if len(nums) == 1:
		return nums[0]
	else:
		return nums[0] + listSum(nums[1:])

在该问题的解决中，我们把列表求和分解成了更小规模的相同问题：将列表中的第一个数与剩下的所有数求和，并且对于最小规模问题（即列表中只剩下一个数）的情况，直接返回该数自身。

递归算法三定律：

对于“调用自身”这一说法可能会较难理解，其实只需要将其理解为“问题分解成了规模更小的相同问题”就可以了。

3.1.1 递归调用的实现

现场数据：包括要返回的函数名称，以及调用函数时所包含的参数（局部变量）
调用栈：当一个函数被调用时，系统会把调用时的现场数据压入调用栈。此时将现场数据称为栈帧。每次函数返回时，可以用栈帧中的数据来恢复现场。

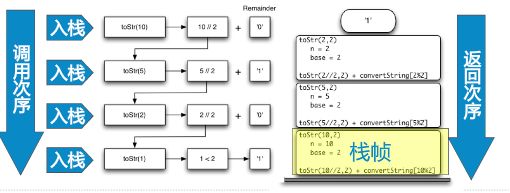
3.2 递归的应用

3.2.1 任意进制转换

我们之前说过十进制转换一般是用除法取余的方式，在那里是使用栈解决问题的：用栈储存每一次除法得到的余数，当被除数小于10时再将栈中的元素逐个弹出。
那么用递归解决该问题的方法为：

def toStr(n, base):
	convertString = "0123456789ABCDEF"
	if n < base:
		return convertString[n]
	else:
		return toStr(n // base, base) + convertString[n % base]

3.2.2 分型图形绘制

先介绍一下turtle库。
画一个五角星：

import turtle

t = turtle.Turtle()

t.pencolor('red')
t.pensize(3)

t.hideturtle()

for i in range(5):
	t.forward(100)
	t.right(144)

turtle.done()

用递归的方法画一个螺旋线：

def drawSpiral(t, linelen):
	if linelen > 0:
		t.forward(linelen)
		t.right(90)
		drawSpiral(t, linelen - 5)

drawSpiral(t, 100)

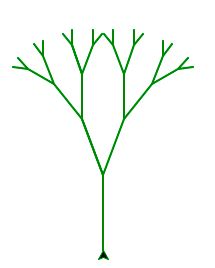
现在利用递归来绘制分型图形。所谓分型图形是指每个局部与整体相似的图形。

import turtle

t = turtle.Turtle()

def tree(branch_len):
	if branch_len > 5:
		t.forward(branch_len)
		t.right(20)
		tree(branch_len - 15)
		t.left(40)
		tree(branch_len - 15)
		t.right(20)
		t.backward(branch_len)

t.left(90)

t.pencolor('green')
t.pensize(2)
tree(75)
turtle.done()

最后画出来这样的小树苗。

3.2.3 汉诺塔问题

汉诺塔的规则不再赘述，这里主要说如何将汉诺塔问题分解成递归形式：

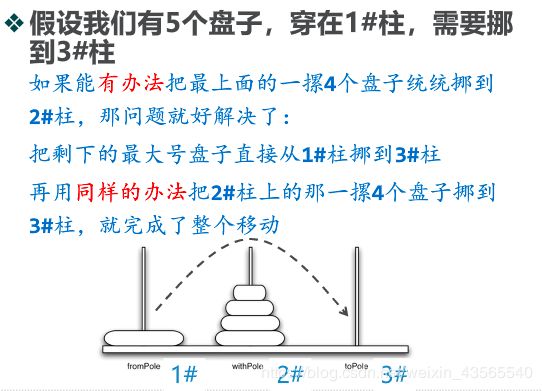
假设只有两个盘子（将上面4个盘子视作1个盘子），先将上面盘子移到2#，然后将下面盘子移到3#，再把上面盘子移到3#就可以了。
那么现在需要考虑的是如何把上面4个盘子移动到2#，其实可以使用相同的办法，即相当于现在一共只有4个盘子，目标柱是2#，那么再将4个盘子分解成最下面1个盘子和上面3个盘子，先将上面3个盘子移到3#，下面盘子移到2#，再将上面3个盘子移到2#就可以。于是现在的问题又转化为如何移动上面3个盘子，可以发现此时问题的规模就减小了。
因此递归流程可以写成如下形式：

def hanoTower(height, fromPole, withPole, toPole):
	if height >= 1:
		hanoTower(height - 1, fromPole, toPole, withPole)
		moveDisk(height, fromPole, toPole)
		hanoTower(height - 1, withPole, fromPole, toPole)
def moveDisk(disk, fromPole, toPole):
	print(f"moving disk[{disk}] from {fromPole} to {toPole}")

3.2.4 硬币找零问题

硬币找零问题中，我们的目标是找给顾客尽可能少的硬币。
那么根据递归三定律，首先确定基本结束条件：
需要对换的找零值恰好等于某个硬币的面值
然后确定减小问题规模的方法：
如果找零减去1分后，调用自身，即求兑换硬币最少数量 - 1
同理，如果找零减去25分后，调用自身，即求兑换硬币最少数量 - 25

def recMC(coinValueList, change):
	minCoins = change
	if change in coinValueList:
		return 1
	else:
		for i in [c for c in coinValueList if c <= change]:
			numCoins = 1 + recMC(coinValueList, change - i)
			if numCoins < minCoins:
				minCoins = numCoins
	return minCoins

本解法中出现了生成列表的推导式方法：

L = [x ** 2 for x in range(10)]

该方法可以生成x平方的列表。在这个语句中我们还可以加上if语句进行筛选：

L = [x for x in range(10) if x % 2 == 0]

那么在这种情况下只会保留偶数项。此外还可以嵌套使用for循环：

L = [x + y for x in 'ab' for y in 'jk']

此时会按照从左到右，从外层到内层的顺序进行遍历，生成列表。

那么以上这个算法算是解决问题了，但是它仍然有一个问题：存在大量重复计算，这个问题我们一般把计算好的中间结果保存起来，在每次递归之前先检查之前是否已经计算过。

def recDC(coinValueList, change, knownResults):
	minCoins = change
	if change in coinValueList:
		knownResults[change] = 1
		return 1
	elif knownResults[change] > 0:
		return knownResults[change]
	else:
		for i in [c for c in coinValueList if c <= change]:
			numCoins = 1 + recDC(coinValueList, change - i, knownResults)
			if numCoins < minCoins:
				minCoins = numCoins
				knownResults[change] = minCoins
	return minCoins

---

3.3 重新理解递归和动态规划

看到这里实际上感觉还不是很清楚。因此我补充看了较多的博客文章，主要有：

https://blog.csdn.net/m0_37907797/article/details/102767860
https://blog.csdn.net/u013309870/article/details/75193592
https://blog.csdn.net/baidu_28312631/article/details/47418773

结合之前所说的递归三定律，可以知道要写出一个递归程序，需要了解以下三点：

1. 明确函数的目的
2. 确定递归结束的条件
3. 确定递归规模减小的函数等价关系式

比如我们要写一个阶乘的函数，那么首先定义一个函数，并且明确它的目的就是求阶乘的结果：

def f(n):

确定递归结束的条件，所谓结束的条件就是当参数为何值时，可以直接知道函数的结果：

def f(n):
	if n == 1:
		return 1

最后一步就是要确定能够使递归规模减小的函数等价式，比如这里我们知道f(n)表示n个数的阶乘结果，那么f(n-1)就是n-1个数的阶乘结果，于是可以写成$f(n)=n\ast f(n-1)$，从而可以写出完整的递归函数：

def f(n):
	if n == 1:
		return 1
	else:
		return n * f(n-1)

以上就是阶乘递归函数的写法，接下来换一个例子：小青蛙跳台阶。假设一只青蛙一次可以跳上1级台阶，也可以跳上2级台阶，求问该青蛙跳上n级台阶共有多少种跳法？
按照程序来，首先定义一个函数，并且确定这个函数是计算跳上n级台阶的跳法的：

def f(n):

然后确定递归结束的条件：如果n = 1时，显然只有一种跳法，n=2时，有两种跳法（连跳两次1个台阶，或者跳一次2个台阶）

def f(n):
	if n <= 2:
		return n

最后确定使得函数规模减小的递推式：已知f(n)表示有n级台阶时的跳法，考虑小青蛙最开始的一跳，可能跳1阶，也可能跳2阶。如果跳1阶，那么剩下n-1个台阶，如果跳2阶，那么剩下n-2个台阶。所以可以知道$f(n)=f(n-1)+f(n-2)$。于是可以完成我们的递归函数：

def f(n):
	if n <= 2:
		return n
	else:
		return f(n-1) + f(n-2)

在这个递归过程中，我们会遇到一个重复计算的问题，对于这种问题，常用的解决方法是将已有的计算结果存储起来，当需要再次计算时，检查是否已经计算过，如果计算过，直接取出结果就行。

def f(n, knownResults):
	if n <= 2:
		return n
	else:
		if knownResults[n] != n:
			return knowResults[n]
		else:
			knownResults[n] = f(n-1) + f(n-2)
			return knownResults[n]

以上介绍了递归方法和能够优化递归的备忘录方法，现在来介绍一下由递归演化而来的动态规划方法。
首先动态规划英文名Dynamic Programming，实际上与动态和规划的关系都不大，倒不如说是对递归的一种优化方法。programming也是指决策而非编程。
其次需要明确哪些问题能够使用动态规划解决：

1. 问题的答案依赖于问题的规模，即所有问题的答案组成了一个数列
2. 大规模问题的答案可以由小规模问题的答案递推得到，即可以写出一个状态转移方程。

一般来说DP方法比递归方法的效率更高。比如对于上述青蛙爬楼梯问题，用DP方法解决应当是：

def f1(n):
	a = [0]*(n+1)
	a[1] = 1
	a[2] = 2
	
	if n <= 2:
		return n
	else:
		for i in range(3, n + 1):
			a[i] = a[i-1] + a[i-2]
	return a[n]

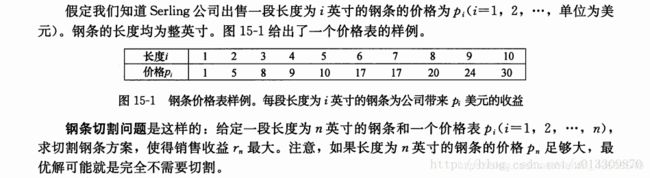
再举一些例子来说明，下面的例子是《算法》一书中的“钢条切割”问题：

首先用递归的方法解决这个问题：
递归方法解决问题的思路：确定问题的边界条件：当长度被切割到0的时候，收益为1。
然后倘若f(n)能够返回当长度为n的时候的最大收益，那么f(n-i)可以返回长度为n-i时的最大收益，于是我们可以把钢管切割成两段，第一段长度为i，第二段长度为n-i，然后只切割第二段，最后将所有的可能都进行比较：

def cut(n, price_dic):
		
	max_price = price_dic[n]
	
	if n == 0:
		return 0
	else:
		for i in range(1, n + 1):
			temp = price_dic[i] + cut(n-i, price_dic)
			if temp > max_price:
				max_price = temp
	return max_price

当然这种方法的缺点就是：重复计算太多！用DP方法求解：

def cut_buttom(n, price_dic):
	p = [0] * (n+1)
	p[0] = 0
	for i in range(1, n + 1):
		for j in range(i+1):
			p[i] = max(p[i], price_dic[j] + p[i-j])
	return p[n]

其中用到了两个循环，最内层循环保留在长度为i时的最优收益。
一般来说适用于动态规划解决的问题都具有以下两个特点：

• 最优子结构
  即一个问题的解结构包含了它子问题的最优解，则将该问题称为具有最优子结构性质
• 重叠子问题
  如果使用递归算法时有很多重复计算的问题，反复求解相同的子问题而没有新的子问题生成，则该问题具有重叠子问题的性质。一般在DP中使用数组保存子问题的解。