瘟疫模拟——群体建模专题设计第一阶段

瘟疫模拟——群体建模专题设计

主题

“瘟疫”主题的群体行为建模
第一阶段 技术预演与方案设计

新型冠状肺炎特征

关于新冠肺炎的一切 （回形针科普视频）：

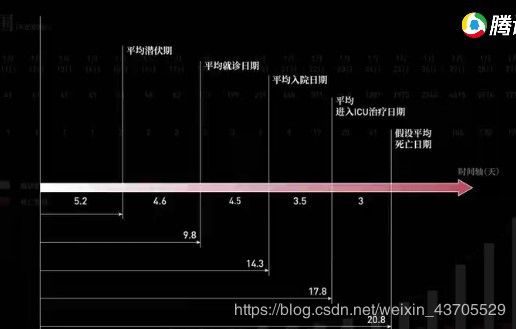
新型冠状病毒的受体和SARS一样，都是血管紧张转化酶2，病毒要感染人类，需要与有这种酶的细胞完成受体结合，而我们的身体中有不少这种细胞都暴露在空气中，于是大大增加了人体被感染的风险。黏膜感染、空气传播是冠状病毒非常容易传播的原因，喷嚏、咳嗽或仅是平静地说话都会产生数量很多的飞沫，造成病毒传播。根据1月30日《柳月刀》杂志发表的论文，对于武汉前425名确诊患者的分析，得出病毒的潜伏期平均为5.2天，从发病到就诊平均为4.6天，从就诊到入院平均为4.5天，从入院到转入ICU平均为3.5天，从ICU到假设死亡平均为3天。且病毒在早期已出现明显的人传人特征。根据以上的特征我们可以初步总结出病毒传播的一些时间节点和传播方式，分析出病毒传播的速率用于疫情模拟的模型建立。

相关知识

疫情数据可视化
数据可视化是将抽象概念进行形象性表达，将抽象语言进行具象图形可视的过程。让数据富有趣味性，使人们能够更好的复杂的数据。
1、 数据可视化展现自我隔离对于流行病疫情的控制。（processing）
2、疫情的流图 （每一个省的城市，都集合在一个圆圈里。病例总量多的城市圆圈就越大。每个城市的位置，根据容器图的算法，按照空间面积自动分配。）
3、 计算机仿真程序告诉你为什么现在还没到出门的时候！！！（源码: https://github.com/KikiLetGo/VirusBroadcast）

传染病模型及相关知识

SI模型

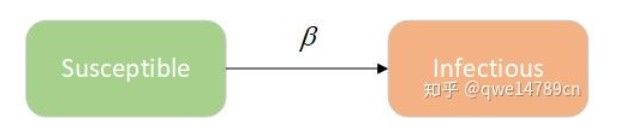
把人群分为2种,一种是易感者(Susceptibles)，即健康的人群，用S表示其人数，另一种是感染者(The Infected)，即患者，人数用I来表示。我们假设一个区域内总人数是N，即N=S+I，

有I个感染者整天到处溜达，每天碰到r个人，有β的概率会传染疾病，健康人比例为S/N，将以上所有量相乘就是每天新增感染病例，其微分方程形式方程如下：
dI/dt=rβIS/N
dS/dt=-rβIS/N
上述公式为马尔科夫链，又称离散时间马尔可夫链。此式表明当天的感染情况只和前一天的疾病感染人数有关。第N天的的人数我们可以表示为

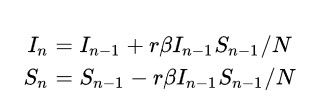
在matlab中可建立对应模型：

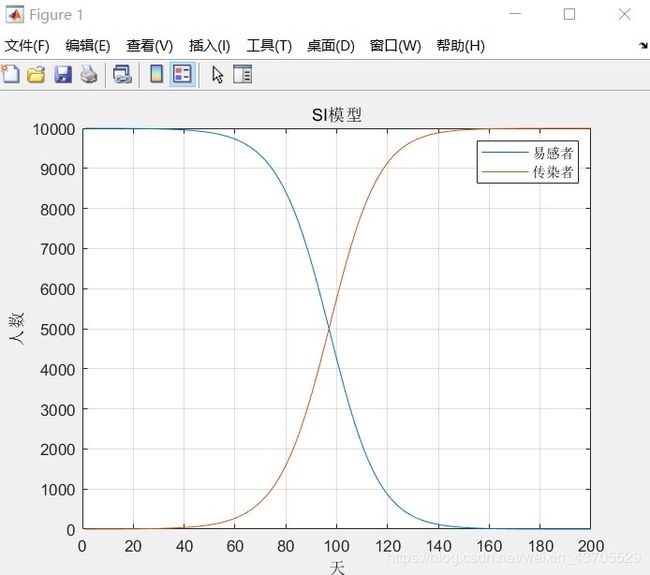
也就是对传染者不实施隔离，传染者到处走，一段时间后所有人都会被感染。

马尔科夫链

为状态空间中经过从一个状态到另一个状态的转换的随机过程。该过程要求具备“无记忆”的性质：下一状态的概率分布只能由当前状态决定，在时间序列中它前面的事件均与之无关。用一句话来概括马尔科夫链的话，那就是某一时刻状态转移的概率只依赖于它的前一个状态。用数学公式来表示就是：

举一个实例: 如图为一个股市模型

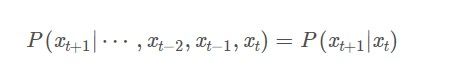
每一个状态都以一定的概率转化到下一个状态。因此可以得到马尔科夫链模型的状态转移矩阵为：

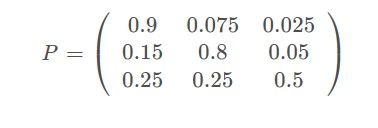
通过此状态转移矩阵发现，不管我们的初始状态是什么样子的，只要状态转移矩阵不发生变化，当n→∞时，最终状态始终会收敛到一个固定值。

细致平衡条件：给定一个马尔科夫链，分布Π和概率转移矩阵P，如果下面等式成立:
πiPij=πjPjiπiPij=πjPji ，则此马尔科夫链具有一个平稳分布（Stationary
Distribution)。

SIR模型

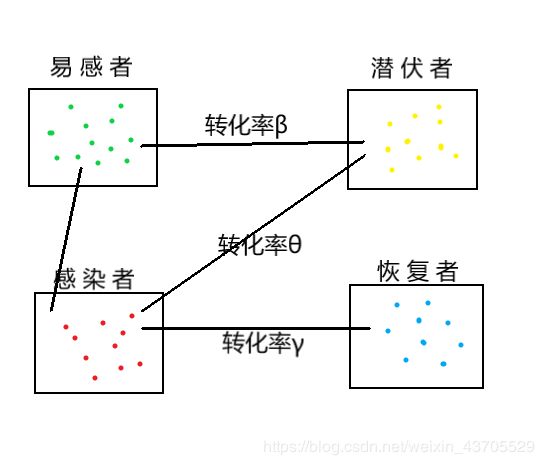
SIR模型是传染病模型中最经典的模型。SIR模型关注三类人群数量，即易感染人数、感染人数、康复人数，如图 1 所示，SIR 模型主要通过两个参数来调整三类人群的转换，从而模拟疾病的传播感染和康复过程。

设总人口为N(t)，则有N(t)=S(t)+I(t)+R(t)。

SIR模型的建立基于以下三个假设：
⑴不考虑人口的出生、死亡、流动等种群动力因素。人口始终保持一个常数，即N(t)≡K。
⑵一个病人一旦与易感者接触就必然具有一定的传染力。假设 t 时刻单位时间内，一个病人能传染的易感者数目与此环境内易感者总数s(t)成正比，比例系数为β，从而在t时刻单位时间内被所有病人传染的人数为βs(t)i(t)。
⑶ t 时刻，单位时间内从染病者中移出的人数与病人数量成正比，比例系数为γ，单位时间内移出者的数量为γi(t)。

基于以上三个假设条件，感染机制如下所示：

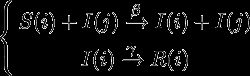
在以上三个基本假设条件下，可知：当易感个体和感染个体充分混合时，感染个体的增长率为βi（t)s(t)-γi(t)，易感个体的下降率为βi（t)s(t)，恢复个体的增长率为γi(t)。
易感者从患病到移出的过程可以用微分方程表示如下：

解得微分方程的解为

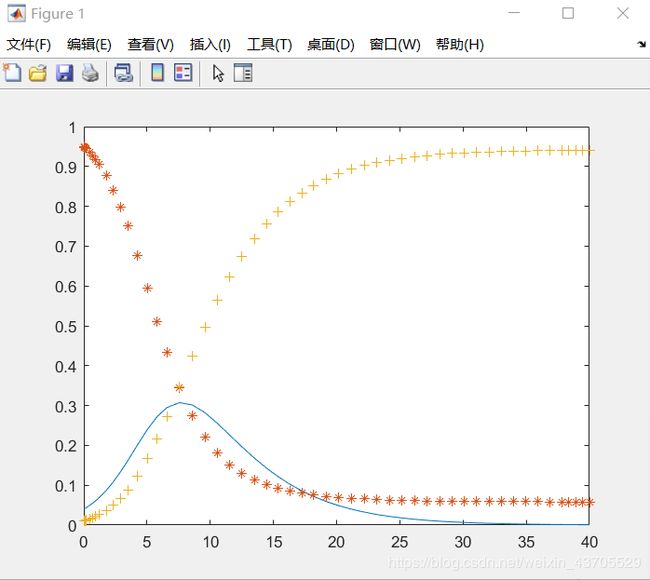
分析SIR传染病模型，也就是三个微分方程，在matlab中可以建立如下模型：

红线代表易感者，蓝线代表传染者，黄线代表康复者

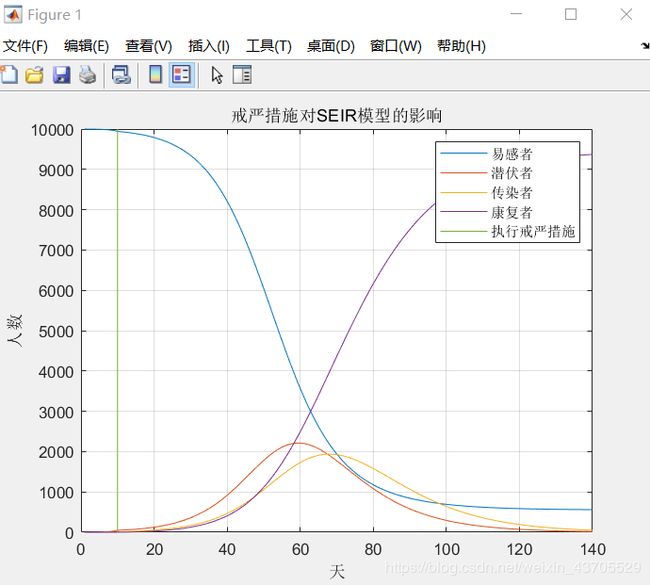
按照这个模型，感染者在传播初期会迎来一个峰值，随着治疗康复的人越来越多，感染者下降，拥有抗体的人数不断增多，病情得到控制，感染者人数减少。

SEIR模型

实际情况更加复杂，易感染人群在一开始会经历潜伏期，一段时间之后才出现症状，因此SEIR模型为在SIR模型的基础上引入潜伏者，潜伏者按照概率α转化为感染者。

SEIR模型的微分方程如下：

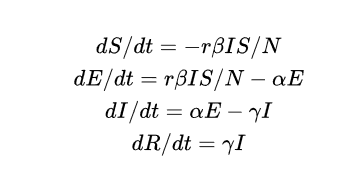
修改迭代形式为：

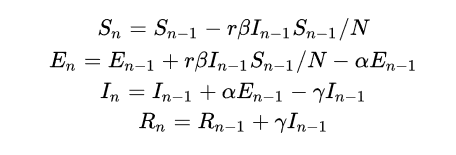
在matlab中可建立在SIR模型基础上修改得到的SEIR模型：

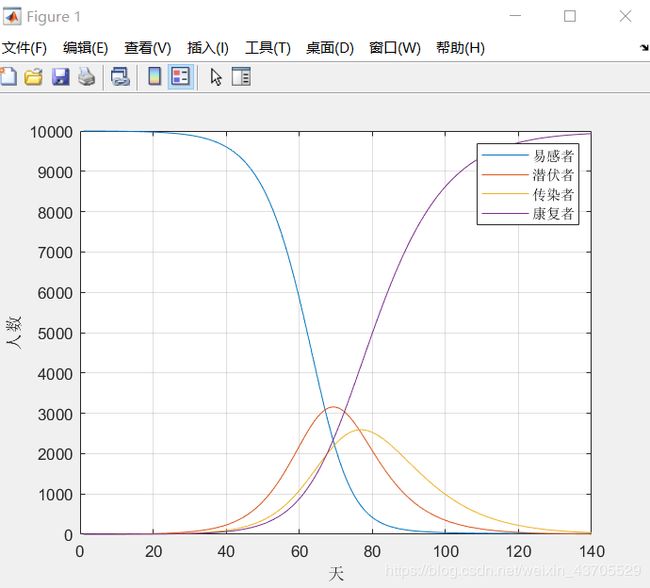
和SIR模型相似，注意到潜伏者数量也是先增加后减少。

病毒潜伏期具有传染性，因此我们要引入潜伏者的传染概率为β2可以将健康的易感者转变为潜伏者。而潜伏者每天接触的健康易感者人数为r2。在dS/dt和dE/dt后添加潜伏者对易感健康人群S传染概率β2和接触人数r2，让更多正常人变为潜伏者，微分方程如下:

修改后的迭代方程：

修改之后的SEIR模型:

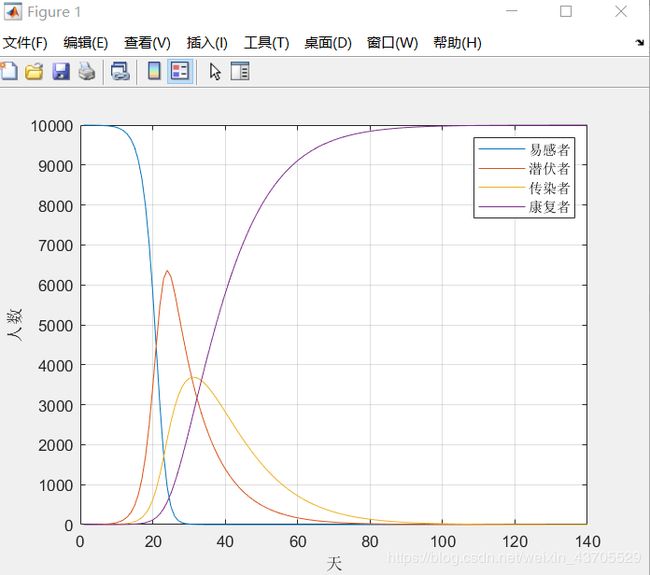
戒严后的SEIR模型:

细胞自动机

细胞自动机是为模拟包括自组织结构在内的复杂现象提供的一个强有力的方法，也称为元胞自动机。

根据《代码本色》第六章自制智能体的内容，研究转向力、到达行为等知识，创建出细胞自动机模型。一维细胞自动机的概念与二维细胞自动机没有什么不同，但是当从一行细胞开始，在下一个标有记号的地方时，该行就会被一个遵循一定规则的新行替换。可以根据细胞的颜色、与之相邻的其他两个细胞以及它下面新细胞的颜色来指定规则。例如模式：

指定一个规则，如果某个细胞为白色且与之相邻的细胞中有两个为黑色，则此细胞下面的细胞也应为黑色。由于相邻细胞只有八种可能的情况，我们只需要列出八个中每一个细胞是黑色还是白色，一个完整的规则就可以确定在任何情况下细胞可能出现的情况。通过将黑色设为1，白色设为0，你可以为每个相邻模式标记从0到7之间的数字，然后将下一行的黑色或白色细胞看作八个0或八个1读取，即二进制数。这可以用作指定规则的索引。

草图实验设计

群体免疫

背景是一座人口密集的城市，疫情大规模爆发，但政府不采取任何防疫措施，选择群体免疫的方法，即病毒传播到一定程度时，部分体内产生抗体的人可以存活下来。一开始对感染者不加以限制，四处游走，病毒传染给易感者，导致易感者变为感染者，符合SI模型，感染者剧增。一段时间后，部分人体内产生抗体，恢复者的数量有所上升，但是感染者的数量应该还是远远高于易感者和恢复者，类似SIR模型，但是传染者的峰值应该会出现得较晚，峰值的数量也会很高。

2、基于SEIR模型疫情模拟

疫情爆发，病毒具有潜伏期，但潜伏期仍有传染性，还有无症状感染者的情况。易感者有几率变为潜伏者和感染者，潜伏期过了之后，潜伏者变为感染者，感染者一部分恢复，一部分死去，以这样的规律移到对应的框中。
设计不同的措施对于疫情的影响 ：

（1）、实施限制出门，强制戴口罩等措施，鼓励在家办公，大型公共场合每日做好消杀工作，易感者变为感染者或潜伏者的转化率就降低一些。

（2）、集中医疗资源，加强对病人的隔离救治，感染者转化为恢复者的转化率提高。

参考资料

关于新冠肺炎的一切｜回形针 https://v.qq.com/x/cover/mzc00200pj7r8zs/y3059qtik2o.html

SI/SEIR模型介绍 https://zhuanlan.zhihu.com/p/104268573?night=1

SIR模型介绍 https://baike.baidu.com/item/SIR模型/1938321?fr=aladdin

小白都能看懂的马尔科夫链详解https://blog.csdn.net/bitcarmanlee/article/details/82819860

一文读懂细胞自动机的起源

https://www.360kuai.com/pc/99ad64800d5d0cfa7?cota=4&sign=360_57c3bbd1&refer_scene=so_1