python机器学习引入-附:kaggle房价预测代码
本文的代码为了实现 预测房屋价格
开始之前
-
建议安装一个 jupyter notebook(用来测试学习非常便利,当然直接在pycharm 里面也同样可以)
-
我的python版本:python 3.7
-
训练数据下载地址1: kaggle房价预测数据
-
训练数据下载地址2: kaggle房价预测数据
-
参考资料:万门开启你的人工智能第一课的部分笔记
-
文章图片来自网络-侵权删
-
解决no module named XXX (一直解决不了直接看方法四) 添加链接描述
模型详解(预测价格)
in
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from IPython.display import Image
import warnings
warnings.filterwarnings('ignore')
%matplotlib inline
data = pd.read_csv('C:/code/train_data/hourse6965/train.csv')
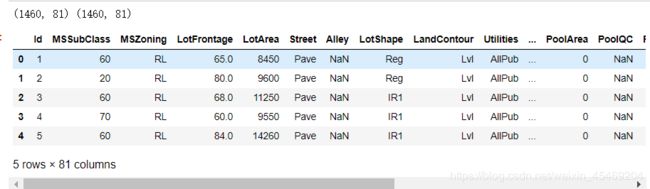
print(data.shape,data.shape)
data.head()
数据预处理
数太大,归一化,让数据的分布处于同一区间,我们选择一种最简单的数据调整方法,每个数除以其最大值
in
# 选择数据集合中的几个重要特征
data_select = data[['BedroomAbvGr','LotArea','Neighborhood','SalePrice']]
# 重命名
data_select = data_select.rename(columns={'BedroomAbvGr':'room','LotArea':'area'})
# 对缺失的数据进行过滤
data_select = data_select.dropna(axis = 0)
# np.take(data_select.columns,[0,1,3])
for col in np.take(data_select.columns,[0,1,-1]):
# print(data_select[col].max())
data_select[col] /= data_select[col].max()
# print(data_select[col].max())
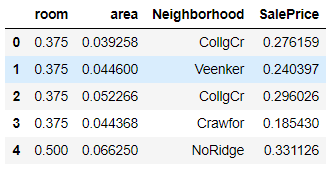
data_select.head()
np.take(data_select.columns,[0,1,3])
out
Index([‘room’, ‘area’, ‘SalePrice’], dtype=‘object’)
数据分为:训练集和测试集
对上面的方法简单封装
in
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from IPython.display import Image
import warnings
warnings.filterwarnings('ignore')
%matplotlib inline
# 尝试封装数据处理
def data_process(data):
# 选择数据集合中的几个重要特征
data_select = data[['BedroomAbvGr','LotArea','Neighborhood','SalePrice']]
# 重命名
data_select = data_select.rename(columns={'BedroomAbvGr':'room','LotArea':'area'})
# 对缺失的数据进行过滤
data_select = data_select.dropna(axis = 0)
for col in np.take(data_select.columns,[0,1,-1]):
data_select[col] /= data_select[col].max()
return data_select
out
in
# 训练数据
train_data = pd.read_csv('C:/code/train_data/hourse6965/train.csv')
train = data_process(data=train_data)
data_select = data_process(data=train_data)
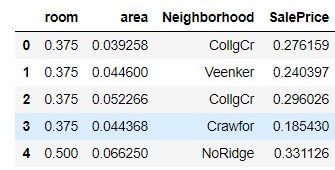
train.head()
in
# 测试数据和训练数据
from sklearn.model_selection import train_test_split
train, test = train_test_split(data_select.copy(),test_size = 0.9)
out
in
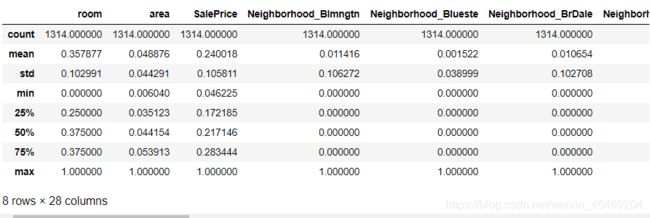
test.describe()
构建模型
线性回归模型
从最简单的情况出发,构建一台预测价格的机器,假设 h(x) = wx + b 是线性的.
in
def linear(features, pars):
price = np.sum(features*pars[:-1],axis = 1) + pars[-1]
return price
out
模型测试
试一试你的模型预测价格和真实价格作比较
in
train['predict'] = linear(train[['room','area']].values,np.array([0.1,0.1,0.0]))
train.head()
out
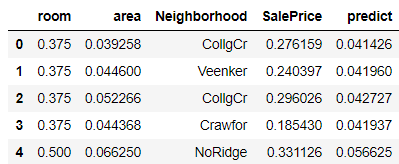
可以看到,在该参数下,模型的预测价格和真实价格有较大的差距.那么寻找合适的参数值是我们需要做的事情
代价函数
预测函数为 h(x) = wx + b
度量预测错误, 代价函数是误差的平方和.

in
def mean_squared_error(y_pred, y):
return sum(np.array(y_pred - y) **2)
def Cost(df, features, pars):
df['predict'] = linear(df[features].values, pars)
cost = mean_squared_error(df.predict, df.SalePrice)/len(df)
return cost
cost=Cost(train,['room','area'],np.array([0.1,0.1,0.1]))
print(cost)
out
0.015972537582855502
暴力搜索
假设模型的截距顶b = 0
in
Xs = np.linspace(0,1,100)
Ys = np.linspace(0,1,100)
Zs = np.zeros([100,100])
Xs,Ys = np.meshgrid(Xs,Ys)
Xs.shape , Ys.shape
out
((100, 100), (100, 100))
in
W1 = []
W2 = []
Costs = []
for i in range(100):
for j in range(100):
W1.append(0.01*i)
W2.append(0.01*j)
Costs.append(Cost(train,['room','area'],np.array([0.01*i,0.01*j,0.])))
index = np.array(Cost).argmin()
print(W1[index],W2[index],Costs[index])
out
0.0 0.0 0.061567303630542546
in
from mpl_toolkits.mplot3d import Axes3D
fig=plt.figure()
ax = fig.add_subplot(111,projection='3d')
ax.view_init(5,-15)
ax.scatter(W1,W2,Costs,s=10)
ax.scatter(0.58,0.28, zs=Cost(train,['room','area'],np.array([0.58,0.28,0.0])),s=100,color='red')
plt.xlabel('rooms')
plt.ylabel('llotArea')
fig = plt.figure()
ax = fig.add_subplot(111,projection='3d')
ax.view_init(5,15)
ax.scatter(W1,W2,Costs,s=10)
ax.scatter(0.58,0.28, zs=Cost(train,['room','area'],np.array([0.58,0.28,0.0])),s=100,color='red')
plt.xlabel('rooms')
plt.ylabel('llotArea')
out
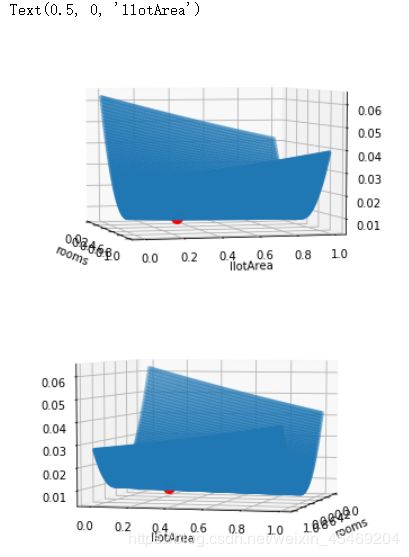
从中可以看出我们的格点搜索出来的点,确实具备有更小的Cost
梯度下降法
# pars 是w 和 b 的总和
def gradient(train,features, pars):
Gradint = np.zeros(len(pars))
for i in range(len(pars)):
pars_new = pars.copy()
pars_new[i] += 0.01
Gradint[i] = (Cost(train,features,pars_new)-Cost(train,features,pars))/0.01
return Gradint
gradint(train,['room','area'],[0.2,0.1,0])
out
array([-0.10885598, -0.01627349, -0.30192594])
in
# 梯度下降
def GradientDescent(data, epochs,lr, features, pars):
Costs = []
for i in range (epochs):
grad = gradient(train,features, pars)
if i%50 == 0 :
Costs.append(Cost(data,features, pars))
pars -= grad*lr
print('w=',pars)
return pars,Costs
out
in
pars,Costs = GradientDescent(train,500,0.002,['room','area'],[0.1,0.1,0])
out
w= [0.15554215 0.10906826 0.14727843]
查看梯度下降过程
in
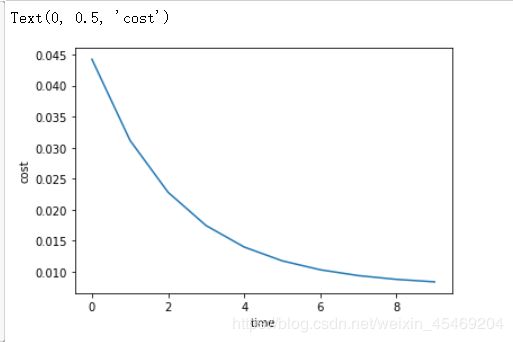
plt.plot(Costs)
plt.xlabel('time')
plt.ylabel('cost')
预测和模型评估
用学习出来的模型做预测
in
cost = Cost(train,['room','area'], pars)
cost
out
0.008117485926477354
查看预测的均方误差
in
from sklearn.metrics import mean_squared_error
train['predict'] = linear(train[['room','area']].values, pars )
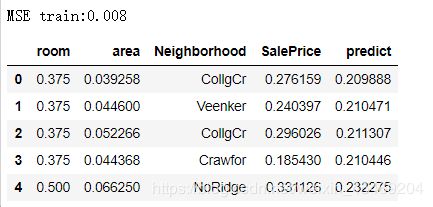
print('MSE train:%.3f'%(mean_squared_error(train['SalePrice'],train['predict'])))
train.head()
test['predict'] = linear(test[['room','area']].values,pars)
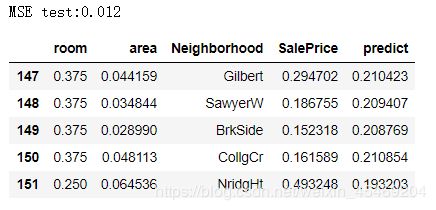
print('MSE test:%.3f'%(mean_squared_error(test['SalePrice'],test['predict'])))
test.head()
cost =Cost(test,['room','area'],pars)
cost
out
9.048258696669528e-06
如何做的更好
结果是否理想,能够如何优化,是否存在一个模型,使得误差为0 ? 增加特征试一试我们把之前的模型封装起来,并且使用公式运算梯度,比较一下和之前的速度差别!
in
class LinearRegressionGD(object):
def __init__(self, eta=0.001,n_iter=20):
self.eta = eta
self.n_iter = n_iter
def fit(self,X,y):
self.w_ = np.zeros(1+X.shape[1])
self.cost_ = []
for i in range(self.n_iter):
output = self.net_input(X)
errors = (y - output)
self.w_[:-1] += self.eta * X.T.dot(errors)
self.w_[-1] += self.eta * errors.sum()
cost = (errors**2).sum()/2.0
self.cost_.append(cost)
return self
def net_input(self, X):
return np.dot(X, self.w_[:-1])+ self.w_[-1]
def predict(self, X):
return self.net_input(X)
out
in
# 测试数据和训练数据在前面获得的
data_select=pd.get_dummies(data_select)
train, test = train_test_split(data_select.copy(),test_size = 0.9)
train_ = train.copy()
train_y =train_.pop('SalePrice')
train_x =train_
test_ = test.copy()
test_y = test_.pop('SalePrice')
test_x = test_
lr = LinearRegressionGD(n_iter = 1000)
lr.fit(train_x.values, train_y.values)
out
<main.LinearRegressionGD at 0x253bd9a48c8>
in
lr.w_
out
array([ 0.12242956, 0.09303798, 0.00586314, 0. , -0.07794866,
-0.03106852, 0. , 0.01659729, 0.01963676, -0.06752194,
0.00903525, -0.09960704, -0.04162748, -0.05640296, -0.05808563,
0. , 0.00492592, 0.27390849, 0.11189038, -0.08732825,
-0.07227152, -0.06557435, -0.01584715, 0.06369002, 0.20816382,
0.15481452, 0. , 0.19524208])
in
from sklearn.metrics import mean_squared_error
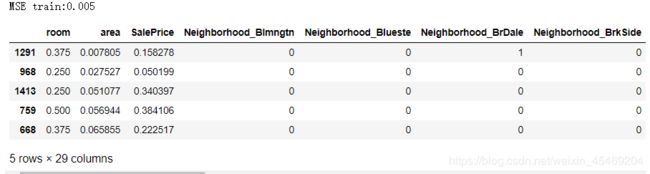
train['predict'] = lr.predict(train_x.values)
print('MSE train:%.3f' % (mean_squared_error(train_y, train['predict'])))
train.head()
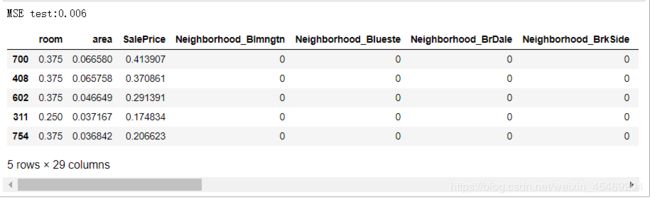
test['predict'] = lr.predict(test_x.values)
print('MSE test:%.3f'%(mean_squared_error(test_y,test['predict'])))
test.head()