Python之Matplotlib数据可视化(七):用Matplotlib画三维图
Python之Matplotlib数据可视化(七):用Matplotlib画三维图
- 1 三维数据点与线
- 2 三维等高线图
- 2.1 三维等高线图
- 2.2 调整三维图的观察视角
- 3 线框图和曲面图
- 3.1 线框图
- 3.2 三维曲面图
- 3.3 极坐标曲面图
- 4 曲面三角剖分
- 4.1 三维采样的曲面图
- 4.2 三角剖分曲面图
- 4.3 案例:莫比乌斯带
- 备注
Matplotlib 原本只能画二维图。大概在 1.0 版本的时候,Matplotlib 实现了一些建立在二维图基础上的三维图功能,于是一组画三维图可视化的便捷(尚不完美)工具便诞生了。我们可以导入 Matplotlib 自带的 mplot3d 工具箱来画三维图
from mpl_toolkits import mplot3d
导入这个子模块之后,就可以在创建任意一个普通坐标轴的过程中加入 projection='3d'关键字,从而创建一个三维坐标轴:
import numpy as np
import matplotlib.pyplot as plt
fig = plt.figure()
ax = plt.axes(projection='3d')

有了三维坐标轴之后,我们就可以在上面画出各种各样的三维图了。
1 三维数据点与线
最基本的三维图是由 (x , y , z ) 三维坐标点构成的线图与散点图。可以用 ax.plot3D 与 ax.scatter3D 函数来创建它们。由于三维图函数的参数与二维图函数的参数基本相同。下面来画一个三角螺旋线(trigonometric spiral),在线上随机分布一些散点
ax = plt.axes(projection='3d')
# 三维线的数据
zline = np.linspace(0, 15, 1000)
xline = np.sin(zline)
yline = np.cos(zline)
ax.plot3D(xline, yline, zline, 'gray')
# 三维散点的数据
zdata = 15 * np.random.random(100)
xdata = np.sin(zdata) + 0.1 * np.random.randn(100)
ydata = np.cos(zdata) + 0.1 * np.random.randn(100)
ax.scatter3D(xdata, ydata, zdata, c=zdata, cmap='Greens');
from mpl_toolkits import mplot3d
import numpy as np
import matplotlib.pyplot as plt
fig = plt.figure()
ax = plt.axes(projection='3d')
# 三维线的数据
zline = np.linspace(0, 15, 1000)
xline = np.sin(zline)
yline = np.cos(zline)
ax.plot3D(xline, yline, zline, 'gray')
# 三维散点的数据
zdata = 15 * np.random.random(100)
xdata = np.sin(zdata) + 0.1 * np.random.randn(100)
ydata = np.cos(zdata) + 0.1 * np.random.randn(100)
ax.scatter3D(xdata, ydata, zdata, c=zdata, cmap='Greens');
plt.show()

默认情况下,散点会自动改变透明度,以在平面上呈现出立体感。有时在静态图形上观察三维效果很费劲,通过交互视图(interactive view)就可以让所有数据点呈现出极佳的视觉效果。
2 三维等高线图
与二维等高线相比, mplot3d 有用同样的输入数据创建三维晕渲(relief)图的工具。与二维 ax.contour 图形一样, ax.contour3D 要求所有数据都是二维网格数据的形式,并且由函数计算 z 轴数值。
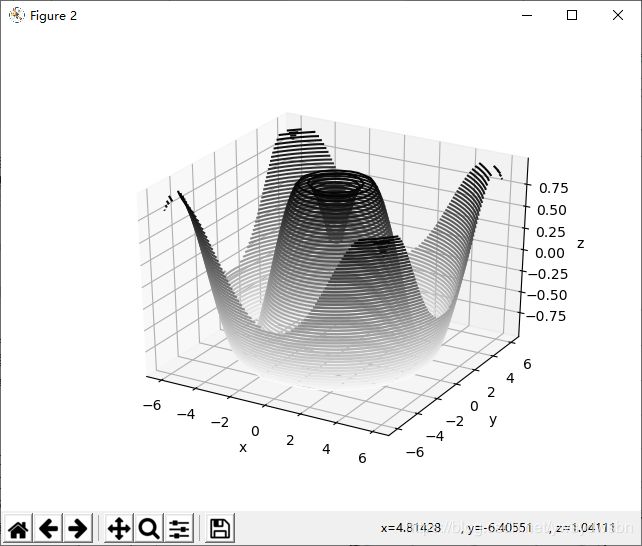
2.1 三维等高线图
下面演示一个用三维正弦函数画的三维等高线图
def f(x, y):
return np.sin(np.sqrt(x ** 2 + y ** 2))
x = np.linspace(-6, 6, 30)
y = np.linspace(-6, 6, 30)
X, Y = np.meshgrid(x, y)
Z = f(X, Y)
fig = plt.figure()
ax = plt.axes(projection='3d')
ax.contour3D(X, Y, Z, 50, cmap='binary')
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('z');
from mpl_toolkits import mplot3d
import numpy as np
import matplotlib.pyplot as plt
def f(x, y):
return np.sin(np.sqrt(x ** 2 + y ** 2))
x = np.linspace(-6, 6, 30)
y = np.linspace(-6, 6, 30)
X, Y = np.meshgrid(x, y)
Z = f(X, Y)
fig = plt.figure()
ax = plt.axes(projection='3d')
ax.contour3D(X, Y, Z, 50, cmap='binary')
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('z');
plt.show()
2.2 调整三维图的观察视角
默认的初始观察角度有时不是最优的, view_init 可以调整观察角度与方位角(azimuthal angle)。我们把俯仰角调整为 60 度(这里的 60 度是 x-y 平面的旋转角度),方位角调整为 35 度(就是绕 z 轴顺时针旋转 35 度):
ax.view_init(60, 35)
fig
from mpl_toolkits import mplot3d
import numpy as np
import matplotlib.pyplot as plt
def f(x, y):
return np.sin(np.sqrt(x ** 2 + y ** 2))
x = np.linspace(-6, 6, 30)
y = np.linspace(-6, 6, 30)
X, Y = np.meshgrid(x, y)
Z = f(X, Y)
fig = plt.figure()
ax = plt.axes(projection='3d')
ax.contour3D(X, Y, Z, 50, cmap='binary')
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('z');
ax.view_init(60, 35)
fig
plt.show()

其实,也可以在 Matplotlib 的交互式后端界面直接通过点击、拖拽图形,实现同样的交互旋转效果。
3 线框图和曲面图
还有两种画网格数据的三维图没有介绍,就是线框图和曲面图。它们都是将网格数据映射成三维曲面,得到的三维形状非常容易可视化。
3.1 线框图
下面是一个线框图示例
fig = plt.figure()
ax = plt.axes(projection='3d')
ax.plot_wireframe(X, Y, Z, color='black')
ax.set_title('wireframe');
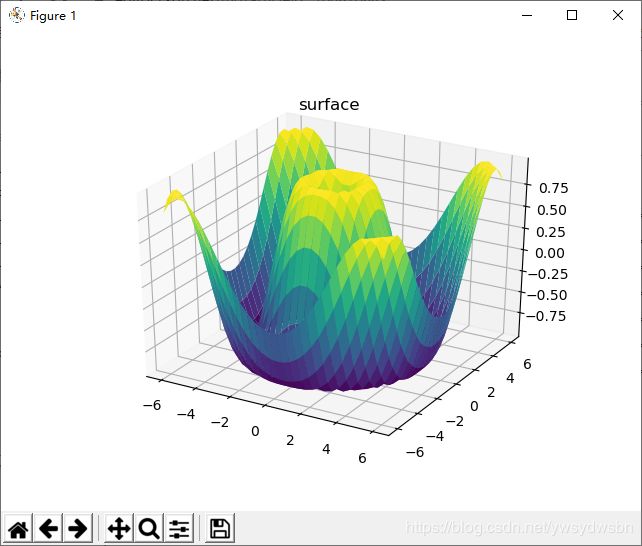
3.2 三维曲面图
曲面图与线框图类似,只不过线框图的每个面都是由多边形构成的。只要增加一个配色方案来填充这些多边形,就可以让读者感受到可视化图形表面的拓扑结构了
ax = plt.axes(projection='3d')
ax.plot_surface(X, Y, Z, rstride=1, cstride=1,cmap='viridis', edgecolor='none')
ax.set_title('surface');
from mpl_toolkits import mplot3d
import numpy as np
import matplotlib.pyplot as plt
def f(x, y):
return np.sin(np.sqrt(x ** 2 + y ** 2))
x = np.linspace(-6, 6, 30)
y = np.linspace(-6, 6, 30)
X, Y = np.meshgrid(x, y)
Z = f(X, Y)
fig = plt.figure()
ax = plt.axes(projection='3d')
ax.plot_surface(X, Y, Z, rstride=1, cstride=1,
cmap='viridis', edgecolor='none')
ax.set_title('surface');
plt.show()
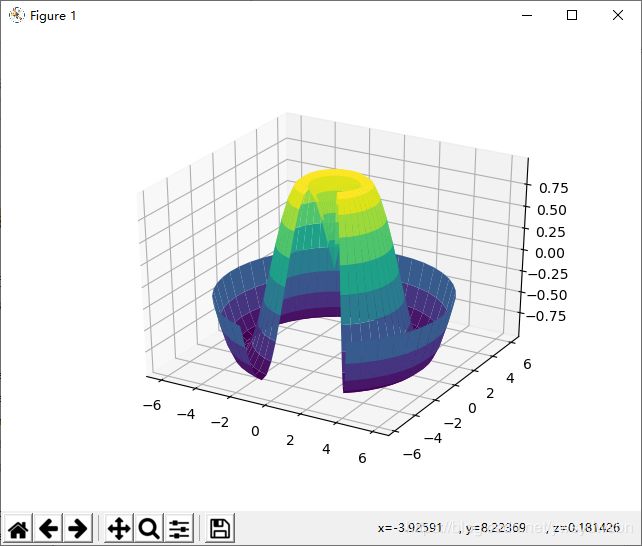
3.3 极坐标曲面图
需要注意的是,画曲面图需要二维数据,但可以不是直角坐标系(也可以用极坐标)。下面的示例创建了一个局部的极坐标网格(polar grid),当我们把它画成 surface3D 图形时,可以获得一种使用了切片的可视化效果
r = np.linspace(0, 6, 20)
theta = np.linspace(-0.9 * np.pi, 0.8 * np.pi, 40)
r, theta = np.meshgrid(r, theta)
X = r * np.sin(theta)
Y = r * np.cos(theta)
Z = f(X, Y)
ax = plt.axes(projection='3d')
ax.plot_surface(X, Y, Z, rstride=1, cstride=1,
cmap='viridis', edgecolor='none');
from mpl_toolkits import mplot3d
import numpy as np
import matplotlib.pyplot as plt
def f(x, y):
return np.sin(np.sqrt(x ** 2 + y ** 2))
r = np.linspace(0, 6, 20)
theta = np.linspace(-0.9 * np.pi, 0.8 * np.pi, 40)
r, theta = np.meshgrid(r, theta)
X = r * np.sin(theta)
Y = r * np.cos(theta)
Z = f(X, Y)
ax = plt.axes(projection='3d')
ax.plot_surface(X, Y, Z, rstride=1, cstride=1,
cmap='viridis', edgecolor='none');
plt.show()
4 曲面三角剖分
在某些应用场景中,上述这些要求均匀采样的网格数据显得太过严格且不太容易实现。这时就可以使用三角剖分图形(triangulation-based plot)了。如果没有笛卡尔或极坐标网格的均匀绘制图形,我们该如何用一组随机数据画图呢?
4.1 三维采样的曲面图
theta = 2 * np.pi * np.random.random(1000)
r = 6 * np.random.random(1000)
x = np.ravel(r * np.sin(theta))
y = np.ravel(r * np.cos(theta))
z = f(x, y)
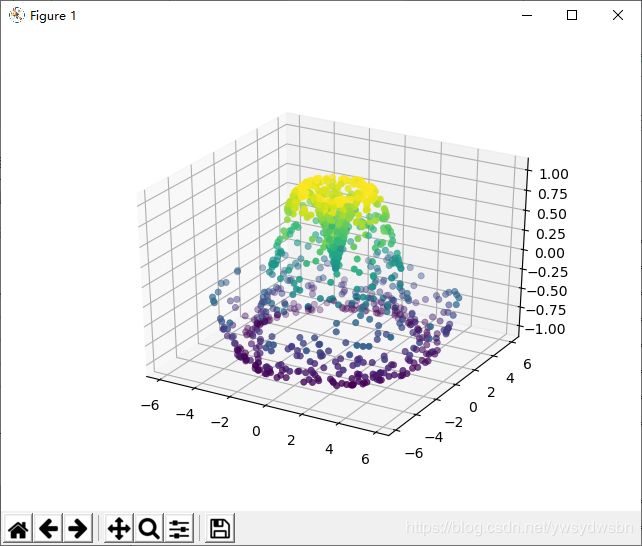
可以先为数据点创建一个散点图,对将要采样的图形有一个基本认识
ax = plt.axes(projection='3d')
ax.scatter(x, y, z, c=z, cmap='viridis', linewidth=0.5);
from mpl_toolkits import mplot3d
import numpy as np
import matplotlib.pyplot as plt
def f(x, y):
return np.sin(np.sqrt(x ** 2 + y ** 2))
theta = 2 * np.pi * np.random.random(1000)
r = 6 * np.random.random(1000)
x = np.ravel(r * np.sin(theta))
y = np.ravel(r * np.cos(theta))
z = f(x, y)
ax = plt.axes(projection='3d')
ax.scatter(x, y, z, c=z, cmap='viridis', linewidth=0.5);
plt.show()
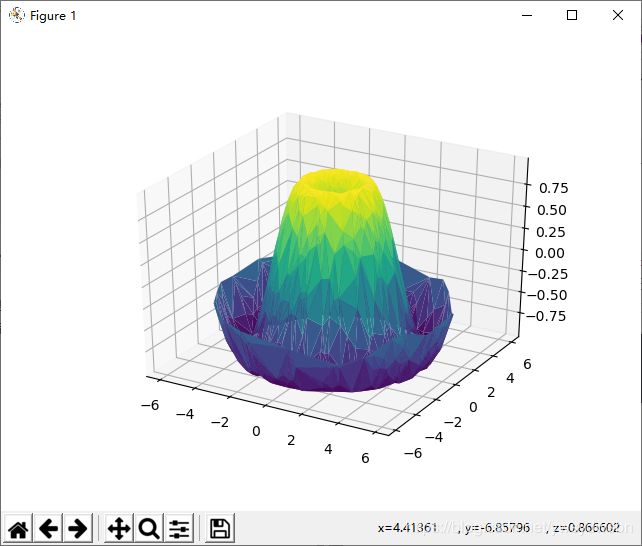
4.2 三角剖分曲面图
还有许多地方需要修补,这些工作可以由 ax.plot_trisurf 函数帮助我们完成。它首先找到一组所有点都连接起来的三角形,然后用这些三角形创建曲面(结果如图 所示,其中 x 、 y 和 z 参数都是一维数组):
ax = plt.axes(projection='3d')
ax.plot_trisurf(x, y, z,
cmap='viridis', edgecolor='none');
from mpl_toolkits import mplot3d
import numpy as np
import matplotlib.pyplot as plt
def f(x, y):
return np.sin(np.sqrt(x ** 2 + y ** 2))
theta = 2 * np.pi * np.random.random(1000)
r = 6 * np.random.random(1000)
x = np.ravel(r * np.sin(theta))
y = np.ravel(r * np.cos(theta))
z = f(x, y)
ax = plt.axes(projection='3d')
ax.plot_trisurf(x, y, z,
cmap='viridis', edgecolor='none');
plt.show()
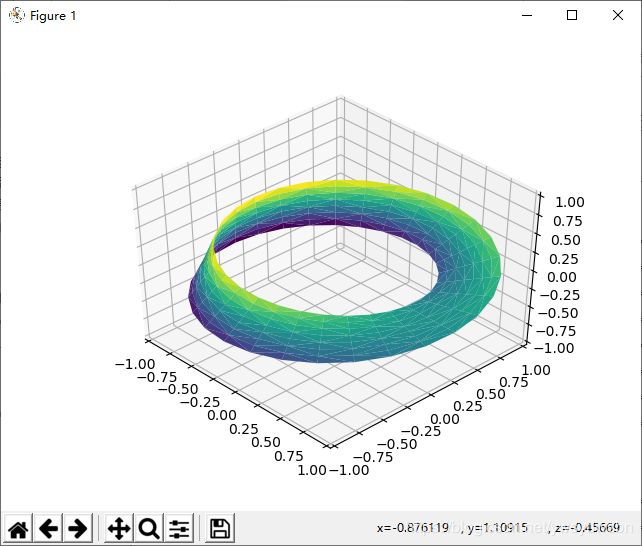
虽然结果肯定没有之前用均匀网格画的图完美,但是这种三角剖分方法很灵活,可以创建各种有趣的三维图。例如,可以用它画一条三维的莫比乌斯带,下面就来进行演示。
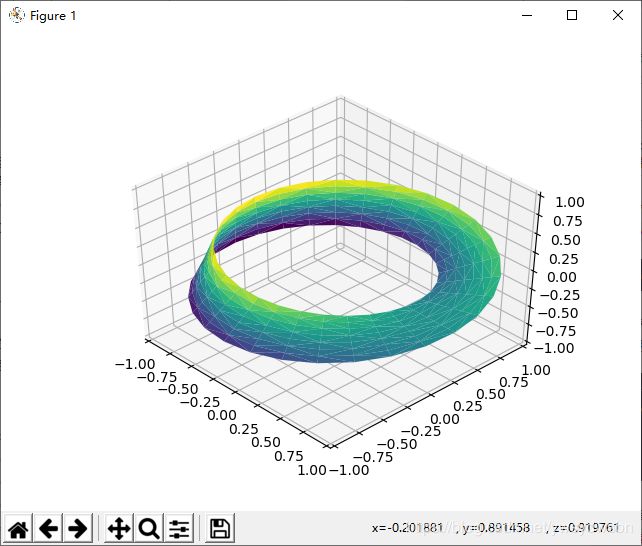
4.3 案例:莫比乌斯带
莫比乌斯带是把一根纸条扭转 180 度后,再把两头粘起来做成的纸带圈。从拓扑学的角度看,莫比乌斯带非常神奇,因为它总共只有一个面!下面我们就用 Matplotlib 的三维工具来画一条莫比乌斯带。此时的关键是想出它的绘图参数:由于它是一条二维带,因此需要两个内在维度(intrinsic dimensions)。让我们把一个维度定义为 θ,取值范围为 0~2 π ;另一个维度是 w,取值范围是 -1~1,表示莫比乌斯带的宽度:
theta = np.linspace(0, 2 * np.pi, 30)
w = np.linspace(-0.25, 0.25, 8)
w, theta = np.meshgrid(w, theta)
有了参数之后,我们必须确定带上每个点的直角坐标 ( x, y, z )。
仔细思考一下,我们可能会找到两种旋转关系:一种是圆圈绕着圆心旋转(角度用 θ 定义),另一种是莫比乌斯带在自己的坐标轴上旋转(角度用 Φ 定义)。因此,对于一条莫比乌斯带,我们必然会有环的一半扭转 180 度,即 Δ Φ = Δ θ / 2。
phi = 0.5 * theta
现在用我们的三角学知识将极坐标转换成三维直角坐标。定义每个点到中心的距离(半径)r,那么直角坐标 ( x, y, z ) 就是:
# x - y平面内的半径
r = 1 + w * np.cos(phi)
x = np.ravel(r * np.cos(theta))
y = np.ravel(r * np.sin(theta))
z = np.ravel(w * np.sin(phi))
最后,要画出莫比乌斯带,还必须确保三角剖分是正确的。最好的实现方法就是首先用基本参数化方法定义三角剖分,然后用 Matplotlib 将这个三角剖分映射到莫比乌斯带的三维空间里,这样就可以画出图形
# 用基本参数化方法定义三角剖分
from matplotlib.tri import Triangulation
tri = Triangulation(np.ravel(w), np.ravel(theta))
ax = plt.axes(projection='3d')
ax.plot_trisurf(x, y, z, triangles=tri.triangles,
cmap='viridis', linewidths=0.2);
ax.set_xlim(-1, 1); ax.set_ylim(-1, 1); ax.set_zlim(-1, 1);
from mpl_toolkits import mplot3d
import numpy as np
import matplotlib.pyplot as plt
theta = np.linspace(0, 2 * np.pi, 30)
w = np.linspace(-0.25, 0.25, 8)
w, theta = np.meshgrid(w, theta)
phi = 0.5 * theta
# x - y平面内的半径
r = 1 + w * np.cos(phi)
x = np.ravel(r * np.cos(theta))
y = np.ravel(r * np.sin(theta))
z = np.ravel(w * np.sin(phi))
# 用基本参数化方法定义三角剖分
from matplotlib.tri import Triangulation
tri = Triangulation(np.ravel(w), np.ravel(theta))
ax = plt.axes(projection='3d')
ax.plot_trisurf(x, y, z, triangles=tri.triangles,cmap='viridis', linewidths=0.2);
ax.set_xlim(-1, 1); ax.set_ylim(-1, 1); ax.set_zlim(-1, 1);
plt.show()
备注
各位老铁来个“关注”、“点赞”、“评论”三连击哦
各位老铁来个“关注”、“点赞”、“评论”三连击哦
各位老铁来个“关注”、“点赞”、“评论”三连击哦