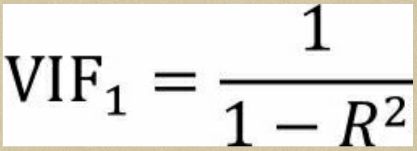第七章线性回归预测模型

前言

线性回归模型属于经典的统计学模型，该模型的应用场景是根据已知的变量（自变量）来预测某个连续的数值变量（因变量）。例如，餐厅根据每天的营业数据（包括菜谱价格、就餐人数、预定人数、特价菜折扣等）预测就餐规模或营业额；网站根据访问的历史数据（包括新用户的注册量、老用户的活跃度、网页内容的更新频率等）预测用户的支付转化率；医院根据患者的病历数据（如体检指标、药物服用情况、平时的饮食习惯等）预测某种疾病发生的概率。
站在数据挖掘的角度看待线性回归模型，它属于一种有监督的学习算法，即在建模过程中必须同时具备自变量x和因变量y。本章的重点就是介绍有关线性回归模型背后的数学原理和应用实战，通过本章内容的学习，读者将会掌握如下内容：

• 一元线性回归模型的实战；
• 多元线性回归模型的系数推导；
• 线性回归模型的假设检验；
• 线性回归模型的诊断；
• 线性回归模型的预测。

7.1　一元线性回归模型

一元线性回归模型也被称为简单线性回归模型，是指模型中只含有一个自变量和一个因变量，用来建模的数据集可以表示成{(x1,y1),(x2,y2),…,(xn,yn)}。其中，xi表示自变量x的第i个值，yi表示因变量y的第i个值，n表示数据集的样本量。当模型构建好之后，就可以根据其他自变量x的值，预测因变量y的值，该模型的数学公式可以表示成：

y=a+bx+ε 

如上公式所示，该模型特别像初中所学的一次函数。其中，a为模型的截距项，b为模型的斜率项，ε为模型的误差项。模型中的a和b统称为回归系数，误差项ε的存在主要是为了平衡等号两边的值，通常被称为模型无法解释的部分。 为了使读者理解简单线性回归模型的数学公式，这里不妨以收入数据集为例，探究工作年限与收入之间的关系。在第6章的数据可视化部分已经介绍了有关散点图的绘制，下面将绘制工作年限与收入的散点图，并根据散点图添加一条拟合线：

# 工作年限与收入之间的散点图
# 导入第三方模块
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
# 导入数据集
income = pd.read_csv(r'D:\projects\notebook\data\Salary_Data.csv')
# 绘制散点图
sns.lmplot(x = 'YearsExperience', y = 'Salary', data = income, ci = None)
# 显示图形
plt.show()

结果:

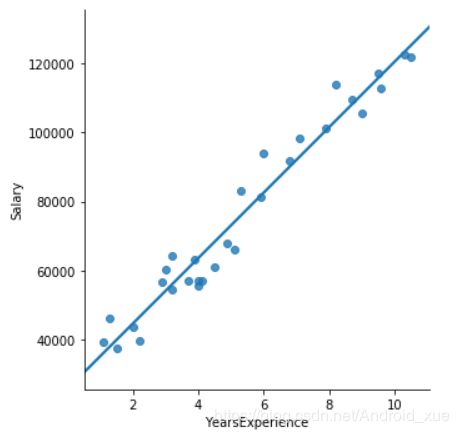
图7-1反映的就是自变量YearsExperience与因变量Salary之间的散点图，从散点图的趋势来看，工作年限与收入之间存在明显的正相关关系，即工作年限越长，收入水平越高。图中的直线就是关于散点的线性回归拟合线，从图中可知，每个散点基本上都是围绕在拟合线附近。虽然通过可视化的方法可以得知散点间的关系和拟合线，但如何得到这条拟合线的数学表达式呢？

拟合线的求解
本节的内容就是关于简单线性回归模型的求解，即如何根据自变量x和因变量y，求解回归系数a和b。前面已经提到，误差项ε是为了平衡等号两边的值，如果拟合线能够精确地捕捉到每一个点（所有的散点全部落在拟合线上），那么对应的误差项ε应该为0。按照这个思路来看，要想得到理想的拟合线，就必须使误差项ε达到最小。由于误差项是y与a+bx的差，结果可能为正值或负值，因此误差项ε达到最小的问题需转换为误差平方和最小的问题（最小二乘法的思路）。误差平方和的公式可以表示为：

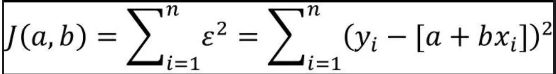
由于建模时的自变量值和因变量值都是已知的，因此求解误差平方和最小值的问题就是求解函数J(a,b)的最小值，而该函数的参数就是回归系数a和b。
该目标函数其实就是一个二元二次函数，如需使得目标函数J(a,b)达到最小，可以使用偏导数的方法求解出参数a和b，进而得到目标函数的最小值。关于目标函数的求导过程如下：

第一步：展开平方项

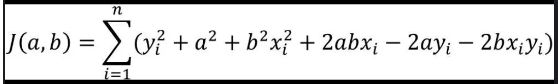
第二步：设偏导数为0

第三步：和公式转换

第四步：化解

第五步：将参数a带入，求解b

如上推导结果所示，参数a和b的值都是关于自变量x和因变量y的公式。接下来，根据该公式，利用Pyhton计算出回归模型的参数值a和b。

# 简单线性回归模型的参数求解
# 样本量
n = income.shape[0]
# 计算自变量、因变量、自变量平方、自变量与因变量乘积的和
sum_x = income.YearsExperience.sum()
sum_y = income.Salary.sum()
sum_x2 = income.YearsExperience.pow(2).sum()
xy = income.YearsExperience * income.Salary
sum_xy = xy.sum()
# 根据公式计算回归模型的参数
b = (sum_xy-sum_x*sum_y/n)/(sum_x2-sum_x**2/n)
a = income.Salary.mean()-b*income.YearsExperience.mean()
# 打印出计算结果
print('回归参数a的值：',a)
print('回归参数b的值：',b)

结果：

回归参数a的值： 25792.200198668666
回归参数b的值： 9449.962321455081

如上所示，利用Python的计算功能，最终得到模型的回归参数值。你可能会觉得麻烦，为了计算回归模型的参数还得人工写代码，是否有现成的第三方模块可以直接调用呢？答案是肯定的，这个模块就是statsmodels，它是专门用于统计建模的第三方模块，如需实现线性回归模型的参数求解，可以调用子模块中的ols函数。有关该函数的语法及参数含义可见下方：

ols(formula, data, subset=None, drop_cols=None)

• formula：以字符串的形式指定线性回归模型的公式，如’y～x’就表示简单线性回归模型。
• data：指定建模的数据集。
• subset：通过bool类型的数组对象，获取data的子集用于建模。
• drop_cols：指定需要从data中删除的变量。

这是一个语法非常简单的函数，而且参数也通俗易懂，但该函数的功能却很强大，不仅可以计算模型的参数，还可以对模型的参数和模型本身做显著性检验、计算模型的决定系数等。接下来，利用该函数计算模型的参数值，进而验证手工方式计算的参数是否正确：

# 导入第三方模块
import statsmodels.api as sm
# 利用收入数据集，构建回归模型
fit = sm.formula.ols('Salary ~ YearsExperience', data = income).fit()
# 返回模型的参数值
fit.params

结果：

Intercept          25792.200199
YearsExperience     9449.962321
dtype: float64

如上结果所示，Intercept表示截距项对应的参数值，YearsExperience表示自变量工作年限对应的参数值。对比发现，函数计算出来的参数值与手工计算的结果完全一致，所以，关于收入的简单线性回归模型可以表示成：

Salary=25792.20+9449.96YearsExperience

7.2　多元线性回归模型

读者会不会觉得一元线性回归模型比较简单呢？它反映的是单个自变量对因变量的影响，然而实际情况中，影响因变量的自变量往往不止一个，从而需要将一元线性回归模型扩展到多元线性回归模型。
如果构建多元线性回归模型的数据集包含n个观测、p+1个变量（其中p个自变量和1个因变量），则这些数据可以写成下方的矩阵形式：

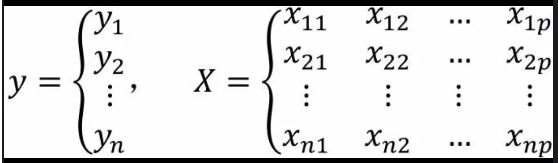
其中，xij代表第个i行的第j个变量值。如果按照一元线性回归模型的逻辑，那么多元线性回归模型应该就是因变量y与自变量X的线性组合，即可以将多元线性回归模型表示成：

y=β0+β1x1+β2x2+…+βpxn+ε

根据线性代数的知识，可以将上式表示成y=Xβ+ε。其中，β为p×1的一维向量，代表了多元线性回归模型的偏回归系数；ε为n×1的一维向量，代表了模型拟合后每一个样本的误差项。

7.2.1　回归模型的参数求解
在多元线性回归模型所涉及的数据中，因变量y是一维向量，而自变量X为二维矩阵，所以对于参数的求解不像一元线性回归模型那样简单，但求解的思路是完全一致的。为了使读者掌握多元线性回归模型参数的求解过程，这里把详细的推导步骤罗列到下方：

第一步：构建目标函数

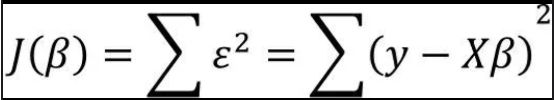
根据线性代数的知识，可以将向量的平方和公式转换为向量的内积，接下来需要对该式进行平方项的展现。

第二步：展开平方项

J(β)=(y-Xβ)'(y-Xβ) 
     =(y'-β'X')(y-Xβ) 
     =(y'y-y'Xβ-β'X'y+β'X'Xβ)

由于上式中的y’Xβ和β’X’y均为常数，并且常数的转置就是其本身，因此y’Xβ和β’X’y是相等的。接下来，对目标函数求参数β的偏导数。

第三步：求偏导

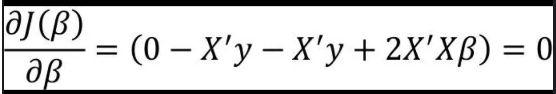
如上式所示，根据高等数学的知识可知，欲求目标函数的极值，一般都需要对目标函数求导数，再令导函数为0，进而根据等式求得导函数中的参数值。

第四步：计算偏回归系数的值

X'Xβ=X'y 
β=(X'X)-1X'y

经过如上四步的推导，最终可以得到偏回归系数β与自变量X、因变量y的数学关系。这个求解过程也被成为“最小二乘法”。基于已知的偏回归系数β就可以构造多元线性回归模型。前文也提到，构建模型的最终目的是为了预测，即根据其他已知的自变量X的值预测未知的因变量y的值。

7.2.2　回归模型的预测
如果已经得知某个多元线性回归模型y=β0+β1x1+β2x2+…+βpxn，当有其他新的自变量值时，就可以将这些值带入如上的公式中，最终得到未知的y值。在Python中，实现线性回归模型的预测可以使用predict“方法”，关于该“方法”的参数含义如下：

predict(exog=None, transform=True)

• exog：指定用于预测的其他自变量的值。
• transform：bool类型参数，预测时是否将原始数据按照模型表达式进行转换，默认为True。

接下来将基于statsmodels模块对多元线性回归模型的参数进行求解，进而依据其他新的自变量值实现模型的预测功能。这里不妨以某产品的利润数据集为例，该数据集包含5个变量，分别是产品的研发成本、管理成本、市场营销成本、销售市场和销售利润，数据集的部分截图如表7-1所示。

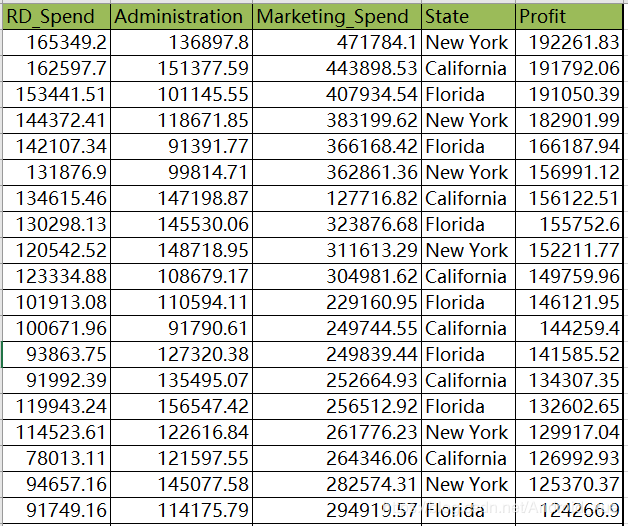
表7-1中数据集中的Profit变量为因变量，其他变量将作为模型的自变量。需要注意的是，数据集中的State变量为字符型的离散变量，是无法直接带入模型进行计算的，所以建模时需要对该变量进行特殊处理。有关产品利润的建模和预测过程如下代码所示：

# 多元线性回归模型的构建和预测
# 导入模块
from sklearn import model_selection
# 导入数据
Profit = pd.read_excel(r'D:\projects\notebook\data\Predict to Profit.xlsx')
# 将数据集拆分为训练集和测试集
train, test = model_selection.train_test_split(Profit, test_size = 0.2, random_state=1234)
# 根据train数据集建模
model = sm.formula.ols('Profit ~ RD_Spend + Administration + Marketing_Spend + C(State)', data = train).fit()
print('模型的偏回归系数分别为：\n', model.params)
# 删除test数据集中的Profit变量，用剩下的自变量进行预测
test_X = test.drop(labels = 'Profit', axis = 1)
pred = model.predict(exog = test_X)
print('对比预测值和实际值的差异：\n',pd.DataFrame({'Prediction':pred,'Real':test.Profit}))

结果：

模型的偏回归系数分别为：
 Intercept               58581.516503
C(State)[T.Florida]       927.394424
C(State)[T.New York]     -513.468310
RD_Spend                    0.803487
Administration             -0.057792
Marketing_Spend             0.013779
dtype: float64
对比预测值和实际值的差异：
        Prediction       Real
8   150621.345801  152211.77
48   55513.218079   35673.41
14  150369.022458  132602.65
42   74057.015562   71498.49
29  103413.378282  101004.64
44   67844.850378   65200.33
4   173454.059691  166187.94
31   99580.888894   97483.56
13  128147.138396  134307.35
18  130693.433835  124266.90

如上结果所示，得到多元线性回归模型的回归系数及测试集上的预测值，为了比较，将预测值和测试集中的真实Profit值罗列在一起。针对如上代码需要说明三点：

• 为了建模和预测，将数据集拆分为两部分，分别是训练集（占80%）和测试集（占20%），训练集用于建模，测试集用于模型的预测。
• 由于数据集中的State变量为非数值的离散变量，故建模时必须将其设置为哑变量的效果，实现方式很简单，将该变量套在C()中，表示将其当作分类（Category）变量处理。
• 对于predict“方法”来说，输入的自变量X与建模时的自变量X必须保持结构一致，即变量名和变量类型必须都相同，这就是为什么代码中需要将test数据集的Profit变量删除的原因。

对于输出的回归系数结果，读者可能会感到疑惑，为什么字符型变量State对应两个回归系数，而且标注了Florida和New York。那是因为字符型变量State含有三种不同的值，分别是California、Florida和New York，在建模时将该变量当作哑变量处理，所以三种不同的值就会衍生出两个变量，分别是State[Florida]和State[New York]，而另一个变量State[California]就成了对照组。
正如建模中的代码所示，将State变量套在C()中，就表示State变量需要进行哑变量处理。但是这样做会存在一个缺陷，那就是无法指定变量中的某个值作为对照组，正如模型结果中默认将State变量的California值作为对照组（因为该值在三个值中的字母顺序是第一个）。如需解决这个缺陷，就要通过pandas模块中的get_dummies函数生成哑变量，然后将所需的对照组对应的哑变量删除即可。为了使读者明白该解决方案，这里不妨重新建模，并以State变量中的New York值作为对照组，代码如下：

# 生成由State变量衍生的哑变量
dummies = pd.get_dummies(Profit.State)
# 将哑变量与原始数据集水平合并
Profit_New = pd.concat([Profit,dummies], axis = 1)
# 删除State变量和California变量（因为State变量已被分解为哑变量，New York变量需要作为参照组）
Profit_New.drop(labels = ['State','New York'], axis = 1, inplace = True)

# 拆分数据集Profit_New
train, test = model_selection.train_test_split(Profit_New, test_size = 0.2, random_state=1234)
# 建模
model2 = sm.formula.ols('Profit ~ RD_Spend + Administration + Marketing_Spend + Florida + California', data = train).fit()
print('模型的偏回归系数分别为：\n', model2.params)

结果：

模型的偏回归系数分别为：
 Intercept          58068.048193
RD_Spend               0.803487
Administration        -0.057792
Marketing_Spend        0.013779
Florida             1440.862734
California           513.468310
dtype: float64

如上结果所示，从离散变量State中衍生出来的哑变量在回归系数的结果里只保留了Florida和California，而New York变量则作为了参照组。以该模型结果为例，得到的模型公式可以表达为：

Profit=58068.05+0.80RD_Spend-0.06Administation+0.01Marketing_Spend+1440.86Florida+513.47California

虽然模型的回归系数求解出来了，但从统计学的角度该如何解释模型中的每个回归系数呢？下面分别以研发成本RD_Spend变量和哑变量Florida为例，解释这两个变量对模型的作用：在其他变量不变的情况下，研发成本每增加1美元，利润会增加0.80美元；在其他变量不变的情况下，以New York为基准线，如果在Florida销售产品，利润会增加1440.86美元。
关于产品利润的多元线性回归模型已经构建完成，但是该模型的好与坏并没有相应的结论，还需要进行模型的显著性检验和回归系数的显著性检验。在下一节，将重点介绍有关线性回归模型中的几点重要假设检验。

7.3　回归模型的假设检验

模型的显著性检验是指构成因变量的线性组合是否有效，即整个模型中是否至少存在一个自变量能够真正影响到因变量的波动。该检验是用来衡量模型的整体效应。回归系数的显著性检验是为了说明单个自变量在模型中是否有效，即自变量对因变量是否具有重要意义。这种检验则是出于对单个变量的肯定与否。
模型的显著性检验和回归系数的显著性检验分别使用统计学中的F检验法和t检验法，接下来将介绍有关F检验和t检验的理论知识和实践操作。

7.3.1　模型的显著性检验——F检验
在统计学中，有关假设检验的问题，都有一套成熟的步骤。首先来看一下如何应用F检验法完成模型的显著性检验，具体的检验步骤如下：
（1）提出问题的原假设和备择假设。
（2）在原假设的条件下，构造统计量F。
（3）根据样本信息，计算统计量的值。
（4）对比统计量的值和理论F分布的值，如果计算的统计量值超过理论的值，则拒绝原假设，否则需接受原假设。

下面将按照上述四个步骤对构造的多元线性回归模型进行F检验，进一步确定该模型是否可用，详细操作步骤如下：
步骤一：提出假设

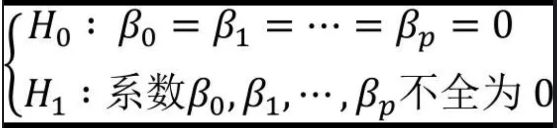
H0为原假设，该假设认为模型的所有偏回归系数全为0，即认为没有一个自变量可以构成因变量的线性组合； H1为备择假设，正好是原假设的对立面，即p个自变量中，至少有一个变量可以构成因变量的线性组合。就F检验而言，研究者往往是更加希望通过数据来推翻原假设H0，而接受备择假设H1的结论。

步骤二：构造统计量
为了使读者理解F统计量的构造过程，可以先观看图7-2，然后掌握总的离差平方和、回归离差平方和与误差平方和的概念与差异。

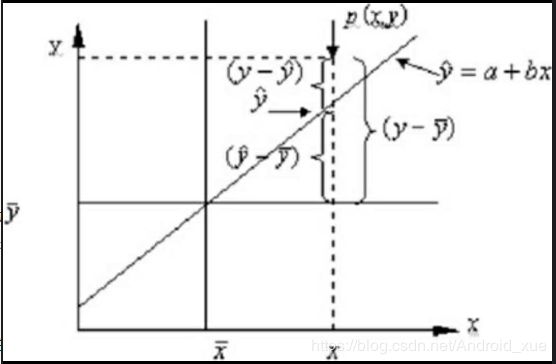
假设图中的斜线代表某条线性拟合线，点p(x,y)代表数据集中的某个点，则为点x处的预测值；为真实值与预测值之间的差异；为预测值与总体平均值之间的差异；为真实值与总体平均值之间的差异。如果将这些差异向量做平方和的计算，则会得到：

如上公式所示，公式中的ESS称为误差平方和，衡量的是因变量的实际值与预测值之间的离差平方和，会随着模型的变化而变动（因为模型的变化会导致预测值的变动）；RSS为回归离差平方和，衡量的是因变量的预测值与实际均值之间的离差平方和，同样会随着模型的变化而变动；TSS为总的离差平方和，衡量的是因变量的值与其均值之间的离差平方和，而其值并不会随模型的变化而变动，即它是一个固定值。
根据统计计算，这三个离差平方和之间存在这样的等式关系：TSS=ESS+RSS。由于TSS的值不会随模型的变化而变动，因此ESS与RSS之间存在严格的负向关系，即ESS的降低会导致RSS的增加。正如7.1.1节所介绍的内容，线性回归模型的参数求解是依据误差平方和最小的理论，如果根据线性回归模型得到的ESS值达到最小，那么对应的RSS值就会达到最大，进而RSS与ESS的商也会达到最大。
按照这个逻辑，便可以构造F统计量，该统计量可以表示成回归离差平方和RSS与误差平方和ESS的公式：

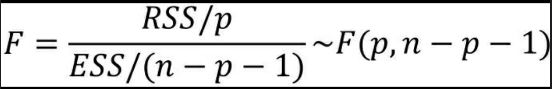
其中，p和n-p-1分别为RSS和ESS的自由度。模型拟合得越好， ESS就会越小， RSS则会越大，得到的F统计量也就越大。
步骤三：计算统计量
下面按照F统计量的公式，运用Python计算该统计量的值，详细的计算过程可见下方代码：

# 导入第三方模块
import numpy as np
# 计算建模数据中，因变量的均值
ybar = train.Profit.mean()
# 统计变量个数和观测个数
p = model2.df_model
n = train.shape[0]
# 计算回归离差平方和
RSS = np.sum((model2.fittedvalues-ybar) ** 2)
# 计算误差平方和
ESS = np.sum(model2.resid ** 2)
# 计算F统计量的值
F = (RSS/p)/(ESS/(n-p-1))
print('F统计量的值：',F)

结果:

F统计量的值： 174.63721716844674

为了验证手工计算的结果是否正确，可以通过fvalue“方法”直接获得模型的F统计量值，如下结果所示，经过对比发现，手工计算的结果与模型自带的F统计量值完全一致：

model2.fvalue

结果：

174.63721715703542

步骤四：对比结果下结论
最后一步所要做的是对比F统计量的值与理论F分布的值，如果读者手中有F分布表，可以根据置信水平（0.05）和自由度（5,34）查看对应的分布值。为了简单起见，这里直接调用Python函数计算理论分布值：

# 导入模块
from scipy.stats import f
# 计算F分布的理论值
F_Theroy = f.ppf(q=0.95, dfn = p,dfd = n-p-1)
print('F分布的理论值为：',F_Theroy)

结果：

F分布的理论值为： 2.502635007415366

如上结果所示，在原假设的前提下，计算出来的F统计量值174.64远远大于F分布的理论值2.50，所以应当拒绝原假设，即认为多元线性回归模型是显著的，也就是说回归模型的偏回归系数都不全为0。

7.3.2　回归系数的显著性检验——t检验
模型通过了显著性检验，只能说明关于因变量的线性组合是合理的，但并不能说明每个自变量对因变量都具有显著意义，所以还需要对模型的回归系数做显著性检验。关于系数的显著性检验，需要使用t检验法，构造t统计量。接下来按照模型显著性检验的四个步骤，对偏回归系数进行显著性检验。
步骤一：提出假设

如前文所提，t检验的出发点就是验证每一个自变量是否能够成为影响因变量的重要因素。t检验的原假设是假定第j变量的偏回归系数为0，即认为该变量不是因变量的影响因素；而备择假设则是相反的假定，认为第j变量是影响因变量的重要因素。

步骤二：构造统计量

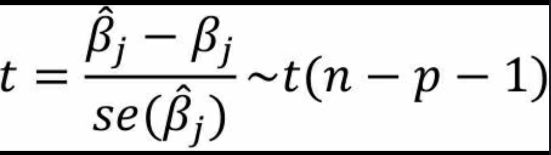
其中，为线性回归模型的第j个系数估计值；βj为原假设中的假定值，即0；为回归系数的标准误，对应的计算公式如下：

其中，为误差平方和，cjj为矩阵(X’X)-1主对角线上第j个元素。

步骤三：计算统计量
如果读者对t统计量值的计算比较感兴趣，可以使用如上公式完成统计量的计算，这里就不手工计算了。为了方便起见，可以直接调用summary“方法”，输出线性回归模型的各项指标值：

# 模型的概览信息
model2.summary()

结果：

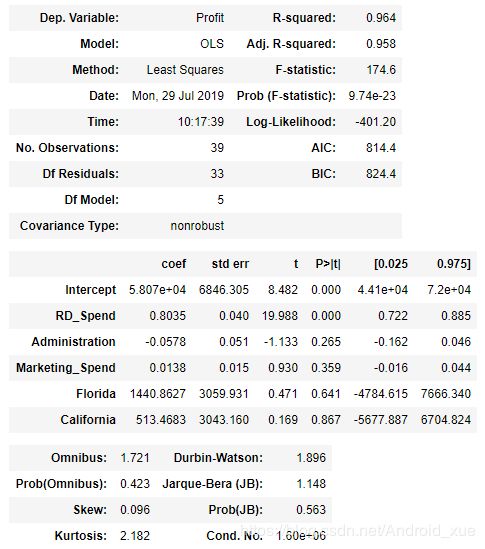
如上结果所示，模型的概览信息包含三个部分，第一部分主要是有关模型的信息，例如模型的判决系数R2，用来衡量自变量对因变量的解释程度、模型的F统计量值，用来检验模型的显著性、模型的信息准则AIC或BIC，用来对比模型拟合效果的好坏等；第二部分主要包含偏回归系数的信息，例如回归系数的估计值Coef、t统计量值、回归系数的置信区间等；第三部分主要涉及模型误差项ε的有关信息，例如用于检验误差项独立性的杜宾－瓦特森统计量Durbin-Watson、用于衡量误差项是否服从正态分布的JB统计量以及有关误差项偏度Skew和峰度Kurtosis的计算值等。

步骤四：对比结果下结论
在第二部分的内容中，含有每个偏回归系数的t统计量值，它的计算就是由估计值coef和标准误std err的商所得的。同时，每个t统计量值都对应了概率值p，用来判别统计量是否显著的直接办法，通常概率值p小于0.05时表示拒绝原假设。从返回的结果可知，只有截距项Intercept和研发成本RD_Spend对应的p值小于0.05，才说明其余变量都没有通过系数的显著性检验，即在模型中这些变量不是影响利润的重要因素。

7.4　回归模型的诊断

当回归模型构建好之后，并不意味着建模过程的结束，还需要进一步对模型进行诊断，目的就是使诊断后的模型更加健壮。统计学家在发明线性回归模型的时候就提出了一些假设前提，只有在满足这些假设前提的情况下，所得的模型才是合理的。本节的主要内容就是针对如下几点假设，完成模型的诊断工作：

• 误差项ε服从正态分布。
• 无多重共线性。
• 线性相关性。
• 误差项ε的独立性。
• 方差齐性。

除了上面提到的五点假设之外，还需要注意的是，线性回归模型对异常值是非常敏感的，即模型的构建过程非常容易受到异常值的影响，所以诊断过程中还需要对原始数据的观测进行异常点识别和处理。接下来，结合理论知识与Python代码逐一展开模型的诊断过程。

7.4.1　正态性检验
虽然模型的前提假设是对残差项要求服从正态分布，但是其实质就是要求因变量服从正态分布。对于多元线性回归模型y=Xβ+ε来说，等式右边的自变量属于已知变量，而等式左边的因变量为未知变量（故需要通过建模进行预测）。所以，要求误差项服从正态分布，就是要求因变量服从正态分布，关于正态性检验通常运用两类方法，分别是定性的图形法（直方图、PP图或QQ图）和定量的非参数法（Shapiro检验和K-S检验），接下来通过具体的代码对原数据集中的利润变量进行正态性检验。

1．直方图法

# 正态性检验
# 直方图法
# 导入第三方模块
import scipy.stats as stats
# 中文和负号的正常显示
plt.rcParams['font.sans-serif'] = ['SimHei']  # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False  # 用来正常显示负号
# 绘制直方图
sns.distplot(a = Profit_New.Profit, bins = 10, fit = stats.norm, norm_hist = True,
             hist_kws = {'color':'steelblue', 'edgecolor':'black'}, 
             kde_kws = {'color':'black', 'linestyle':'--', 'label':'核密度曲线'}, 
             fit_kws = {'color':'red', 'linestyle':':', 'label':'正态密度曲线'})
# 显示图例
plt.legend()
# 显示图形
plt.show()

结果：

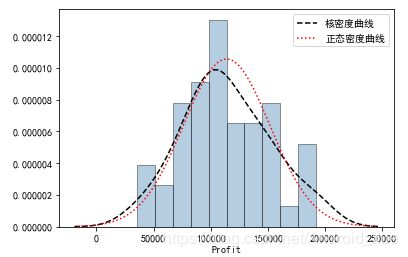
图7-4中绘制了因变量Profit的直方图、核密度曲线和理论正态分布的密度曲线，添加两条曲线的目的就是比对数据的实际分布与理论分布之间的差异。如果两条曲线近似或吻合，就说明该变量近似服从正态分布。从图中看，核密度曲线与正态密度曲线的趋势比较吻合，故直观上可以认为利润变量服从正态分布。

2．PP图与QQ图

# 残差的正态性检验（PP图和QQ图法）
pp_qq_plot = sm.ProbPlot(Profit_New.Profit)
# 绘制PP图
pp_qq_plot.ppplot(line = '45')
plt.title('P-P图')
# 绘制QQ图
pp_qq_plot.qqplot(line = 'q')
plt.title('Q-Q图')
# 显示图形
plt.show()

结果：

PP图的思想是比对正态分布的累计概率值和实际分布的累计概率值，而QQ图则比对正态分布的分位数和实际分布的分位数。判断变量是否近似服从正态分布的标准是：如果散点都比较均匀地散落在直线上，就说明变量近似服从正态分布，否则就认为数据不服从正态分布。从图7-5可知，不管是PP图还是QQ图，绘制的散点均落在直线的附近，没有较大的偏离，故认为利润变量近似服从正态分布。

3．Shapiro检验和K-S检验
这两种检验方法均属于非参数方法，它们的原假设被设定为变量服从正态分布，两者的最大区别在于适用的数据量不一样，若数据量低于5000，则使用shapiro检验法比较合理，否则使用K-S检验法。scipy的子模块stats提供了专门的检验函数，分别是shapiro函数和kstest函数，由于利润数据集的样本量小于5000，故下面运用shapiro函数对利润做定量的正态性检验：

# 导入模块
import scipy.stats as stats
stats.shapiro(Profit_New.Profit)

结果：

(0.9793398380279541, 0.537902295589447)

如上结果所示，元组中的第一个元素是shapiro检验的统计量值，第二个元素是对应的概率值p。由于p值大于置信水平0.05，故接受利润变量服从正态分布的原假设。
为了应用K-S检验的函数kstest，这里随机生成正态分布变量x1和均匀分布变量x2，具体操作代码如下：

# 生成正态分布和均匀分布随机数
rnorm = np.random.normal(loc = 5, scale=2, size = 10000)
runif = np.random.uniform(low = 1, high = 100, size = 10000)
# 正态性检验
KS_Test1 = stats.kstest(rvs = rnorm, args = (rnorm.mean(), rnorm.std()), cdf = 'norm')
KS_Test2 = stats.kstest(rvs = runif, args = (runif.mean(), runif.std()), cdf = 'norm')
print(KS_Test1)
print(KS_Test2)

结果：

KstestResult(statistic=0.0054919289086649, pvalue=0.9236250840080669)
KstestResult(statistic=0.05906629005008068, pvalue=9.941845404073026e-31)

如上结果所示，正态分布随机数的检验p值大于置信水平0.05，则需接受原假设；均匀分布随机数的检验p值远远小于0.05，则需拒绝原假设。需要说明的是，如果使用kstest函数对变量进行正态性检验，必须指定args参数，它用于传递被检验变量的均值和标准差。 如果因变量的检验结果不满足正态分布时，需要对因变量做某种数学转换，使用比较多的转换方法有:

7.4.2　多重共线性检验
多重共线性是指模型中的自变量之间存在较高的线性相关关系，它的存在会给模型带来严重的后果，例如由“最小二乘法”得到的偏回归系数无效、增大偏回归系数的方差、模型缺乏稳定性等，所以，对模型的多重共线性检验就显得尤其重要了。

关于多重共线性的检验可以使用方差膨胀因子VIF来鉴定，如果VIF大于10，则说明变量间存在多重共线性；如果VIF大于100，则表名变量间存在严重的多重共线性。方差膨胀因子VIF的计算步骤如下：
（1）构造每一个自变量与其余自变量的线性回归模型，例如，数据集中含有p个自变量，则第一个自变量与其余自变量的线性组合可以表示为：

x1=c0+α2x1+…+αpxp+ε 

（2）根据如上线性回归模型得到相应的判决系数R2，进而计算第一个自变量的方差膨胀因子VIF：

Python中的statsmodels模块提供了计算方差膨胀因子VIF的函数，下面利用该函数计算两个自变量的方差膨胀因子：

# 导入statsmodels模块中的函数
from statsmodels.stats.outliers_influence import variance_inflation_factor
# 自变量X(包含RD_Spend、Marketing_Spend和常数列1)
X = sm.add_constant(Profit_New.ix[:,['RD_Spend','Marketing_Spend']])

# 构造空的数据框，用于存储VIF值
vif = pd.DataFrame()
vif["features"] = X.columns
vif["VIF Factor"] = [variance_inflation_factor(X.values, i) for i in range(X.shape[1])]
# 返回VIF值
vif

结果：

如上结果所示，两个自变量对应的方差膨胀因子均低于10，说明构建模型的数据并不存在多重共线性。如果发现变量之间存在多重共线性的话，可以考虑删除变量或者重新选择模型（如岭回归模型或LASSO模型）。

7.4.3　线性相关性检验
线性相关性检验，顾名思义，就是确保用于建模的自变量和因变量之间存在线性关系。关于线性关系的判断，可以使用Pearson相关系数和可视化方法进行识别，有关Pearson相关系数的计算公式如下：

其中，COV(x,y)为自变量x与因变量y之间的协方差，D(x)和D(y)分别为自变量x和因变量y的方差。
Pearson相关系数的计算可以直接使用数据框的corrwith“方法”，该方法最大的好处是可以计算任意指定变量间的相关系数。下面使用该方法计算因变量与每个自变量之间的相关系数，具体代码如下：

# 计算数据集Profit_New中每个自变量与因变量利润之间的相关系数
Profit_New.drop('Profit', axis = 1).corrwith(Profit_New.Profit)

结果：

RD_Spend           0.978437
Administration     0.205841
Marketing_Spend    0.739307
California        -0.083258
Florida            0.088008
dtype: float64

如上结果所示，自变量中只有研发成本和市场营销成本与利润之间存在较高的相关系数，相关性分别达到0.978和0.739，而其他变量与利润之间几乎没有线性相关性可言。通常情况下，可以参考表7-3判断相关系数对应的相关程度：

以管理成本Administration为例，与利润之间的相关系数只有0.2，被认定为不相关，这里的不相关只能说明两者之间不存在线性关系。如果利润和管理成本之间存在非线性关系时，Pearson相关系数也同样会很小，所以还需要通过可视化的方法，观察自变量与因变量之间的散点关系。
读者可以应用matplotlib模块中的scatter函数绘制五个自变量与因变量之间的散点图，那样做可能会使代码显得冗长。这里介绍另一个绘制散点图的函数，那就是seaborn模块中的pairplot函数，它可以绘制多个变量间的散点图矩阵。

# 散点图矩阵
# 导入模块
import matplotlib.pyplot as plt
import seaborn
# 绘制散点图矩阵
seaborn.pairplot(Profit_New.ix[:,['RD_Spend','Administration','Marketing_Spend','Profit']])
# 显示图形
plt.show()

结果：

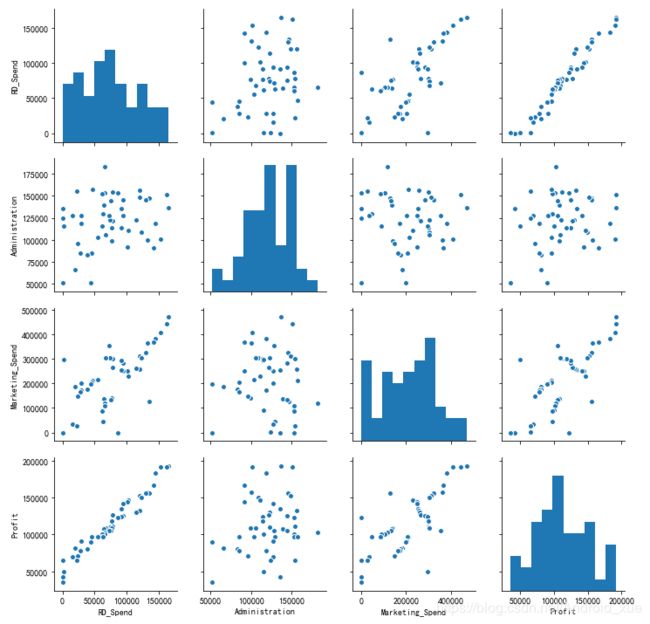
如图7-6所示，由于California与Florida都是哑变量，故没有将其放入散点图矩阵中。从图中结果可知，研发成本与利润之间的散点图几乎为一条向上倾斜的直线（见左下角的散点图），说明两种变量确实存在很强的线性关系；市场营销成本与利润的散点图同样向上倾斜，但很多点的分布还是比较分散的（见第一列第三行的散点图）；管理成本与利润之间的散点图呈水平趋势，而且分布也比较宽，说明两者之间确实没有任何关系（见第一列第二行的散点图）。
以7.2.2节中重构的模型model2为例，综合考虑相关系数、散点图矩阵和t检验的结果，最终确定只保留模型model2中的RD_Spend和Marketing_Spend两个自变量，下面重新对该模型做修正：

# 模型修正
model3 = sm.formula.ols('Profit ~ RD_Spend + Marketing_Spend', data = train).fit()
# 模型回归系数的估计值
model3.params

结果：

Intercept          51902.112471
RD_Spend               0.785116
Marketing_Spend        0.019402
dtype: float64

如上结果所示，返回的是模型两个自变量的系数估计值，可以将多元线性回归模型表示成：

Profit=51902.11+0.79RD_Spend+0.02Marketing_Spend

7.4.4　异常值检验

由于多元线性回归模型容易受到极端值的影响，故需要利用统计方法对观测样本进行异常点检测。如果在建模过程中发现异常数据，需要对数据集进行整改，如删除异常值或衍生出是否为异常值的哑变量。对于线性回归模型来说，通常利用帽子矩阵、DFFITS准则、学生化残差或Cook距离进行异常点检测。接下来，分别对这四种检测方法做简单介绍。

1．帽子矩阵
帽子矩阵的设计思路就是考察第i个样本对预测值:

的影响大小，根据7.2.1节中推导得到的回归系数求解公式，可以将多元线性回归模型表示成：

其中，H=X(X’X)-1X’，H就称为帽子矩阵，全都是关于自变量X的计算。判断样本是否为异常点的方法，可以使用如下公式：

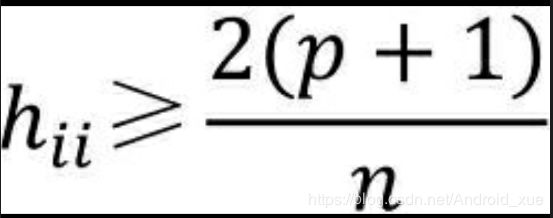
其中，hii为帽子矩阵H的第i个主对角线元素，p为自变量个数，n为用于建模数据集的样本量。如果对角线元素满足上面的公式，则代表第i个样本为异常观测。

2．DFFITS准则
DFFITS准则借助于帽子矩阵，构造了另一个判断异常点的统计量，该统计量可以表示成如下公式：

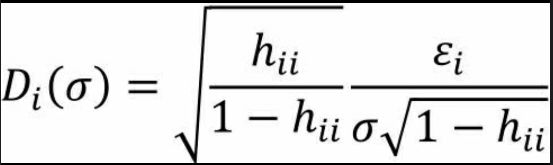
其中，hii为帽子矩阵H的第i个主对角线元素，εi为第i个样本点的预测误差，σ为误差项的标准差，判断样本为异常点的方法，可以使用如下规则：

需要注意的是，在DFFITS准则的公式中，乘积的第二项实际上是学生化残差，也可以用来判定第i个样本是否为异常点，判断标准如下：

3．Cook距离
Cook距离是一种相对抽象的判断准则，无法通过具体的临界值判断样本是否为异常点，对于该距离，Cook统计量越大的点，其成为异常点的可能性越大。Cook统计量可以表示为如下公式：

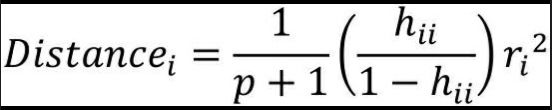
其中，ri为学生化残差。
如果使用如上四种方法判别数据集的第i个样本是否为异常点，前提是已经构造好一个线性回归模型，然后基于get_influence“方法”获得四种统计量的值。为了检验模型中数据集的样本是否存在异常，这里沿用上节中构造的模型model3，具体代码如下：

# 异常值检验
outliers = model3.get_influence()

# 高杠杆值点（帽子矩阵）
leverage = outliers.hat_matrix_diag
# dffits值
dffits = outliers.dffits[0]
# 学生化残差
resid_stu = outliers.resid_studentized_external
# cook距离
cook = outliers.cooks_distance[0]

# 合并各种异常值检验的统计量值
contat1 = pd.concat([pd.Series(leverage, name = 'leverage'),pd.Series(dffits, name = 'dffits'),
                     pd.Series(resid_stu,name = 'resid_stu'),pd.Series(cook, name = 'cook')],axis = 1)
# 重设train数据的行索引
train.index = range(train.shape[0])
# 将上面的统计量与train数据集合并
profit_outliers = pd.concat([train,contat1], axis = 1)
profit_outliers.head()

结果:

如表7-4所示，合并了train数据集和四种统计量的值，接下来要做的就是选择一种或多种判断方法，将异常点查询出来。为了简单起见，这里使用标准化残差，当标准化残差大于2时，即认为对应的数据点为异常值。

# 计算异常值数量的比例
outliers_ratio = sum(np.where((np.abs(profit_outliers.resid_stu)>2),1,0))/profit_outliers.shape[0]
outliers_ratio

结果：

0.02564102564102564

如上结果所示，通过标准化残差监控到了异常值，并且异常比例为2.5%。对于异常值的处理办法，可以使用两种策略，如果异常样本的比例不高（如小于等于5%），可以考虑将异常点删除；如果异常样本的比例比较高，选择删除会丢失一些重要信息，所以需要衍生哑变量，即对于异常点，设置哑变量的值为1，否则为0。如上可知，建模数据的异常比例只有2.5%，故考虑将其删除。

# 挑选出非异常的观测点
none_outliers = profit_outliers.ix[np.abs(profit_outliers.resid_stu)<=2,]

# 应用无异常值的数据集重新建模
model4 = sm.formula.ols('Profit ~ RD_Spend + Marketing_Spend', data = none_outliers).fit()
model4.params

结果：

Intercept          51827.416821
RD_Spend               0.797038
Marketing_Spend        0.017740
dtype: float64

如上结果所示，经过异常点的排除，重构模型的偏回归系数发生了变动，故可以将模型写成如下公式：

Profit=51827.42+0.80RD_Spend+0.02Marketing_Spend

7.4.5　独立性检验
残差的独立性检验，说白了也是对因变量y的独立性检验，因为在线性回归模型的等式左右只有y和残差项ε属于随机变量，如果再加上正态分布，就构成了残差项独立同分布于正态分布的假设。关于残差的独立性检验通常使用Durbin-Watson统计量值来测试，如果DW值在2左右，则表明残差项之间是不相关的；如果与2偏离的较远，则说明不满足残差的独立性假设。对于DW统计量的值，其实都不需要另行计算，因为它包含在模型的概览信息中，以模型model4为例：

# Durbin-Watson统计量
# 模型概览
model4.summary()

结果:

如表7-5所示，残差项对应的DW统计量值为2.065，比较接近于2，故可以认为模型的残差项之间是满足独立性这个假设前提的。

7.4.6　方差齐性检验
方差齐性是要求模型残差项的方差不随自变量的变动而呈现某种趋势，否则，残差的趋势就可以被自变量刻画。如果残差项不满足方差齐性（方差为一个常数），就会导致偏回归系数不具备有效性，甚至导致模型的预测也不准确。所以，建模后需要验证残差项是否满足方差齐性。关于方差齐性的检验，一般可以使用两种方法，即图形法（散点图）和统计检验法（BP检验）。

1．图形法
如上所说，方差齐性是指残差项的方差不随自变量的变动而变动，所以只需要绘制残差与自变量之间的散点图，就可以发现两者之间是否存在某种趋势：

# 方差齐性检验
# 设置第一张子图的位置
ax1 = plt.subplot2grid(shape = (2,1), loc = (0,0))
# 绘制散点图
ax1.scatter(none_outliers.RD_Spend, (model4.resid-model4.resid.mean())/model4.resid.std())
# 添加水平参考线
ax1.hlines(y = 0 ,xmin = none_outliers.RD_Spend.min(),xmax = none_outliers.RD_Spend.max(), color = 'red', linestyles = '--')
# 添加x轴和y轴标签
ax1.set_xlabel('RD_Spend')
ax1.set_ylabel('Std_Residual')

# 设置第二张子图的位置
ax2 = plt.subplot2grid(shape = (2,1), loc = (1,0))
# 绘制散点图
ax2.scatter(none_outliers.Marketing_Spend, (model4.resid-model4.resid.mean())/model4.resid.std())
# 添加水平参考线
ax2.hlines(y = 0 ,xmin = none_outliers.Marketing_Spend.min(),xmax = none_outliers.Marketing_Spend.max(), color = 'red', linestyles = '--')
# 添加x轴和y轴标签
ax2.set_xlabel('Marketing_Spend')
ax2.set_ylabel('Std_Residual')

# 调整子图之间的水平间距和高度间距
plt.subplots_adjust(hspace=0.6, wspace=0.3)
# 显示图形
plt.show()

结果：

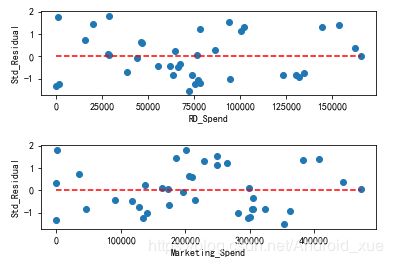
如图7-7所示，标准化残差并没有随自变量的变动而呈现喇叭形，所有的散点几乎均匀地分布在参考线y=0的附近。所以，可以说明模型的残差项满足方差齐性的前提假设。

2．BP检验
方差齐性检验的另一个统计方法是BP检验，它的原假设是残差的方差为一个常数，通过构造拉格朗日乘子LM统计量，实现方差齐性的检验。该检验可以借助于statsmodels模块中的het_breushpagan函数完成，具体代码如下：

# BP检验
sm.stats.diagnostic.het_breushpagan(model4.resid, exog_het = model4.model.exog)

结果：

(1.467510366830809,
 0.48010272699006995,
 0.7029751237162342,
 0.5019659740962923)

如上结果所示，元组中一共包含四个值，第一个值1.468为LM统计量；第二个值是统计量对应的概率p值，该值大于0.05，说明接受残差方差为常数的原假设；第三个值为F统计量，用于检验残差平方项与自变量之间是否独立，如果独立则表明残差方差齐性；第四个值则为F统计量的概率p值，同样大于0.05，则进一步表示残差项满足方差齐性的假设。
如果模型的残差不满足齐性的话，可以考虑两类方法来解决，一类是模型变换法，另一类是“加权最小二乘法”（可以使用statsmodels模块中的wls函数）。对于模型变换法来说，主要考虑残差与自变量之间的关系，如果残差与某个自变量x成正比，则需将原模型的两边同除以；如果残差与某个自变量x的平方成正比，则需将原始模型的两边同除以x；对于加权最小二乘法来说，关键是如何确定权重，根据多方资料的搜索和验证，一般选择如下三种权重来进行对比测试：

• 残差绝对值的倒数作为权重。
• 残差平方的倒数作为权重。
• 用残差的平方对数与自变量X重新拟合建模，并将得到的拟合值取指数，用指数的倒数作为权重。

3．回归模型的预测
经过前文的模型构造、假设检验和模型诊断，最终确定合理的模型model4。接下来要做的就是利用该模型完成测试集上的预测，具体代码如下：

# 模型预测
# model4对测试集的预测
pred4 = model4.predict(exog = test.ix[:,['RD_Spend','Marketing_Spend']])
# 对比预测值与实际值
pd.DataFrame({'Prediction':pred4,'Real':test.Profit})
# 绘制预测值与实际值的散点图
plt.scatter(x = test.Profit, y = pred4)
# 添加斜率为1，截距项为0的参考线
plt.plot([test.Profit.min(),test.Profit.max()],[test.Profit.min(),test.Profit.max()],
        color = 'red', linestyle = '--')
# 添加轴标签
plt.xlabel('实际值')
plt.ylabel('预测值')
# 显示图形
plt.show()

结果：

如图7-8所示，绘制了有关模型在测试集上的预测值和实际值的散点图，该散点图可以用来衡量预测值与实际值之间的距离差异。如果两者非常接近，那么得到的散点图一定会在对角线附近微微波动。从图7-8的结果来看，大部分的散点都落在对角线附近，说明模型的预测效果还是不错的。

7.5　本章小结

本章重点介绍了有关线性回归模型的理论知识与应用实战，内容包含模型回归系数的求解、模型及系数的显著性检验、模型的假设诊断及预测。在实际应用中，如果因变量为数值型变量，可以考虑使用线性回归模型，但是前提得满足几点假设，如因变量服从正态分布、自变量间不存在多重共线性、自变量与因变量之间存在线性关系、用于建模的数据集不存在异常点、残差项满足方差异性和独立性。 为了使读者掌握有关线性回归模型的函数和“方法”，这里将其重新梳理一下，以便读者查阅和记忆：