基于spss的多变量时间序列的ARIMA模型

概述

数学建模的过程中必然会出现许多难以预料的问题，哪怕仅仅是一个温度预测模型也有莫大学问，譬如预测二十四小时内的温度变化，这多变量时间序列短期预测确实让我伤透了脑筋。

查阅了不少资料后，小弟我也勉勉强强总结出一套行之有效的办法，如有错漏，还请各位大佬予以指正。

基本步骤

1、根据时间序列的散点图、自相关函数和偏自相关函数图识别其平稳性。

2、对非平稳的时间序列数据进行平稳化处理。直到处理后的自相关函数和偏自相关函数的数值非显著非零。

3、根据所识别出来的特征建立相应的时间序列模型。平稳化处理后，若偏自相关函数是截尾的，而自相关函数是拖尾的，则建立AR模型；若偏自相关函数是拖尾的，而自相关函数是截尾的，则建立MA模型；若偏自相关函数和自相关函数均是拖尾的，则序列适合ARIMA模型。

链接: ARIMA模型详解.

4、参数估计，检验是否具有统计意义。

5、假设检验，判断（诊断）残差序列是否为白噪声序列。

白噪声在实际拟合模型的时候其实就是残余数，模型加上这个是为了解释只用ARMA部分预测不了的随机性。

6、利用已通过检验的模型进行预测。

引言

要进行多变量时间序列的分析预测，首先对单变量进行建模，并分析判断其在建模过程中表现出来的种种特性，有的童鞋上来直接进行多变量分析，把变量一股脑的扔到这里。

然后直接确定，最后结果只能是……

工欲善其事必先利其器，让我们从单变量开始吧。

链接: 具体步骤请点我.

具体步骤百度经验上有详细的介绍，这里不再赘述，反正大家对网上能搜到的东西也不是很感兴趣。

下面直接把我建模过程中遇到的问题和自认为的中间简略说一下。

单变量时间模型

因为我要完成的是基于大量数据（近100天）的短时间（24小时）预测，故不必分析季节成分。

ARIMA模型要求序列是平稳序列，因此要对数据进行平稳性分析。

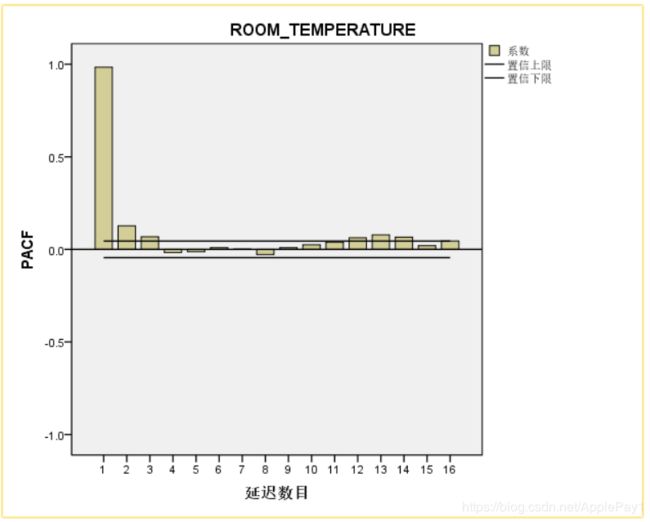
由上述序列的自相关图（ACF）和偏自相关图（PACF）分析可知，其都是拖尾的，说明序列是非平稳的。温度数据序列通常不是平稳序列，但一般一阶差分都是平稳的，因此可以通过差分做进一步分析。

*自相关函数ACF描述的是时间序列观测值与其过去的观测值之间的线性相关性。

*偏自相关函数PACF描述的是在给定中间观测值的条件下，时间序列观测值预期过去的观测值之间的线性相关性。

根据差分序列图，观察其平稳性，差分序列基本均匀分布在0刻度线上下两侧，因此可以认为差分序列是平稳的。

差分闲话：差分，一般在大数据里用在以时间为统计维度的分析中，其实就是下一个数值 ，减去上一个数值 。

差分: 感兴趣的请点这里.

差分序列的ACF和PACF都是拖尾的，因此，可对原始序列建立ARIMA(p,1,q)模型。

链接: 关于截尾和拖尾

经过对图像的分析处理，确定模型为ARIMA(2,1,13)

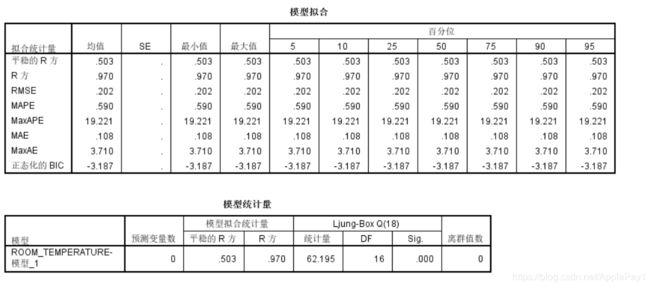
得出的数据：平稳的R方：决定系数，现有模型所能够解释的原变量的多少变异（较客观）。R方：原数据去掉季节趋势，波动趋势，周期趋势之后的变异解释度（偏高）。

RMSE：残差均方。

MAPE：平均相对误差。

MAXApe：最大的相对百分比误差。

MAE：平均实测误差。

MAXAE：最大的绝对误差。

多变量时间模型

之前一直搞不懂缺失数据什么意思，后来发现是要预测未来的时间，必须有对应的时间数据和自变量数据。

在单变量之后，要进行多变量预测，必须先替换缺失值，比如说变量数据到八月二十日，要预测八月二十一日，必须用一定方法替换缺失值。

由于我们刚才已经进行过单变量预测了，其要预测的变量即因变量的预测结果已经在spss中有所体现，所以此时直接替换即可。

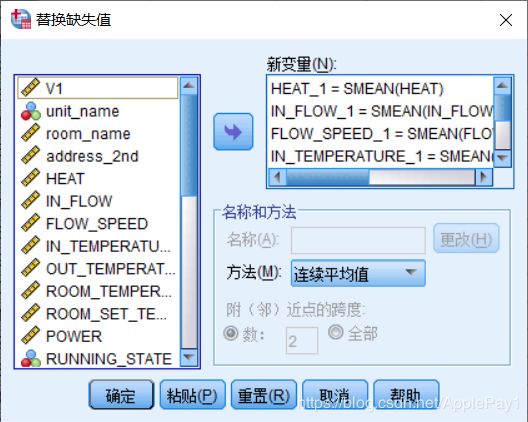
我这里采用的是连续平均值法，把替换后的变量作为新的自变量输入。

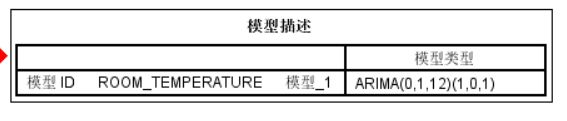
可以如上述的过程进行序列图预测，自相关诊断，判断出是否采用ARIMA模型既确定模型参数，也可以像我一样直接选择‘专家建模器’，用它的内置算法判断模型参数和季节性。

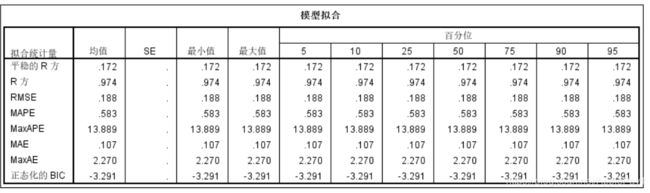
建模结果如下：

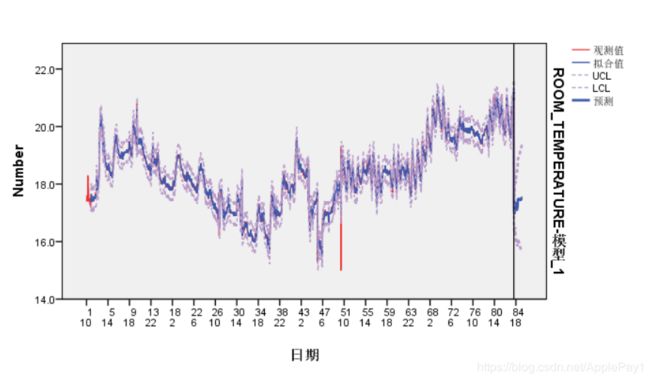
由模型图可以得出，q检验置信水平94%，R的平方达到0.974，拟合程度很好，模型参数sig都小于0.05，即系数显著不为零。

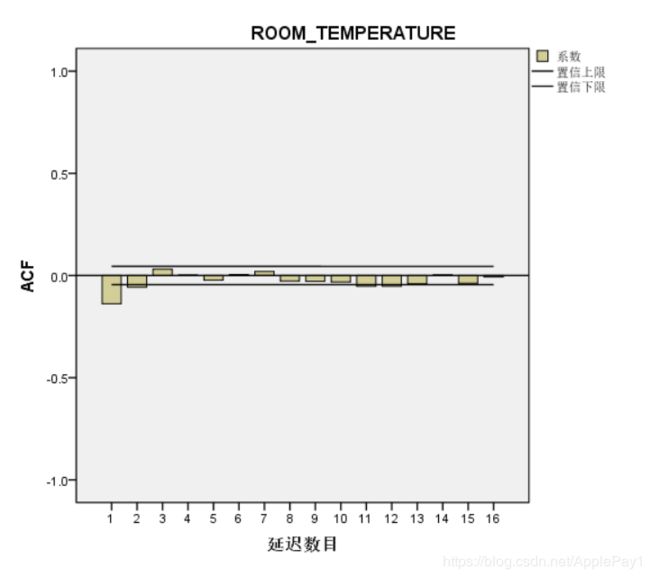
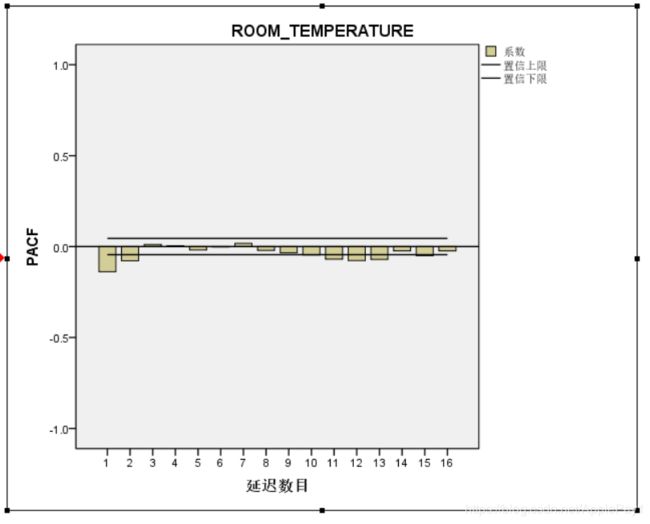
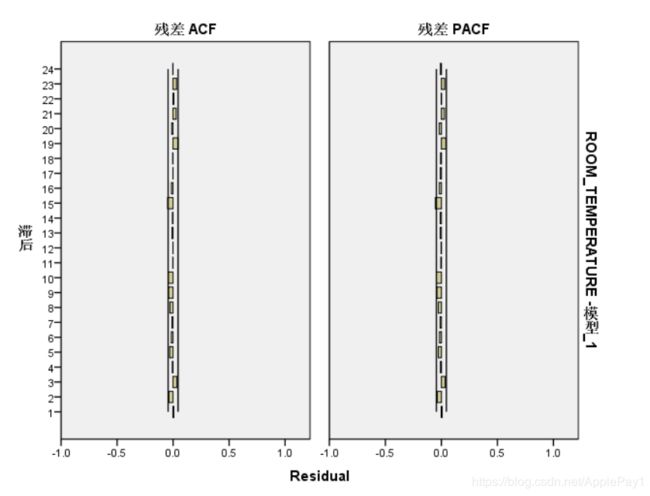
再看残差的ACF和PACF图，可以看到都是平稳的。

最后模型预测温度：T(t)=0.71T(t-1)+0.670ε(t)-0.51F(in_flow)+0.004F(heat)-4.326F(flow_speed)-0.258F(power)-0.75F(out_temperature)。

至此全过程完毕。

感谢各位看官老爷的耐心阅读，不才在此抛砖引玉，文笔拙陋，还请见谅，如果列位在看完之后，偶然能有所体会，有所感悟，我将不甚欣喜。