数据挖掘:模型选择——监督学习(回归)
数据挖掘:模型选择——监督学习(回归)
在上一篇文章数据挖掘:模型选择——监督学习(分类)中介绍了分类相关的算法原理,这次来介绍回归的一些算法。回归主要是预测连续型数据的目标值。
本文来自:机器学习菜菜课堂
一、线性回归
简单介绍:
简答的线性回归如y=ax+b,这是只有一个特征时的情况,而对于多个特征,就变成了多元线性回归。公式如下:
![]()
这个θ为对应自变量的权重值,越大,证明该特征对结果的影响越重要。由此可以对特征进行筛选。而我们要求得就是这个参数。
工作原理:
一般遇到机器学习的问题,首先都是先定义损失函数。通过对损失函数的优化来求解参数。
这里用真实值和预测值的残差平方和作为要优化的损失函数,也就是θ取何值时,能让它最小。最小二乘法

这里有两种方法进行求解,利用矩阵求解,梯度下降法。
利用矩阵求解:


梯度下降法:


主要参数:
没有参数可以调。所以这个模型无法通过调整参数来优化模型,它只依靠数据。另外,LR需要做归一化/标准化。
算法特点:
优点:结果易于理解,计算上不复杂。
缺点:对非线性的数据拟合不好。易过拟合,因为寻求的是最优解。
因为线性回归假设特征和结果之间满足线性关系。
sklearn代码:
from sklearn.linear_model import LinearRegression as LR
reg = LR().fit(Xtrain,Ytrain)
yhat = reg.predict(Xtest)
二、岭回归和Lasso回归
岭回归:
简单介绍:
在多元线性的求解推导中,存在逆矩阵,而如果数据的逆矩阵不存在(数据间存在多重共线性,完全线性相关或高度线性相关)的话,那么模型的预测效果并不会很好。会求出很大的θ造成模型有偏差,或者不可用。
多重共线性可用VIF(方差膨胀因子来衡量)。另外,为了解决线性回归的多重共线性问题,可用岭回归和Lasso回归。
工作原理:
岭回归和Lasso回归都是在线性回归的损失函数上加上正则项。岭回归加的是系数的L2范数,Lasso加的是系数的L1范数。
岭回归:
岭回归的损失函数:
![]()

在加上a后,只要a不为0或与原矩阵的对角线上的不为相反数,可保证矩阵为可逆矩阵。a的值人为设定。
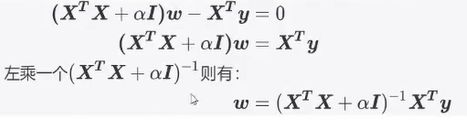

主要参数:
正则化系数a。如a很小,那么对原来的式子不起作用,非有效的ω。如果a很大,那么会使回归系数发生偏移(a削弱了原本ω所代表的信息)。
通过调整alpha的取值,若模型没有明显的改变,则说明数据间没有多重共线性。若有上升的趋势,则说明数据间存在多重共线性。alpha取值通过模型的偏差,方差进行调整。主要通过交叉验证,进行选择。这里用带交叉验证的岭回归。
对损失函数求导。

这时的alpha无法对矩阵是否可逆造成影响。lasso无法解决多重共线性的问题。
但在实际问题中,数据之间既没有完全相关,也没有完全独立的。所以,假设矩阵的逆是一直存在的。

alpha可以限制参数的大小,防止因为多重共线性导致的w被估计过大,导致模型不准确。Lasso不能解决多重共线性,但能限制其影响。alpha压缩了w系数对原本数据的拟合程度,所以lasso可以做特征选择。
L1和L2正则化一个核心差异就是他们对系数 的影响:两个正则化都会压缩系数 的大小,对标签贡献更少的特征的系数会更小,也会更容易被压缩。
不过,L2正则化只会将系数压缩到尽量接近0,但L1正则化主导稀疏性,因此会将系数压缩到0。这个性质,让Lasso成为了线性模型中的特征选择工具首选。
在Lasso上选取alpha值,通过交叉验证。LassoCV.
eps跟n_alphas。eps取的很小。
sklearn代码:
from sklearn.linear_model import Ridge,Lasso
reg = Ridge(alpha=1).fit(Xtrain,Ytrain)
reg = Lasso(alpha=1).fit(Xtrain,Ytrain)
三、多项式回归
线性数据与非线性数据:
线性关系:
”线性“这个词用于描述不同事物时有着不同的含义。我们最常使用的线性是指“变量之间的线性关系(linear relationship)”,它表示两个变量之间的关系可以展示为一条直线,即可以使用方程 来进行拟合。一般通过绘制散点图来看。
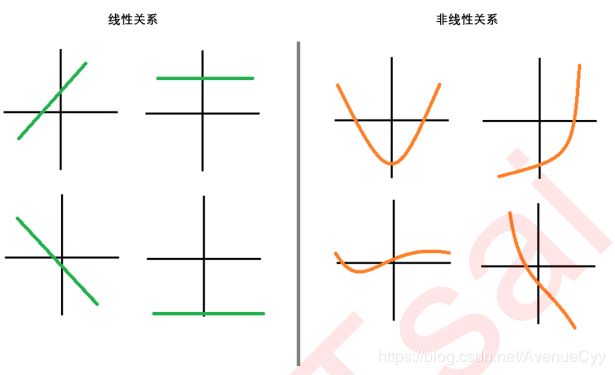
线性数据:
通常来说,一组数据由多个特征和标签组成。当这些特征分别与标签存在线性关系的时候,我们就说这一组数据是线性数据。而任一特征与标签之间的关系需要三角函数,指数等来定义,那么就叫非线性数据。
对于线性和非线性数据,最简单的判别方法就是利用模型来帮助我们——如果是做分类则使用逻辑回归,如果做回归则使用线性回归,如果效果好那数据是线性的,效果不好则数据不是线性的。当然,也可以降维后进行绘图,绘制出的图像分布接近一条直线,则数据就是线性的。
线性关系图,探索的是特征和目标变量的关系。
回归问题:

分类问题
当我们在进行分类的时候,我们的决策函数往往是一个分段函数,比如二分类下的决策函数可以是符号函数 ,符号函数的图像可以表示为取值为1和-1的两条直线。这个函数明显不符合我们所说的可以使用一条直线来进行表示的属性,因此分类问题中特征与标签[0,1]或者[-1,1]之间关系明显是非线性的关系。除非我们在拟合分类的概率,否则不存在例外。
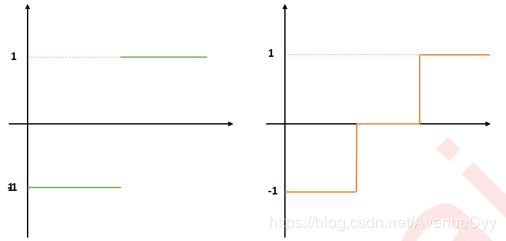
这个是数据分布图,横纵坐标是特征。其中的颜色是目标变量。关心不是拟合,而是能否找到一条直线,将其分开。

总结一下,对于回归问题,数据若能分布为一条直线,则是线性的,否则是非线性。对于分类问题,数据分布若能使用一条直线来划分类别,则是线性可分的,否则数据则是线性不可分的。
线性模型与非线性模型:
我们建立的线性回归模型,是一个用于拟合线性数据的线性模型。
![]()
作为线性模型的典型代表,我们可以从线性回归的方程中总结出线性模型的特点:其自变量都是一次项。
非线性模型拟合线性数据:
线性数据对非线性模型来说比较简单,容易把训练集上的R2训练得很高,MSE训练得很低。效果好,易过拟合。
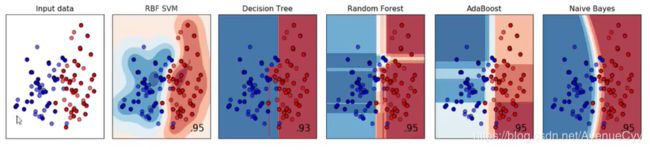
线性模型拟合非线性数据:
单纯的线性模型处理非线性数据不好。可用线性模型处理分箱之后的非线性数据。

线性模型们的决策边界都是一条条平行的直线,而非线性模型们的决策边
界是交互的直线(格子),曲线,环形等等。对于分类模型来说,这是我们判断模型是线性还是非线性的重要评判因素:线性模型的决策边界是平行的直线,非线性模型的决策边界是曲线或者交叉的直线。对分类问题而言,如果一个分类模型的决策边界上自变量的最高次方为1,则我们称这个模型是线性模型。
既是线性,也是非线性的模型
比如SVM,没有核的SVM是线性模型,有核的是非线性模型。
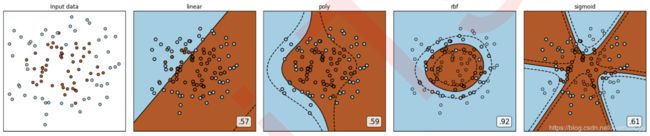
主要在二维空间中看决策边界和拟合图形是不是直线。
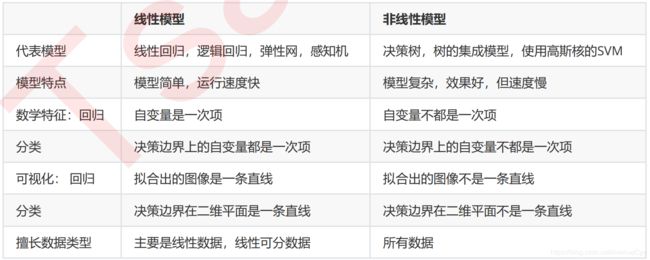
离散化:
利用分箱,离散化连续型变量的方法来处理原始数据,以此来提升线性回归的表现。
from sklearn.preprocessing import KBinsDiscretizer
#将数据分箱
enc = KBinsDiscretizer(n_bins=10 #分几类?
,encode="onehot")

另外,分箱数是能影响拟合效果的。利用交叉验证来选择最优的箱子数。另一种更普遍的处理非线性数据的方法是多项式回归。主要是利用跟SVM一样的升维思想。
多项式回归:
通过增加自变量的次数(多项式变化),来对线性模型达到升维的效果。
多项式变化是对原始数据进行调整,从而使其能被线性模型拟合。
from sklearn.preprocessing import PolynomialFeatures
import numpy as np
X = np.arange(1,4).reshape(-1,1)
poly = PolynomialFeatures(degree=2)
X_ = poly.fit_transform(X)
X_
可得到如下的结果:

这时,再用线性回归来拟合。线性回归是会对每个特征拟合出权重 的,所
以当我们拟合高维数据的时候,我们会得到下面的模型:
![]()
而对计算机来说,不理解什么是截距和系数。因此x0也会被认为是系数。所以,一般不求截距。
以上是针对数据一维的情况,而二维的情况如下:


当我们进行多项式转换的时候,多项式会产出到最高次数为止的所有低高次项。比如如果我们规定多项式的次数为2,多项式就会产出所有次数为1和次数为2的项反馈给我们,相应的如果我们规定多项式的次数为n,则多项式会产出所有从次数为1到次数为n的项。
在多项式回归中,我们可以规定是否产生平方或者立方项,其实如果我们只要求高次项的话, 会是一个比 更好的高次项,因为 x1x2和 x1之间的共线性会比 x1x1与 x1之间的共线性好那么一点点(只是一点点),而我们多项式转化之后是需要使用线性回归模型来进行拟合的,就算机器学习中不是那么在意数据上的基本假设,但是太过分的共线性还是会影响到模型的拟合。因此sklearn中存在着控制是否要生成平方和立方项的参数interaction_only,默认为False,以减少共线性。
多项式回归的方程是由原始数据的维度和我们设定的最高次数决定的。因此,多
项式回归没有固定的模型表达式。
多项式回归处理非线性问题:
from sklearn.preprocessing import PolynomialFeatures as PF
from sklearn.linear_model import LinearRegression
import numpy as np
d=5
#进行高此项转换
poly = PF(degree=d)
X_ = poly.fit_transform(X)
line_ = PF(degree=d).fit_transform(line)
#训练数据的拟合
LinearR_ = LinearRegression().fit(X_, y)
LinearR_.score(X_,y)
多项式回归能够较好地拟合非线性数据,还不容易发生过拟合,可以说是保留了线性回归作为线性模型所带的“不容易过拟合”和**“计算快速**”的性质,同时又实现了优秀地拟合非线性数据.
多项式回归的可解释性:
当我们进行了多项式转换后,尽管我们还是形成形如线性回归的方程,但随着数据维度和多项式次数的上升,方程也变得异常复杂,我们可能无法一眼看出增维后的特征是由之前的什么特征组成的。比如之前在特征处理时,用到的多项式方法,会新衍生出多个特征。
不过,多项式回归的可解释性依然是存在的,我们可以使用接get_feature_names来调用生成的新特征矩阵的各个特征上的名称,以便帮助我们解释模型。
线性模型的效果虽然不如随机森林,但是它跑的快……
import numpy as np
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression
X = np.arange(9).reshape(3, 3)
poly = PolynomialFeatures(degree=5).fit(X)
#重要接口get_feature_names
poly.get_feature_names()#打印特征名称
线性还是非线性模型?
原始模型:非线性
![]()
改变特征名称后:线性
![]()
这里需要了解狭义线性模型和广义线性模型。
狭义线性模型:自变量上不能有高此项,自变量与标签之间不能存在非线性关系。(自变量是一次的)
广义线性模型:只要标签与模型拟合出的参数之间的关系是线性的,模型就是线性的。这是说,只要生成的一系列 w之间没有相乘或者相除的关系,我们就认为模型是线性的。(系数w是一次的)
总结一下,多项式回归通常被认为是非线性模型,但广义上它是一种特殊的线性模型,它能够帮助我们处理非线性数据,是线性回归的一种进化。
多项式变化疯狂增加数据维度的同时,也增加了过拟合的可能性,因此多项式变化多与能够处理过拟合的线性模型如岭回归,Lasso等来连用,与在线性回归上使用的效果是一致的。
四、总结
多元线性回归,岭回归,Lasso和多项式回归总计四个算法,他们都是围绕着原始的线性回归进行的拓展和改进。
其中岭回归和Lasso是为了解决多元线性回归中使用最小二乘法的各种限制,主要用途是消除多重共线性带来的影响并且做特征选择。
多项式回归解决了线性回归无法拟合非线性数据的明显缺点,核心作用是提升模型的表现。
由于本人这块也是在跟着学习,所以这块仅仅是做了笔记。以后有时间会再进行整理。