动态规划+柱状图求最大面积问题 85. 最大矩形 84. 柱状图中最大的矩形

85. 最大矩形

给定一个仅包含 0 和 1 的二维二进制矩阵，找出只包含 1 的最大矩形，并返回其面积。

示例:

输入:
[
  ["1","0","1","0","0"],
  ["1","0","1","1","1"],
  ["1","1","1","1","1"],
  ["1","0","0","1","0"]
]
输出: 6

解题
动态规划得到每个点左边连续1的长度，转化为柱状图求最大面积问题；

解法1:每一行得到连续1的长度，求柱形图最大面积
每个位置往下扫一遍；

class Solution {
public:
    int maximalRectangle(vector<vector<char>>& matrix) {
        int n=matrix.size();
        if(!n) return 0;
        int m=matrix[0].size();
        L.resize(n,vector<int>(m,0));  

        for(int i=0;i<n;i++)
            for(int j=0;j<m;j++)
            if(matrix[i][j]=='1'){
                if(j>0) L[i][j]=L[i][j-1]+1;
                else L[i][j]=1;
            }
            
        int maxarea=0;
        int H;
        int tmpi;
        int tmpL;
        for(int i=0;i<n;i++)
            for(int j=0;j<m;j++)
            {
                if(L[i][j])
                {
                    tmpL=L[i][j];
                    tmpi=i;
                    H=0;
                    while(tmpi<n && L[tmpi][j])
                    {
                        tmpL=min(tmpL,L[tmpi][j]);
                        tmpi++;
                        H++;
                    maxarea=max(maxarea,H*tmpL);  //每下一行都要计算一次
                    }
                }
            }
    return maxarea;
    }
private:
vector<vector<int>> L;
};

同方法精简版
每一个位置往上扫一遍，所以偏慢；

class Solution {
public:
    int maximalRectangle(vector<vector<char>>& matrix) {
        int n=matrix.size();
        if(!n) return 0;
        int m=matrix[0].size();
        L.resize(n,vector<int>(m,0));  
        int maxarea=0;
        for(int i=0;i<n;i++)
            for(int j=0;j<m;j++)
            if(matrix[i][j]=='1'){
                if(j>0) L[i][j]=L[i][j-1]+1;
                else L[i][j]=1;

                int width = L[i][j];
                    // compute the maximum area rectangle with a lower right corner at [i, j]
                for(int k = i; k >= 0; k--){
                        width = min(width, L[k][j]);
                        maxarea = max(maxarea, width * (i - k + 1));
            }
        }

    return maxarea;
    }
private:
vector<vector<int>> L;
};

方法2——栈：求最大柱体面积
只需要对每一列遍历一遍即可；

（1）L存放每个点左边连续的1的数量；
（2）遍历L每一列，找到最大面积
用堆栈的方法，减少时间复杂度！

class Solution {
public:
    int maximalRectangle(vector<vector<char>>& matrix) {
        int n=matrix.size();
        if(!n) return 0;
        int m=matrix[0].size();
        L.resize(n,vector<int>(m,0));  
        int maxarea=0;
        for(int i=0;i<n;i++)
            for(int j=0;j<m;j++)
            if(matrix[i][j]=='1'){
                L[i][j]= j>0?L[i][j-1]+1:1;
                maxarea=1;
            }

        stack<int> S;
        S.push(-1);
        int i;
        for(int j=0;j<m;j++)
        {
            for(i=0;i<n;i++)
            {
                while(S.top()!=-1 && L[S.top()][j]>=L[i][j])
                {
                    int tmp=S.top();
                    S.pop();
                    maxarea=max(maxarea,L[tmp][j]*(i-S.top()-1));
                }
                S.push(i);
            }
            while(S.top()!=-1){
                int tmp=S.top();
                    S.pop();
                    maxarea=max(maxarea,L[tmp][j]* (i-S.top()-1));
            }
        }

    return maxarea;
    }
private:
vector<vector<int>> L;
};

84. 柱状图中最大的矩形

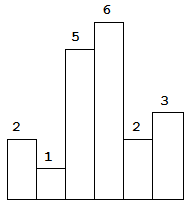
给定 n 个非负整数，用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1 。

求在该柱状图中，能够勾勒出来的矩形的最大面积。

以上是柱状图的示例，其中每个柱子的宽度为 1，给定的高度为 [2,1,5,6,2,3]。

图中阴影部分为所能勾勒出的最大矩形面积，其面积为 10 个单位。

示例:

输入: [2,1,5,6,2,3]
输出: 10

解题
用堆栈，遍历一次即足够；
先在堆栈里放入-1;
顺序放入下标，当栈顶下标对应柱体不低于下一个柱体时，下标出栈，计算该柱体能得到的最大面积maxarea=max(maxarea,heights[tmp]*(i-S.top()-1));，即当前i-出栈的上一个i再-1，乘以出栈的下标对应的柱体高度；
最后清空栈内的元素，矩形长为n-出栈的元素的上一个下标-1，高为出栈元素的高；

class Solution {
public:
    int largestRectangleArea(vector<int>& heights) {
        stack<int> S;
        S.push(-1);
        int n=heights.size();
        if(!n) return 0;
        int maxarea=0;
        for(int i=0;i<n;i++)
        {
            while(S.top()!=-1&&heights[S.top()]>=heights[i])
            {
                int tmp=S.top();
                S.pop();
                maxarea=max(maxarea,heights[tmp]*(i-S.top()-1));
            }
            S.push(i);
        }
        while(S.top()!=-1){
            int tmp=S.top();
            S.pop();
            maxarea=max(maxarea,heights[tmp]*(n-S.top()-1));
        }
        return maxarea;
    }
};