FLANN匹配算法

目录

0 简介

一 算法的选择

1、 随机k-d树算法（The Randomized k-d TreeAlgorithm）

a. Classick-d tree

b.  Randomizedk-d tree

2、  优先搜索k-means树算法（The Priority Search K-MeansTree Algorithm）

2.1  算法描述

3 、层次聚类树 （The Hierarchical ClusteringTree）

二 遍历次数

---

0 简介

FLANN是快速最近邻搜索包（Fast_Library_for_Approximate_Nearest_Neighbors）的简称。它是一个对大数据集和高维特征进行最近邻搜索的算法的集合，而且这些算法都已经被优化过了。在面对大数据集是它的效果要好于BFMatcher。

 

使用FLANN匹配，我们需要传入两个字典作为参数。这两个用来确定要使用的算法和其他相关参数等。

一 算法的选择

第一个是indexParams。配置我们要使用的算法

1、 随机k-d树算法（The Randomized k-d TreeAlgorithm）

a. Classick-d tree

        找出数据集中方差最高的维度，利用这个维度的数值将数据划分为两个部分，对每个子集重复相同的过程。

        参考http://www.cnblogs.com/eyeszjwang/articles/2429382.html。

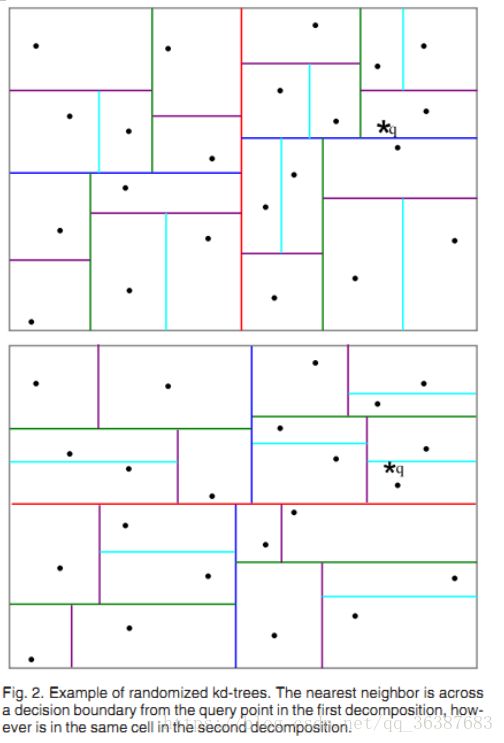
b.  Randomizedk-d tree

        建立多棵随机k-d树，从具有最高方差的N_d维中随机选取若干维度，用来做划分。在对随机k-d森林进行搜索时候，所有的随机k-d树将共享一个优先队列。

       增加树的数量能加快搜索速度，但由于内存负载的问题，树的数量只能控制在一定范围内，比如20，如果超过一定范围，那么搜索速度不会增加甚至会减慢

 

2、  优先搜索k-means树算法（The Priority Search K-MeansTree Algorithm）

        随机k-d森林在许多情形下都很有效，但是对于需要高精度的情形，优先搜索k-means树更加有效。 K-means tree 利用了数据固有的结构信息，它根据数据的所有维度进行聚类，而随机k-d tree一次只利用了一个维度进行划分。

2.1  算法描述

步骤1 建立优先搜索k-means tree:

(1)  建立一个层次化的k-means 树；

(2)  每个层次的聚类中心，作为树的节点；

 

(3)  当某个cluster内的点数量小于K时，那么这些数据节点将做为叶子节点。

步骤2 在优先搜索k-means tree中进行搜索：

(1)  从根节点N开始检索；

(2)  如果是N叶子节点则将同层次的叶子节点都加入到搜索结果中，count += |N|；

(3)  如果N不是叶子节点，则将它的子节点与query Q比较，找出最近的那个节点Cq，同层次的其他节点加入到优先队列中；

(4)  对Cq节点进行递归搜索；

 

(5)  如果优先队列不为空且 count

聚类的个数K，也称为branching factor 是个非常主要的参数。

        建树的时间复杂度 = O( ndKI ( log(n)/log(K) ))  n为数据点的总个数，I为K-means的迭代次数。搜索的时间复杂度 = O( L/K * Kd * ( log(n)/(log(K) ) ) = O(Ld ( log(n)/(log(K) ) )。

3 、层次聚类树 （The Hierarchical ClusteringTree）

        层次聚类树采用k-medoids的聚类方法，而不是k-means。即它的聚类中心总是输入数据的某个点，但是在本算法中，并没有像k-medoids聚类算法那样去最小化方差求聚类中心，而是直接从输入数据中随机选取聚类中心点，这样的方法在建立树时更加简单有效，同时又保持多棵树之间的独立性。

 

        同时建立多棵树，在搜索阶段并行地搜索它们能大大提高搜索性能（归功于随机地选择聚类中心，而不需要多次迭代去获得更好的聚类中心）。建立多棵随机树的方法对k-d tree也十分有效，但对于k-means tree却不适用。

比如我们使用SIFT，我们可以传入参数：

index_params=dict(algorithm = FLANN_INDEX_KDTREE，trees=5)

 

二 遍历次数

第二个字典是SearchParams。它用来指定递归遍历的次数。值越高结果越准确，但是消耗的时间也越多。如果想修改这个值，可以传入参数：

search_params=dict( checks = 10)

 

具体python代码：

import cv2 as cv
import numpy as np
from matplotlib import pyplot as plt


img1 = cv.imread('img/box.png', 0)
img2 = cv.imread('img/box_in_scene.png', 0)

def sift_flann_demo():
    sift = cv.xfeatures2d.SIFT_create()
    kp1, des1 = sift.detectAndCompute(img1, None)
    kp2, des2 = sift.detectAndCompute(img2, None)

    #指定算法
    FLANN_INDEX_KDTREE = 0
    index_params = dict(algorithm = FLANN_INDEX_KDTREE, trees = 5)
    search_params = dict(checks = 50) #指定递归次数

    flann = cv.FlannBasedMatcher(index_params, search_params)
    matches = flann.knnMatch(des1, des2, k=2)
    # Need to draw only good matches, so create a mask
    matchesMask = [[0, 0] for i in range(len(matches))]
    # ratio test as per Lowe's paper
    for i,(m, n) in enumerate(matches):
        if m.distance < 0.7 * n.distance:
            matchesMask[i] = [1, 0]

    draw_params = dict(matchColor = (0, 255, 0),
                       singlePointColor = (255, 0, 0),
                       matchesMask = matchesMask,
                       flags = 0)
    img3 = cv.drawMatchesKnn(img1, kp1, img2, kp2, matches, None, **draw_params)

    cv.namedWindow('img',cv.WINDOW_AUTOSIZE)
    cv.imshow('img',img3)

sift_flann_demo()
cv.waitKey(0)
cv.destroyAllWindows()

结果：