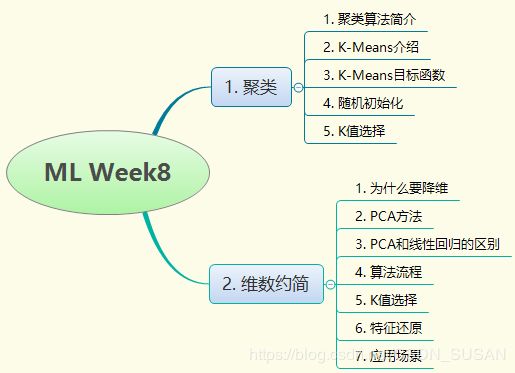
吴恩达机器学习(Machine Learning)课程总结笔记---Week8
文章目录
- 0 概述
- 1. 课程大纲
- 2. 课程内容
- 2.1 聚类
- 2.1.1 聚类算法简介
- 2.1.2 K-Means
- 2.1.3 K-Means目标函数
- 2.1.4 随机初始化
- 2.1.5 K值选择
- 2.2 维数约简
- 2.2.1 为什么要降维
- 2.2.2 PCA方法
- 2.2.3 PCA和线性回归的区别
- 2.2.4 算法流程
- 2.2.5 K的选择
- (1) 尝试法
- (2) 利用奇异值计算
- 2.2.6 特征还原
- 2.2.7 应用场景
- 3. 课后编程作业
- 4. 总结
0 概述
我们知道机器学习主要有三大类学习方法,有监督,无监督和强化学习。之前学习的线性回归,逻辑回归,神经网络、SVM都是有监督学习的典型算法,我们称其为分类或者回归。
本周将就无监督学习,引入一种聚类算法----K-Means。同时,由于实际训练数据会有冗余特征或者我们并不关心的特征,导致数据维度很大,占用内存、影响算法效率,不易于数据可视化,因此引入了一种数据降维的无监督学习----主成分分析法。
下面将就两种方法进行学习。
1. 课程大纲
2. 课程内容
2.1 聚类
2.1.1 聚类算法简介
有监督学习(Supervised Learning)下的训练集:
{ ( x ( 1 ) , y ( 1 ) ) , ( x ( 2 ) , y ( 2 ) ) , ⋯ , ( x ( m ) , y ( m ) ) } \left\{ (x^{(1)},y^{(1)}),(x^{(2)},y^{(2)}),\cdots,(x^{(m)},y^{(m)}) \right\} {(x(1),y(1)),(x(2),y(2)),⋯,(x(m),y(m))}
无监督学习(Unsupervised Learning)下的训练集:
{ ( x ( 1 ) ) , ( x ( 2 ) ) , ( x ( 3 ) ) , ⋯ , ( x ( m ) ) } \left\{ (x^{(1)}),(x^{(2)}),(x^{(3)}),\cdots,(x^{(m)}) \right\} {(x(1)),(x(2)),(x(3)),⋯,(x(m))}
二者区别在于无监督学习,没有标签y来标记它属于哪一类或者等于什么。
在有监督学习中,我们把对样本进行学习的过程称之为分类(Classification),而在无监督学习中,我们将物体被划分到不同集合的过程称之为聚类(Clustering)。聚这个动词十分精确,他传神地描绘了各个物体自主地想属于自己的集合靠拢的过程。
在聚类中,我们把物体所在的集合称之为簇(cluster)。
注意:聚类算法clutering只是无监督学习的一种,不是所有的无监督学习都是聚类算法
2.1.2 K-Means
K-means也是聚类算法中最简单的一种。但是里面包含的思想却是不一般。
下图演示了K-Means聚类的过程,其中k等于2。
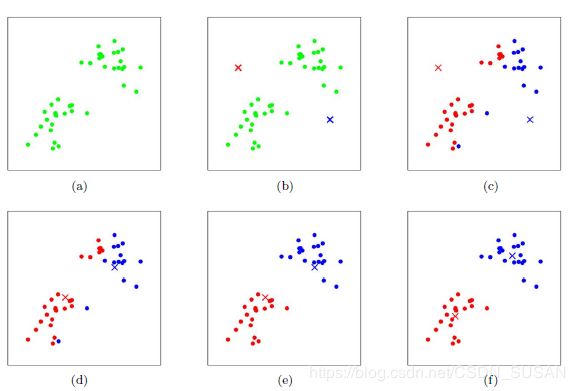
K-means算法是将样本聚类成k个簇(cluster),具体算法不断迭代执行以下两步,直到聚类中心无变化:
- 簇分配 :
在K均值算法的每次循环中,第一步是要进行簇分配,这就是说,我要遍历所有的样本 ,就是图上所有的绿色的点 ,然后依据 每一个点 是更接近红色的这个中心 还是蓝色的这个中心,来将每个数据点分配到两个不同的聚类中心中。 - 移动聚类中心:
我们将两个聚类中心,也就是说红色的叉和蓝色的叉移动到和它一样颜色的那堆点的均值处,那么我们要做的是找出所有红色的点计算出它们的均值,就是所有红色的点 平均下来的位置。然后我们就把红色点的聚类中心移动到蓝色的点也是这样 ,找出所有蓝色的点 计算它们的均值, 把蓝色的叉放到那里。
将按照图上所示这么移动,最终当算法收敛,即聚类中心不再变化时,聚类完成 。
2.1.3 K-Means目标函数
和其他机器学习算法一样,K-Means 也要评估并且最小化聚类代价,在引入 K-Means 的代价函数之前,先引入如下定义:
μ c ( i ) \mu^{(i)}_c μc(i)=样本 x ( i ) x^{(i)} x(i) 被分配到的聚类中心
引入代价函数:
J ( c ( 1 ) , c ( 2 ) , ⋯ , c ( m ) ; μ 1 , μ 2 , ⋯ , μ k ) = 1 m ∑ i = 1 m ∥ x ( i ) − μ c ( i ) ∥ 2 J(c^{(1)},c^{(2)},\cdots,c^{(m)};\mu_1,\mu_2,\cdots,\mu_k)=\frac{1}{m}\sum_{i=1}^m\left \| x^{(i)}-\mu_c(i) \right \|^2 J(c(1),c(2),⋯,c(m);μ1,μ2,⋯,μk)=m1i=1∑m∥∥∥x(i)−μc(i)∥∥∥2
J 也被称为失真代价函数(Distortion Cost Function),可以在调试K均值聚类计算的时候可以看其是否收敛来判断算法是否正常工作。
实际上,K-Means 的两步已经完成了最小化代价函数的过程:
- 样本分配时(簇分配):
我们固定住了 ( μ 1 , μ 2 , ⋯ , μ k ) (\mu_1,\mu_2,\cdots,\mu_k) (μ1,μ2,⋯,μk) ,而关于 ( c ( 1 ) , c ( 2 ) , ⋯ , c ( m ) ) (c^{(1)},c^{(2)},\cdots,c^{(m)}) (c(1),c(2),⋯,c(m)) 最小化了 J 。 - 中心移动时(移动类聚中心):
我们再关于 ( μ 1 , μ 2 , ⋯ , μ k ) (\mu_1,\mu_2,\cdots,\mu_k) (μ1,μ2,⋯,μk) 最小化了 J 。
注意:这个值只会随着迭代下降,不会上升,否则工作就不正常。
2.1.4 随机初始化
在运行K-Means方法钱,首先要初始化所有聚类中心点:
- 我们应该选择K
- 随机选择K个训练实例作为聚类中心。
由于初始化聚类中心的不同,这就可能导致K-Means算法会产生局部最优解。为了解决这个问题,我们可以多次初始化聚类中心,然后计算K-Means的代价函数,根据失真代价函数的大小选择最优解。
2.1.5 K值选择
如何选择聚类数目K是一个很关键的问题,我们在选择的时候,往往要思考我们用这个方法的意义是什么?了解了背后的意义,才能做出正确的选择。
一般而言有两种方式进行K值的选择:
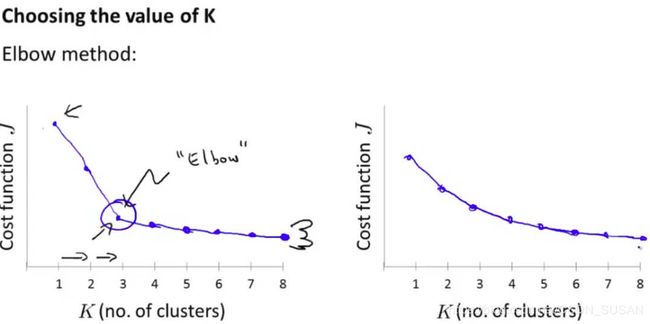
- 肘部法则
如下图,通过观察增加聚类中心的个数,其代价函数是如何变化的。有时候我们可以得到如左边的图像,可以看到在K=3的时候,有一个肘点(Elbow)。因为从1-3,代价函数迅速下降,但是随后下降比较缓慢,所以K=3,也就是分为3个类是一个好的选择。
但很可惜,实际的数据往往没有这么明显的误差变化。
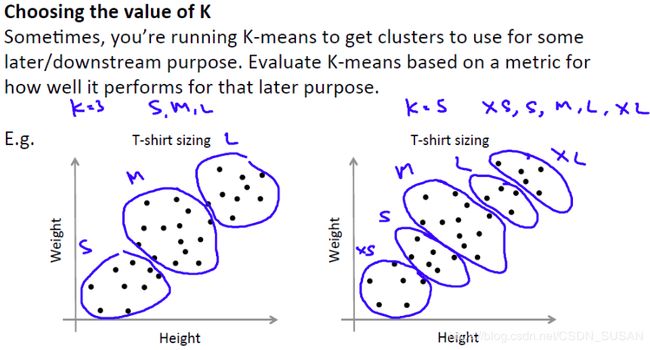
- 根据应用场景定义
如下图我们定义衣服的型号,可以粗略划分为S、M、L好,也可以详细划分XS、S、M、L、XL。
2.2 维数约简
2.2.1 为什么要降维
在机器学习训练过程中,我们希望有足够多的特征(知识)来保准学习模型的训练效果,尤其在图像处理这类的任务中,高维特征是在所难免的,但是,高维的特征也有几个如下不好的地方:
- 学习性能下降,知识越多,吸收知识(输入),并且精通知识(学习)的速度就越慢。
- 过多的特征难于分辨,你很难第一时间认识某个特征代表的意义。
- 特征冗余,厘米和英尺就是一对冗余特征,他们本身代表的意义是一样的,并且能够相互转换。
因此我们可以通过降维,达到两个目的:
- 压缩数据,只保留数据的有用特征
- 数据可视化,帮助更好的认识数据
2.2.2 PCA方法
PCA,Principle Component Analysis,即主成分分析法,是特征降维的最常用手段。顾名思义,PCA 能从冗余特征中提取主要成分,在不太损失模型质量的情况下,提升了模型训练速度。
如下图所示,我们将样本到红色向量的距离称作是投影误差(Projection Error)。以二维投影到一维为例,PCA 就是要找寻一条直线,使得各个特征的投影误差足够小,这样才能尽可能的保留原特征具有的信息。
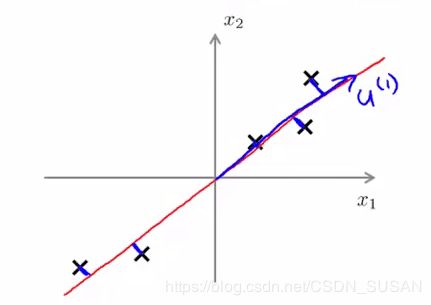
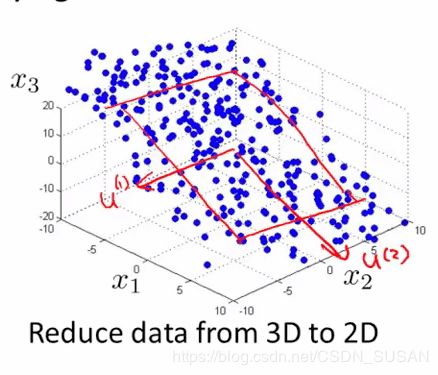
再看三维投影到二维平面的情况,如下图,为了将特征维度从三维降低到二位,PCA 就会先找寻两个三维向量 μ ( 1 ) , μ ( 2 ) \mu^{(1)},\mu^{(2)} μ(1),μ(2) ,二者构成了一个二维平面。
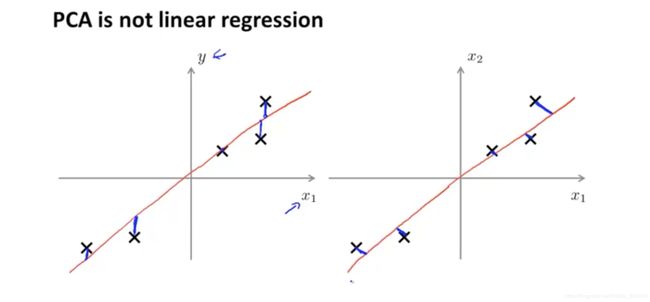
2.2.3 PCA和线性回归的区别
- 线性回归找的是垂直于 X 轴距离最小值,PCA 找的是投影垂直距离最小值。线性回归目的是想通过 x 预测 y,但是 PCA 的目的是为了找一个降维的面,没有什么特殊的 y,代表降维的面的向量 x 1 x_1 x1、 x 2 x_2 x2、 x 3 x_3 x3、 x n x_n xn 都是同等地位的。
- PCA中只有特征没有标签数据y,LR中既有特征样本也有标签数据。
2.2.4 算法流程
假定我们需要将特征维度从 n 维降到 k 维,则 PCA 的执行流程如下:
STEP1 :特征标准化,平衡各个特征尺度:
x j ( i ) = x j ( i ) − μ j s j x^{(i)}_j=\frac{x^{(i)}_j-\mu_j}{s_j} xj(i)=sjxj(i)−μj
μ j \mu_j μj 为特征 j 的均值,sj 为特征 j 的标准差。
STEP2:计算协方差矩阵 $\Sigma $ :
: Σ = 1 m ∑ i = 1 m ( x ( i ) ) ( x ( i ) ) T = 1 m ⋅ X T X \Sigma =\frac{1}{m}\sum_{i=1}{m}(x^{(i)})(x^{(i)})^T=\frac{1}{m} \cdot X^TX Σ=m1∑i=1m(x(i))(x(i))T=m1⋅XTX
STEP3:通过奇异值分解(SVD),求取 $\Sigma $ 的特征向量(eigenvectors):
( U , S , V T ) = S V D ( Σ ) (U,S,V^T)=SVD(\Sigma ) (U,S,VT)=SVD(Σ)
得到矩阵:
U n × n = [ ∣ ∣ ∣ ∣ ∣ u ( 1 ) u ( 2 ) u ( 3 ) … u ( n ) ∣ ∣ ∣ ∣ ∣ ] U_{n \times n}=\left[\begin{array}{ccccc}{ |} & { |} & { |} & { |} & { |} \\ {u^{(1)}} & {u^{(2)}} & {u^{(3)}} & {\dots} & {u^{(n)}} \\ { |} & { |} & { |} & { |} & { |}\end{array}\right] Un×n=⎣⎡∣u(1)∣∣u(2)∣∣u(3)∣∣…∣∣u(n)∣⎦⎤
STEP4:从 U 中取出前 k 个左奇异向量,构成一个约减矩阵 Ureduce :
U r e d u c e = ( u ( 1 ) , u ( 2 ) , ⋯ , μ ( k ) ) U_{reduce}=(u^{(1)},u^{(2)},\cdots,\mu^{(k)}) Ureduce=(u(1),u(2),⋯,μ(k))
STEP5:计算新的特征向量: z ( i ) z^{(i)} z(i)
z = U reduce T x = [ ∣ ∣ ∣ ∣ ∣ u ( 1 ) u ( 2 ) u ( 3 ) … u ( k ) ∣ ∣ ∣ ∣ ] T x z=U_{\text {reduce}}^{T} x=\left[\begin{array}{cccc}{ |} & { |} & { |} & { |} & { |} \\ {u^{(1)}} & {u^{(2)}} & {u^{(3)}} & {\dots} & {u^{(k)}} \\ { |} & { |} & { |} & { |}\end{array}\right]^{T} x z=UreduceTx=⎣⎡∣u(1)∣∣u(2)∣∣u(3)∣∣…∣∣u(k)⎦⎤Tx
2.2.5 K的选择
从 PCA 的执行流程中,我们知道,需要为 PCA 指定目的维度 k 。如果降维不多,则性能提升不大;如果目标维度太小,则又丢失了许多信息。通常,使用如下的流程的来评估 k 值选取值:
(1) 尝试法
选择不同的K值,按如下步骤求解,得到能够满足要求的最小K值。
step1: 求各样本的投影均方误差,PCA 所做的是 尽量最小化 平均平方映射误差 (Average Squared Projection Error) :
min 1 m ∑ j = 1 m ∥ x ( i ) − x a p p r o x ( i ) ∥ 2 \min \frac{1}{m}\sum_{j=1}^{m}\left \| x^{(i)}-x^{(i)}_{approx} \right \|^2 minm1j=1∑m∥∥∥x(i)−xapprox(i)∥∥∥2
step2:求数据的总变差,我还要定义一下 数据的总变差 (Total Variation) 。 它的意思是 “平均来看 我的训练样本 距离零向量多远?
1 m ∑ j = 1 m ∥ x ( i ) ∥ 2 \frac{1}{m}\sum_{j=1}^{m}\left \| x^{(i)} \right \|^2 m1j=1∑m∥∥∥x(i)∥∥∥2
step3:评估下式是否成立:
min 1 m ∑ j = 1 m ∥ x ( i ) − x a p p r o x ( i ) ∥ 2 1 m ∑ j = 1 m ∥ x ( i ) ∥ 2 ⩽ ϵ \frac{\min \frac{1}{m}\sum_{j=1}^{m}\left \| x^{(i)}-x^{(i)}_{approx} \right \|^2}{\frac{1}{m}\sum_{j=1}^{m}\left \| x^{(i)} \right \|^2} \leqslant \epsilon m1∑j=1m∥∥x(i)∥∥2minm1∑j=1m∥∥∥x(i)−xapprox(i)∥∥∥2⩽ϵ
其中, ϵ \epsilon ϵ 的取值可以为 0.01,0.05,0.10,⋯,假设 ϵ = 0.01 \epsilon = 0.01 ϵ=0.01 ,我们就说“特征间 99% 的差异性得到保留”。
(2) 利用奇异值计算
一个更加好的方法是使用SVD对样本的协方差矩阵进行计算,会得到协方差的奇异值

可以通过计算贡献率,求得K:
1 − ∑ i = 1 k S i j ∑ i = 1 n S i j = 1 m ∑ t = 1 m ∥ x ( i ) − x a p p r o x ( i ) ∥ 2 1 m ∑ i − 1 m ∥ x ( i ) ∥ 2 1-\frac{\sum_{i=1}^{k} S_{i j}}{\sum_{i=1}^{n} S_{i j}}=\frac{\frac{1}{m} \sum_{t=1}^{m}\left\|x^{(i)}-x_{a p p r o x}^{(i)}\right\|^{2}}{\frac{1}{m} \sum_{i-1}^{m}\left\|x^{(i)}\right\|^{2}} 1−∑i=1nSij∑i=1kSij=m1∑i−1m∥x(i)∥2m1∑t=1m∥x(i)−xapprox(i)∥2
计算不同的K值对应的贡献率,按照保留原始数据的要求,可以选择合适的K。
2.2.6 特征还原
因为 PCA 仅保留了特征的主成分,所以 PCA 是一种有损的压缩方式,假定我们获得新特征向量为:
z = U r e d u c e T x z=U^T_{reduce}x z=UreduceTx
那么,还原后的特征 x a p p r o x x_{approx} xapprox 为:
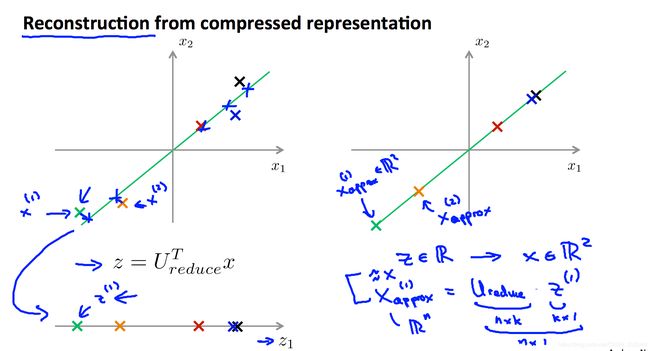
x a p p r o x = U r e d u c e z x_{approx}=U_{reduce}z xapprox=Ureducez
如下图所示:
2.2.7 应用场景
主成份分析法主要有以下用途:
- 数据压缩,减少内存的占用、存储硬盘,加速算法的运转
- 数据可视化:3维2维
误解:
- 有些人觉的PCA也可以用来防止过拟合,但是这是不对的,应该用正则化。原因是PCA不考虑任何与结果变量相关信息,可能丢掉重要特征,而正则化会考虑到结果变量,不会丢失重要数据
- 将PCA作为学习过程的 一部分,这虽然有时候有效,但是依然建议从原始数据开始,只有在必要情况下才考虑使用主成分分析进行降维。
PCA技术的一大好处是对数据进行降维的处理。我们可以对新求出的“主元”向量的重要性进行排序,根据需要取前面最重要的部分,将后面的维数省去,可以达到降维从而简化模型或是对数据进行压缩的效果。同时最大程度的保持了原有数据的信息。
PCA技术的一个很大的优点是,它是完全无参数限制的。在PCA的计算过程中完全不需要人为的设定参数或是根据任何经验模型对计算进行干预,最后的结果只与数据相关,与用户是独立的。
但是,这一点同时也可以看做是缺点。如果用户对观测对象有一定的先验知识,掌握了数据的一些特征,却无法通过参数化等放啊对处理过程进行干预,可能会得不到预期的效果,效率也不高。
3. 课后编程作业
我将课后编程作业的参考答案上传到了github上,包括了octave版本和python版本,大家可参考使用。
https://github.com/GH-SUSAN/Machine-Learning-MarkDown/tree/master/week8
4. 总结
本周针对无监督学习的两类问题,学习两种方法:K-Means和PCA主成分分析法。无监督学习目前在工业场景下应用并没有有监督学习广泛,但是无监督学习是未来很重要的技术爆发点,很值得关注。