【Numerical Optimization】1 基础引入 （Jorge Nocedal 学习笔记）

由于专业方面需要用到各种数值优化的算法，所以最近在学习 Jorge Nocedal 的 《Numerical Optimization》。下面写到的，算是我的学习笔记，应该不会涉及版权问题，算是我自己的总结，也可以与大家讨论分享。

---

数值优化基础

1. 数学基础

所谓优化问题，其实就是（在一定约束条件下）寻找目标方程最小/最大值过程中求解参数的问题，其通用模型如下：

• x x 为变量向量（vector of variables）也就是未知参数（unknowns or parameters）
• f f 是目标函数（objective functions），即要求解其最大/最小值
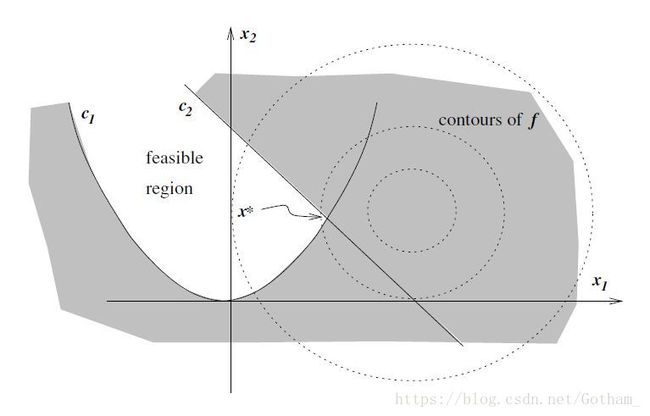
• ci c i 是约束函数（constraint functions），包含等式及不等式约束式（关于 x x 的），用来规定可行域（feasible region）

minx∈Rnf(x),subject.toci(x)=0,i∈εci(x)≥0,i∈ι min x ∈ R n ⁡ f ( x ) , s u b j e c t . t o c i ( x ) = 0 , i ∈ ε c i ( x ) ≥ 0 , i ∈ ι

其中 ε ε 与 ι ι 分别为等式/不等式约束域

可以通过一个例子来理解上述模型：

min(x1−2)2+(x2−1)2,subject.tox21−x2≤0x1+x2≤2 min ( x 1 − 2 ) 2 + ( x 2 − 1 ) 2 , s u b j e c t . t o x 1 2 − x 2 ≤ 0 x 1 + x 2 ≤ 2

将其改写为上述模型定义，即：

f(x)=(x1−2)2+(x2−1)2,x=[x1x2]c(x)=[c1(x)c2(x)]=[−x21+x2−x1−x2+2],ι={1,2},ε=∅ f ( x ) = ( x 1 − 2 ) 2 + ( x 2 − 1 ) 2 , x = [ x 1 x 2 ] c ( x ) = [ c 1 ( x ) c 2 ( x ) ] = [ − x 1 2 + x 2 − x 1 − x 2 + 2 ] , ι = { 1 , 2 } , ε = ∅

2. 数值优化问题的分类

2.1 连续 vs 离散优化

其中离散优化中常用的主要有：

• 整型线性规划 (integer programming)
• 混合整型规划（MIP, Mixed Integer Programming）

这本书主要介绍连续优化问题

2.2 有约束 vs 无约束优化

• 无约束优化（unconstrained optimization）： ι=ε=∅ ι = ε = ∅
• 有约束优化（constrained optimization）： ι≠∅ ι ≠ ∅ OR ε≠∅ ε ≠ ∅

另外引入

• 线性规划（linear programming）:目标方程与约束函数均为关于变量的线性方程
• 非线性规划（non-linear programming）：目标方程和约束函数中至少有一个不是关于变量的线性方程

2.3 全局 vs 局部优化

一般来说，非线性优化问题都在寻找局部最优解，而其全局最优解通常难以找到。而对于 凸规划 问题以及线性规划问题，局部最优解就是全局最优解（凸规划问题之后会写到）。

这本书至针对局部优化问题进行讨论。

2.4 随机 vs 确定性优化

• 随机优化（stochastic optimization）：指带有随机因素的最优化问题，其通常解决方法有以下两种：
  
  • 期望值方法
  • 在置信区间范围内考虑优化

另外为解决模型中的随机因素，还可建立 机会约束优化（chance constrained optimization）模型，或者进行 鲁棒性优化（robust optimization）

在本书中仅考虑有确定参数模型的 确定性优化 （deterministic optimization）

2.5 凸规划

使用以及理解凸规划的意义主要体现在凸规划的两条基本性质上：

• 由于凸规划的可行域为凸集，故凸规划的局部最优解一定是全局最优解
• 当凸规划目标函数为严格凸函数时，若存在最优解，其一定为唯一最优解

这里有一些基本概念需要扫清：

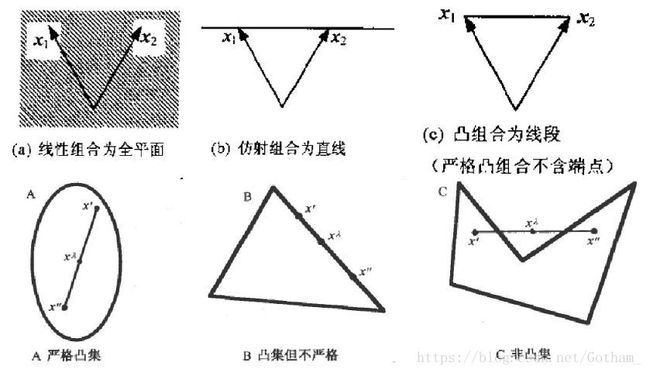
凸集（convex set）

设 S S 为 n 维欧式空间 Rn R n 中的一个集合, 若对 S 中任意两点, 连接它们的线段中任一点仍属于 S S , 那么就说 S S 为一个凸集.
即，对于 S S 中的任意两点 x1 x 1 , x2 x 2 , 对于任意的 λ∈[0,1] λ ∈ [ 0 , 1 ] , 都有

λx1+(1−λ)x2∈S λ x 1 + ( 1 − λ ) x 2 ∈ S

那么称 S S 为一个凸集.。凸集一般用集合 H={x|pTx=α} H = { x | p T x = α } 表示 p p 为n维列向量, α α 为实数。

凸包：是指包含 S S 最小的凸集

凸函数（convex function）

从二维层面看 “凹凸” 可能更符合逻辑经验，一维函数的 “凹凸” 可能与自然逻辑经验相反（最重要的还是从定义出发）

若 x1 x 1 与 x2 x 2 为凸集中任意两点，且 λ∈[0,1] λ ∈ [ 0 , 1 ] 有

f(λx1+(1−λ)x2)≤λf(x1)+(1−λ)f(x2) f ( λ x 1 + ( 1 − λ ) x 2 ) ≤ λ f ( x 1 ) + ( 1 − λ ) f ( x 2 )

则这个函数为凸函数，当 ≤ ≤ 换为 < < 且 λ∈(0,1) λ ∈ ( 0 , 1 ) 时，其为 严格凸函数。典型的凸函数有：单位球以及任何多面体等。
凹函数与严格凹函数的定义与上式正好相反

凸规划（convex programming）

其需要满足的条件如下：

• 目标函数为凸函数
• 等式约束函数为线性函数
• 不等式约束函数为凸函数

其中其可行域一定是凸集（是目标函数凸集与不等式约束函数凸集的交集）

3. 优化算法

文章中对优化算法的描述非常准确：

Optimization algorithms are iterative. They begin with an initial guess of the variable x x and generate a sequence of improved estimates (called “iterates”) until they terminate, hopefully at a solution.

检验其性能的重点：

• 鲁棒性（robustness）
• 效率（efficiency）：time & storage
• 准确率（accuracy）

这些性能指标在多数情况下需要权衡，比如：收敛速度（convergence rate）和资源占用（storage requirement）、鲁棒性和速度等等。