【力扣周赛】194：5440\5441\5442\5443

5440. 数组异或操作

给你两个整数，n 和 start 。
数组 nums 定义为：nums[i] = start + 2*i（下标从 0 开始）且 n == nums.length 。
请返回 nums 中所有元素按位异或（XOR）后得到的结果。

提示：
1 <= n <= 1000
0 <= start <= 1000
n == nums.length

算法

因为不管怎么看都很简单，所以：

class Solution(object):
    def xorOperation(self, n, start):
        res=0
        for i in range(n):
            k=start+2*i
            res^=k
        return res

5441. 保证文件名唯一

给你一个长度为 n 的字符串数组 names 。你将会在文件系统中创建 n 个文件夹：在第 i 分钟，新建名为 names[i] 的文件夹。

由于两个文件 不能 共享相同的文件名，因此如果新建文件夹使用的文件名已经被占用，系统会以 (k) 的形式为新文件夹的文件名添加后缀，其中 k 是能保证文件名唯一的 最小正整数 。

返回长度为 n 的字符串数组，其中 ans[i] 是创建第 i 个文件夹时系统分配给该文件夹的实际名称。

！其实这个保证文件名唯一的描述就是现在计算机里所使用的，唯一让人不熟悉的就是：

输入：names = ["kaido","kaido(1)","kaido","kaido(1)"]
输出：["kaido","kaido(1)","kaido(2)","kaido(1)(1)"]
解释：注意，如果含后缀文件名被占用，那么系统也会按规则在名称后添加新的后缀 (k) 。

提示：
1 <= names.length <= 5 * 10^4
1 <= names[i].length <= 20
names[i] 由小写英文字母、数字和/或圆括号组成。

算法

class Solution(object):
    def getFolderNames(self, names):
    	# res：输出
    	# d：储存已分配的文件名
        res,d = [],{}
        
        for i in names:
        	# 遍历列表，当文件名未分配时，……（见下方省略号段）
            if i in d:
            	# 当文件名已分配时，取出已使用的最小后缀，进入while循环，
            	# 找出未使用的最小后缀，更新最小后缀
                k=d[i][0]
                while k in d[i][1] or '%s(%d)'%(i,k) in d:
                    if k in d:
                        d[i][1].add(k)
                    k+=1
                d[i][0]=k
                d[i][1].add(k)
                i='%s(%d)'%(i,k)
			# ……
			# 未分配时，将当前文件名保存到字典
			# 值域是列表，其中元素0表示当前已使用的最小后缀，元素1是集合，保存所有已使用的后缀
            d[i] = [0, {0}]
            res.append(i)
        return res

5442. 避免洪水泛滥

你的国家有无数个湖泊，所有湖泊一开始都是空的。当第 n 个湖泊下雨的时候，如果第 n 个湖泊是空的，那么它就会装满水，否则这个湖泊会发生洪水。你的目标是避免任意一个湖泊发生洪水。

给你一个整数数组 rains ，其中：

• rains[i] > 0 表示第 i 天时，第 rains[i] 个湖泊会下雨。
• rains[i] == 0 表示第 i 天没有湖泊会下雨，你可以选择 一个 湖泊并 抽干 这个湖泊的水。

请返回一个数组 ans ，满足：

• ans.length == rains.length
• 如果 rains[i] > 0 ，那么ans[i] == -1 。
• 如果 rains[i] == 0 ，ans[i] 是你第 i 天选择抽干的湖泊。

如果有多种可行解，请返回它们中的 任意一个 。如果没办法阻止洪水，请返回一个 空的数组 。

请注意，如果你选择抽干一个装满水的湖泊，它会变成一个空的湖泊。但如果你选择抽干一个空的湖泊，那么将无事发生（详情请看示例 4）。

输入：rains = [69,0,0,0,69]
输出：[-1,69,1,1,-1]
解释：任何形如 [-1,69,x,y,-1], [-1,x,69,y,-1] 或者 [-1,x,y,69,-1] 都是可行的解，其中 1 <= x,y <= 10^9

算法

class Solution(object):
    def avoidFlood(self, rains):
    '''
    res:输出数组
    qian:字典，表示水库是在第几天灌满的
    kong:表示不下雨的日子
    '''
        res=[None]*len(rains)
        qian={}
        kong=[]
        for j,i in enumerate(rains):
            if i>0 :
                if i not in qian:
                    qian[i]=j
                    res[j]=-1
                else:
                    if not kong:return []
                    else:
                        for idx in kong:
                            if idx>qian[i]:
                                kong.remove(idx)
                                break
                        else:
                            return []
                        res[idx]=i
                        res[j]=-1
                        qian[i]=j
            elif i==0:
                kong.append(j)
        for i in kong:
            res[i]=1
        return res

5443. 找到最小生成树里的关键边和伪关键边

给你一个 n 个点的带权无向连通图，节点编号为 0 到 n-1 ，同时还有一个数组 edges ，其中 edges[i] = [fromi, toi, weighti] 表示在 fromi 和 toi 节点之间有一条带权无向边。最小生成树 (MST) 是给定图中边的一个子集，它连接了所有节点且没有环，而且这些边的权值和最小。

请你找到给定图中最小生成树的所有关键边和伪关键边。如果最小生成树中删去某条边，会导致最小生成树的权值和增加，那么我们就说它是一条关键边。伪关键边则是可能会出现在某些最小生成树中但不会出现在所有最小生成树中的边。

请注意，你可以分别以任意顺序返回关键边的下标和伪关键边的下标。

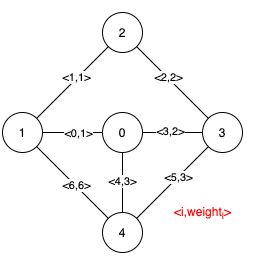
输入：n = 5, edges = [[0,1,1],[1,2,1],[2,3,2],[0,3,2],[0,4,3],[3,4,3],[1,4,6]]
输出：[[0,1],[2,3,4,5]]
解释：上图描述了给定图。
下图是所有的最小生成树。

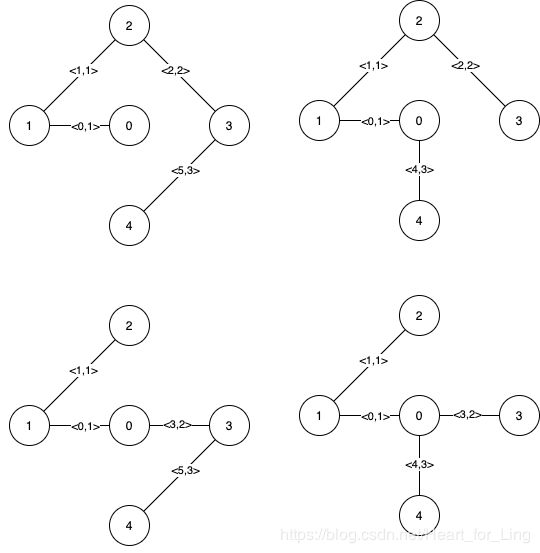
注意到第 0 条边和第 1 条边出现在了所有最小生成树中，所以它们是关键边，我们将这两个下标作为输出的第一个列表。
边 2，3，4 和 5 是所有 MST 的剩余边，所以它们是伪关键边。我们将它们作为输出的第二个列表。

算法

在图这方面还是很不熟练啊，暂且搁置，日后填坑。

总结

日常丢人。