维纳滤波器自适应算法-SD与LMS算法(附Matlab代码)
本文首发在我的个人博客“宅到没朋友”,欢迎来玩!http://www.weekreport.cn/archives/481
1.维纳滤波器基本理论
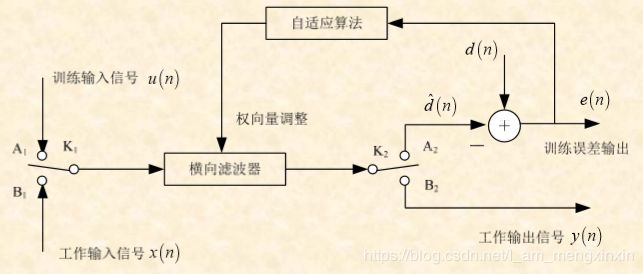
- 学习过程:K1打向A1,K2打向A2,求取横向滤波器最优权向量。
- 工作过程:K1打向B1,K2打向B2,对输入信号进行滤波处理。
上述两个过程中,求滤波器最优权向量的学习过程是最优滤波的关键!
上图中的横向滤波器结构如下图,学习过程的任务就是求最优权向量 w ⃗ = [ w 0 w 1 ⋯ w M − 1 ] T \vec{w}=\left[ w_{0} \quad w_{1} \cdots w_{M-1} \right]^{T} w=[w0w1⋯wM−1]T
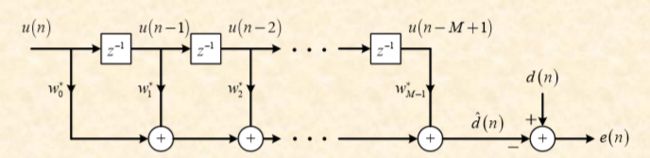
- d ( n ) d\left(n\right) d(n):期望响应
- d ^ ( n ) \hat{d}\left(n\right) d^(n):对期望响应的估计, d ^ ( n ) = ∑ i = 0 M − 1 w i u ( n − i ) = w ⃗ H u ⃗ ( n ) = u ⃗ T ( n ) w ⃗ n \hat{d}\left(n\right) = \sum_{i=0}^{M-1}w_{i}^{}u\left(n-i\right )=\vec{w}^{H}\vec{u}\left(n \right )=\vec{u}^{T}\left(n \right )\vec{w}^{n} d^(n)=∑i=0M−1wiu(n−i)=wHu(n)=uT(n)wn
- e ( n ) e\left( n \right) e(n):估计误差, e ( n ) = d ( n ) − d ^ ( n ) e\left(n\right) = d\left(n\right)-\hat{d}\left(n\right) e(n)=d(n)−d^(n)
定义 E ( n ) E\left(n\right) E(n)的平均功率为:
J ( w ) = { ∣ e ( n ) ∣ 2 } = σ d 2 − p ⃗ H w ⃗ − w ⃗ H p ⃗ + w ⃗ H R w ⃗ ( 1 ) J\left(w\right)=\left\{ \left|e \left(n \right)\right|^{2}\right\}=\sigma_{d}^{2}-\vec{p}^{H}\vec{w}-\vec{w}^{H}\vec{p}+\vec{w}^{H}R\vec{w}\quad(1) J(w)={∣e(n)∣2}=σd2−pHw−wHp+wHRw(1)
其中:
- d ( n ) d\left( n \right) d(n)的平均功率为: σ d 2 = E { ∣ d ( n ) ∣ 2 } \sigma_{d}^{2}=E\left\{\left|d\left(n\right)\right|^{2}\right\} σd2=E{∣d(n)∣2}。
- 互相关向量: p = E { u ⃗ ( n ) d ∗ ( n ) } p=E\left\{\vec{u}\left(n\right)d^{*}\left(n\right)\right\} p=E{u(n)d∗(n)}。
- u ( n ) u\left(n\right) u(n)的自相关矩阵: R = E { u ⃗ ( n ) u ⃗ H ( n ) } R=E\left\{\vec{u}\left(n\right)\vec{u}^{H}\left(n\right)\right\} R=E{u(n)uH(n)}。
J ( w ⃗ ) J\left(\vec{w}\right) J(w)也被称为误差性能面或者均方误差。
利用凸优化知识对 J ( w ⃗ ) J\left(\vec{w}\right) J(w)求梯度并令梯度为0,即:
▽ J ( w ⃗ ) = − 2 p ⃗ + 2 R w ⃗ = 0 ( 2 ) \bigtriangledown J\left ( \vec{w} \right )=-2\vec{p}+2R\vec{w}=0\quad(2) ▽J(w)=−2p+2Rw=0(2)
化简得到维纳-霍夫方程:
R w 0 ⃗ = p ⃗ ( 3 ) R\vec{w_{0}}=\vec{p}\quad(3) Rw0=p(3)
R R R是非奇异的,方程两边同时乘以 R − 1 R^{-1} R−1得到最优权向量 w ⃗ 0 \vec{w}_{0} w0
w 0 ⃗ = R − 1 p ⃗ ( 4 ) \vec{w_{0}} = R^{-1}\vec{p}\quad(4) w0=R−1p(4)
2.维纳滤波自适应算法
直接利用维纳-霍夫方程求滤波器的最优权向量涉及矩阵求逆 ( R − 1 ) (R^{-1}) (R−1),计算量大,工程上实现困难!使用自适应算法替代矩阵求逆去调整 w ⃗ ( n ) \vec{w}\left(n\right) w(n),使得误差最小。
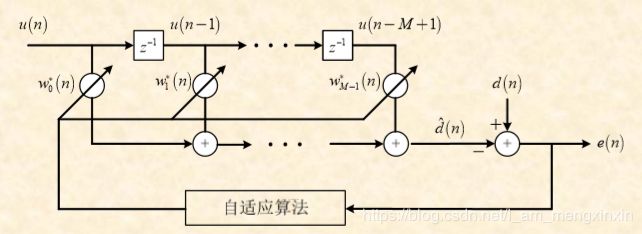
2.1 最陡下降算法(SD)
沿着 J ( w ⃗ ) J\left(\vec{w}\right) J(w)的负梯度方向调整权向量 w ⃗ \vec{w} w以寻求最优权向量。
w ⃗ ( n + 1 ) = w ⃗ ( n ) + Δ w ⃗ ( 5 ) \vec{w}\left(n+1\right)=\vec{w}\left(n\right)+\vec{\Delta w}\quad(5) w(n+1)=w(n)+Δw(5)
Δ w ⃗ = − 1 2 μ ▽ J ( w ⃗ ( n ) ) ( 6 ) \vec{\Delta w}=-\frac{1}{2} \mu \bigtriangledown J\left(\vec{w}\left(n\right)\right)\quad(6) Δw=−21μ▽J(w(n))(6)
由式(2)、(5)、(6)可以得到:
w ⃗ ( n + 1 ) = w ⃗ ( n ) + μ [ p ⃗ − R w ⃗ ( n ) ] ( 7 ) \vec{w}\left(n+1\right)=\vec{w}\left(n\right)+\mu \left[\vec{p}-R\vec{w}\left(n\right)\right]\quad(7) w(n+1)=w(n)+μ[p−Rw(n)](7)
μ > 0 \mu>0 μ>0被称为步长参数或步长因子,该参数对自适应算法发迭代速度有很大影响。
2.2 LMS(最小均方)算法
由(7)式可知:
- 若互相关向量p和自相关矩阵R确定,SD算法的迭代过程和结果就已经确定;
- SD算法基于统计和概率的思想,其结果与输入信号的变化无关,不具有自适应性。
对于平稳随机信号,若该信号是各态历经(均方遍历)的,则可用时间平均代替统计平均,用时间自相关代替统计自相关。
R ≐ R ^ = 1 N ∑ i = 1 N u ( i ) u H ( i ) = u ⃗ ( n ) u ⃗ H ( n ) ( 8 ) R\doteq\hat{R}=\frac{1}{N}\sum_{i=1}^{N}u\left(i\right)u^{H}\left(i\right)=\vec{u}\left(n\right)\vec{u}^{H}\left(n\right)\quad(8) R≐R^=N1i=1∑Nu(i)uH(i)=u(n)uH(n)(8)
p ⃗ ≐ p ^ ⃗ = 1 N ∑ i = 1 N u ( i ) d ∗ ( i ) = u ⃗ ( n ) d ∗ ( n ) ( 9 ) \vec{p}\doteq\vec{\hat{p}}=\frac{1}{N}\sum_{i=1}^{N}u\left(i\right)d^{*}\left(i\right)=\vec{u}\left(n\right)d^{*}\left(n\right)\quad(9) p≐p^=N1i=1∑Nu(i)d∗(i)=u(n)d∗(n)(9)
由式(7)、(8)、(9)可得:
w ^ ⃗ ( n + 1 ) = w ^ ⃗ ( n ) + μ u ⃗ ( n ) e ∗ ( n ) ( 10 ) \vec{\hat{w}}(n+1) =\vec{ \hat{w}}\left(n\right)+\mu \vec{u}\left(n\right)e^{*}\left(n\right)\quad(10) w^(n+1)=w^(n)+μu(n)e∗(n)(10)
(10)式就是LMS算法的迭代过程。
2.2.1 LMS算法与SD算法的区别与联系
- SD算法中,互相关向量 p ⃗ \vec{p} p和自相关矩阵 R R R都是确定量,得到的 w ⃗ ( n ) \vec{w}\left(n\right) w(n)是确定的向量序列。
- LMS算法中, u ⃗ ( n ) \vec{u}\left(n\right) u(n)和 e ⃗ ( n ) \vec{e}\left(n\right) e(n)都是随机过程,所以 w ^ ⃗ ( n ) \vec{\hat{w}}\left(n\right) w^(n)是随机向量。
- LMS算法是一种随机梯度算法。
▽ ^ J ( n ) = − 2 p ^ ⃗ + 2 R ^ w ⃗ ( n ) = − 2 u ⃗ ( n ) e ∗ ( n ) \hat{\bigtriangledown}J\left(n\right)=-2\vec{\hat{p}}+2\hat{R}\vec{w}\left(n\right)=-2\vec{u}(n)e^{*}(n) ▽^J(n)=−2p^+2R^w(n)=−2u(n)e∗(n)
2.2.2 LMS算法步骤
- 初始化:n=0
权向量: w ^ ⃗ ( 0 ) = 0 ⃗ \vec{\hat{w}}(0)=\vec{0} w^(0)=0
估计误差: e ( 0 ) = d ( 0 ) − d ^ ( 0 ) = d ( 0 ) e(0) = d(0)-\hat{d}(0)=d(0) e(0)=d(0)−d^(0)=d(0)
输入向量: u ⃗ ( 0 ) = [ u ( 0 ) u ( − 1 ) ⋯ u ( − M + 1 ) ] T = [ u ( 0 ) 0 ⋯ 0 ] T \vec{u}(0)=[u(0)\quad u(-1) \cdots u(-M+1)]^{T}=[u(0)\quad 0 \cdots 0]^{T} u(0)=[u(0)u(−1)⋯u(−M+1)]T=[u(0)0⋯0]T - n=0,1,2…
更新权向量: w ^ ⃗ ( n + 1 ) = w ^ ⃗ ( n ) + μ u ⃗ ( n ) e ∗ ( n ) \vec{\hat{w}}(n+1) =\vec{ \hat{w}}\left(n\right)+\mu \vec{u}\left(n\right)e^{*}\left(n\right) w^(n+1)=w^(n)+μu(n)e∗(n)
更新期望信号的估计: d ^ ( n + 1 ) = w ^ ⃗ H ( n + 1 ) u ⃗ ( n + 1 ) \hat{d}(n+1)=\vec{\hat{w}}^{H}(n+1)\vec{u}(n+1) d^(n+1)=w^H(n+1)u(n+1)
更新估计误差: e ( n + 1 ) = d ( n + 1 ) − d ^ ( n + 1 ) ) e(n+1)=d(n+1)-\hat{d}(n+1)) e(n+1)=d(n+1)−d^(n+1)) - 令n=n+1,转到步骤2。
3.算例
(1):产生512点AR过程样本序列。(样本序列为512点时μ=0.005的迭代过程尚未收敛,所以实验分别用512点和512*4点做了对比试验)
(2):在不同步长情况下(μ=0.05和μ=0.005)用LMS滤波器估计w1和w2。
(3):在(2)的条件下进行100次独立实验计算剩余均方误差和失调参数,并画出学习曲线。
(4):比较μ=0.05和μ=0.005时二者学习曲线的区别。
4.Matlab仿真结果
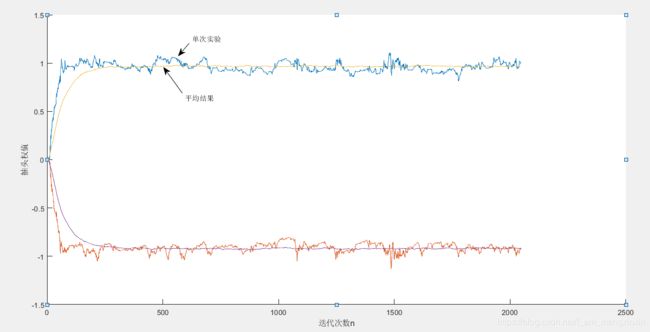
图2 滤波器权系数迭代(N=5124,μ=0.05)
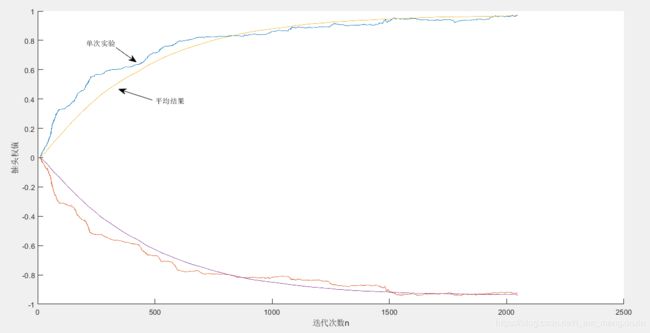
图3 滤波器权系数(N=5124,μ=0.005)
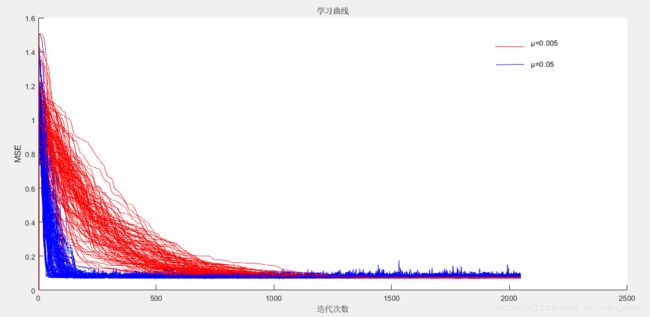
图4 学习曲线(N=512*4)
| 步长 | J(∞) | J | M |
| μ=0.05 | 0.0038 | 0.0052 | 0.0516 |
| μ=0.005 | 0.0004 | 0.0004 | 0.0049 |
由表1可以看到当样本点数足够多时,得到的剩余均方误差J可以较好的逼近J(∞)。
由图4和表1可以看到μ=0.005的学习曲线收敛的较慢,μ=0.05的学习曲线收敛的较快,但μ=0.005的学习曲线最后收敛的值更小,即误差更小。还可以看到μ越小,失调参数M越小,稳定性能更好。
5.Matlab源码
点此下载源码!