北航操作系统课程-第五次作业-虚拟内存管理-页面置换
北航操作系统课程-第五次作业-虚拟内存管理-页面置换
北京航空航天大学计算机学院-2020春操作系统课程
题目作者为北航计算机学院操作系统课程组,答案为博主原创。水平有限,无法保证作答正确性,如有错误敬请批评指正。部分作答源自百度谷歌等其他资料,如有侵权联系删除
经评论区的朋友Zars19指出,第三题在设计OPT算法时忽略了对于预测未来页面使用情况而言必须要每一次都更新要替换的页面,在页面命中时也要更新,已经更正,感谢Zars19。
另外经课程同学提示,第五题混淆了按按字寻址和字节寻址,忽略了大小端的不同情况,也已经更正。
1 叙述缺页中断的处理流程。
当进程执行中需访问的页面不在物理内存中时,会引发发生缺页中断(也称缺页异常),进行所需页面换入,步骤如下:
-
陷入内核态,保存必要的信息(OS及用户进程状态相关的信息)。(现场保护)
-
查找出发生缺页中断的虚拟页面(进程地址空间中的页面)。这个虚拟页面的信息通常会保存在一个硬件寄存器中,如果没有的话,操作系统必须检索程序计数器,取出这条指令,用软件分析该指令,通过分析找出发生页面中断的虚拟页面。(页面定位)
-
检查虚拟地址的有效性及安全保护位。如果发生保护错误,则杀死该进程。(权限检查)
-
查找一个空闲的页框(物理内存中的页面),如果没有空闲页框则需要通过页面置换算法找到一个需要换出
的页框。(新页面调入(1)) -
如果找的页框中的内容被修改了,则需要将修改的内容保存到磁盘上¹。(注:此时需要将页框置为忙状态,以防页框被其它进程抢占掉)(旧页面写回)
-
页框“干净”后,操作系统将保持在磁盘上的页面内容复制到该页框中²。(新页面调入(2))
步骤5,6会引起写磁盘调用,发生上下文切换(在等待磁盘写的过程中让其它进程运行)。
-
当磁盘中的页面内容全部装入页框后,向CPU发送一个中断。操作系统更新内存中的页表项,将虚拟页面映射的页框号更新为写入的页框,并将页框标记为正常状态。(更新页表)
-
恢复缺页中断发生前的状态,将程序指针重新指向引起缺页中断的指令。(恢复现场)
-
程序重新执行引发缺页中断的指令,进行存储访问。(继续执行)
2 假设页面的访问存在一定的周期性循环,但周期之间会随机出现一些页面的访问。例如:0, 1, 2, …, 511, 431, 0, 1, 2, …, 511, 332, 0, 1, 2, …, 511, …, 请思考:
- LRU、FIFO和Clock算法的效果如何?
- 如果有500个页框,能否设计一个优于LRU、FIFO和Clock的算法?
在题目所述得情况下,一共有512个可能得页面需要装载,因此若物理页框数大于512,那么不管哪种算法都不会产生缺页中断,LUR、FIFO和Clock算法得效果是相同的(事实上他们都没有应用过)。
如果物理页框数不足512个,那么三种算法的效果也是几乎等同的。在首先装满所有物理页框之后,对于FIFO而言,在需要淘汰物理页的时候会从首先装入,即周期性循环中最靠前的物理页开始淘汰,不及该循环中的物理页再次出现,它一定会被淘汰,从而FIFO在应对这种情况的循环时,除了那个随机出现的页面之外,所有页面都会缺页。对于Clock算法而言情况也并不会太好,Clock在FIFO的原则之上给页面“第二次机会”,即如果一个页面装入后被再次访问过,就“再给它一次生存的机会”,但在上述情况中等待被淘汰的物理页大概率均不会有装入内存后的第二次访问机会,随机出现的页面可能会有再次访问从而享受到Clock的“庇护”,但大部分页面大概率都会缺页。对于LRU而言,它的效果也和前两者几乎等同,这是因为LRU淘汰最久没有用到的页面,在题目所述的循环中最久不用的页面和最先到来的页面几乎是等价的,因此LRU也会面临几乎所有页面都缺页的窘境。
综上所述,面临题目所述的周期性页面访问时,LRU、FIFO和Clock的效果几乎一致,在页框足够时不会产生任何缺页,但在页框不足时几乎每次访问都会缺页,缺页率接近100%。
针对周期性页面访问,在物理页框不足的情况下,使用与FIFO先进先出完全相对的“FILO 先进后出”(或后进先出)算法,其性能会大大优于LRU、FIFO和Clock。在最初的500个物理页被占满之后,到来的第500号虚拟页会替换掉499号,第501号又会替换500,等等,在此第500-511号虚拟页会全部缺页,但在新的循环到来时,前499个虚拟页会全部命中,夹在两次循环之间的随机页也会有500/512的概率命中,缺页率降至约为12/512=2.34%,远远优于LRU、FIFO和Clock。
3 假设有10个页面,n个页框。页面的访问顺序为0, 9, 8, 4, 4, 3, 6, 5, 1, 5, 0, 2, 1, 1, 1, 1, 8, 8, 5, 3, 9, 8, 9, 9, 6, 1, 8, 4, 6, 4, 3, 7, 1, 3, 2, 9, 8, 6, 2, 9, 2, 7, 2, 7, 8, 4, 2, 3, 0, 1, 9, 4, 7, 1, 5, 9, 1, 7, 3, 4, 3, 7, 1, 0, 3, 5, 9, 9, 4, 9, 6, 1, 7, 5, 9, 4, 9, 7, 3, 6, 7, 7, 4, 5, 3, 5, 3, 1, 5, 6, 1, 1, 9, 6, 6, 4, 0, 9, 4, 3。当n在[1,10]中取值时,请编写程序实现OPT、LRU、FIFO页面置换算法,并根据页面访问顺序模拟执行,分别计算缺页数量,画出缺页数量随页框数n的变化曲线(3条线)。
以下使用python计算三种页面置换算法,OPT算法如下,循环访问页面的数组,如遇页面命中则跳过,未命中则给缺页中断数计数,并基于已知的页面访问顺序预测最优替换情况——检测出哪一页面在未来最晚被用到,然后替换之。
def opt_to_replace(i, frame_usage):
future_list = page_visit_list[i+1:]
to_replace = frame_usage[0]
next_use = 0
for page in frame_usage:
if page in future_list:
if future_list.index(page) > next_use:
to_replace = page
next_use = future_list.index(page)
else:
to_replace = page
break
return to_replace
def opt(frame_num):
page_fault = 0
frame_usage = []
to_replace = 0
for i in range(len(page_visit_list)):
page = page_visit_list[i]
if page in frame_usage:
to_replace = opt_to_replace(i, frame_usage)
continue
page_fault = page_fault + 1
if len(frame_usage) < frame_num:
frame_usage.append(page)
to_replace = opt_to_replace(i, frame_usage)
continue
frame_usage[frame_usage.index(to_replace)] = page
to_replace = opt_to_replace(i, frame_usage)
return page_fault
LRU算法与FIFO算法实现思路大致相同,区别在于当页命中时,LRU会将命中的页移至淘汰序列队尾,而FIFO不会,仍然按照先进先出原则不改变队列。
def lru(frame_num):
page_fault = 0
frame_usage = []
for page in page_visit_list:
if page in frame_usage:
frame_usage.remove(page)
frame_usage.append(page)
continue
page_fault = page_fault + 1
if len(frame_usage) < frame_num:
frame_usage.append(page)
continue
frame_usage.remove(frame_usage[0])
frame_usage.append(page)
return page_fault
def fifo(frame_num):
page_fault = 0
frame_usage = []
for page in page_visit_list:
if page in frame_usage:
continue
page_fault = page_fault + 1
if len(frame_usage) < frame_num:
frame_usage.append(page)
continue
frame_usage.remove(frame_usage[0])
frame_usage.append(page)
return page_fault
最终利用python的matplotlib绘制了三种算法,改变物理页框数量的缺页数趋势图,绘图有关代码在此略去,本题完整代码见文件结尾附件。
最终计算得到三种算法的缺页数如下表:
| 物理页框数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
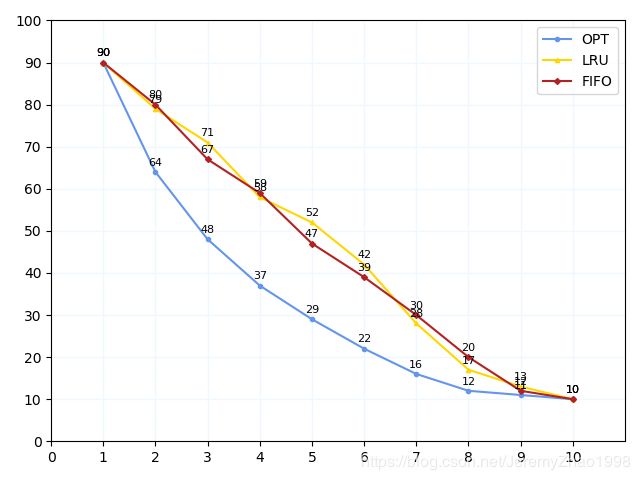
| OPT | 90 | 64 | 48 | 37 | 29 | 22 | 16 | 12 | 11 | 10 |
| LRU | 90 | 79 | 71 | 58 | 52 | 42 | 28 | 17 | 13 | 10 |
| FIFO | 90 | 80 | 67 | 59 | 47 | 39 | 30 | 20 | 12 | 10 |
绘制图像结果如下:
4 一个32位的虚拟存储系统有两级页表,其逻辑地址中,第22到31位是第一级页表,12位到21位是第二级页表,页内偏移占0到11位。一个进程的地址空间为4GB,如果从0x80000000开始映射4MB大小页表空间,请问第一级页表所占4KB空间的起始地址?并说明理由。(注意B代表字节,一个32位地址占4字节)
此题考查页目录自映射机制。在32位4GB地址空间中采用二级页表机制,页内偏移占12位,代表着每一页大小为4KB,因此4GB地址空间一共被分为2^20个页,每个页需要一个页表项,而页表空间占用了4MB,因此每个页表项占用了4B。采用二级页表机制,页目录(第一级页表)占用10位地址,可以检索到1024个页表,每个页表检索1024个页面,因而第二级页表占用10位地址。页目录本身占用4KB空间,说明每个页目录项与每个页表项一样,占用4B内容,而页目录本身恰好是一个页面的大小,因此可以使用页目录自映射机制,将页目录恰好安置在一个页面上,该页称作页目录页;每个页表也恰好安置在一个页面上,该页称作页表页。
将4MB的第二级页表看作对整个4GB内存空间的压缩映射,其起始地址是0x8000_0000,那么所有1024个第二级级页表页中,必然有一个页表页映射的是4MB第二级页表空间,这个页表页和页目录的功能和内容完全重合,将其作为页目录即可节省4KB一个页面的页目录空间,这就是页目录自映射机制。
我们已经知道4MB第二级页表空间对于整个4GB内存空间是线性映射的,其起始地址是0x8000_0000,那么要寻找页目录起始地址,只需要知道页目录所映射的内存相对于整个内存布局在什么位置,再加上第二季页表起始地址即可。页目录所映射的就是第二级页表空间,其起始地址是0x8000_0000,其之前有0x8000_0000 >> 12 = 0x8_0000个页,每个页在页表中占4B的页表项空间,所以页目录所映射的内存相对于整个内存在第二级页表中的偏移量为 0x8_0000 * 4 = 0x20_0000。页目录起始地址即为 0x8000_0000 + 0x20_0000 = 0x8020_0000。
综上总结,在32位4GB地址空间,4KB页面大小,采用二级页表机制,其页表起始地址和页目录起始地址的关系为: P D b a s e = P T b a s e + P T b a s e > > 10 PD_{base} = PT_{base} + PT_{base} >> 10 PDbase=PTbase+PTbase>>10 。在0x8000_0000处映射页表,那么页目录起始地址为 0x8020_0000。
5 一个32位的虚拟存储系统有两级页表,其逻辑地址中,第22到31位是第一级页表(页目录)的索引,第12位到21位是第二级页表的索引,页内偏移占第0到11位。每个页表(目录)项包含20位物理页框号和12位标志位,其中最后1位为页有效位。
虚拟地址格式:
| 10位 | 10位 | 12位 |
|---|---|---|
| 页目录号 | 二级页表号 | 页内偏移量 |
页目录项、页表项格式:
| 20位 | 11位 | 1位 |
|---|---|---|
| 物理页框号 | 其他页面标志 | 页面有效标志 |
-
请问进程整个的地址空间有多少字节?一页有多少字节?
-
如果当前进程的页目录物理基地址、页目录和相应页表内容如图下所示:
页目录物理地址:0x1000 页表物理地址:0x5000 页表物理地址:0x2_0000 0000: 0x0 0000: 0x0 0000: 0x9000 0001: 0x1001 0001: 0x4_e001 0001: 0x32_6001 0002: 0x5001 0002: 0x6_7001 0002: 0x4_1001 0003: 0x2_0001 0003: 0x2_0001 0003: 0x0 0004: 0x0 0004: 0x0 0004: 0x0 … … … 1023: 0x0 1023: 0x0 1023: 0x0 描述访问以下虚拟地址时系统进行地址转换的过程,如可行给出最终访存获取到的数据。虚拟地址:0x0、0x00803004、0x00402001
-
条件如上,若要访问物理地址0x326028,需要使用哪个虚拟地址?
32位地址,进程地址空间共4GB;页内偏移量12位,每一页有4KB大小。
根据上图的页目录和页表内容,访问0x0时先查页目录项0000:有效标志为0,页面尚未装入,引发缺页中断。
根据上图的页目录和页表内容,访问0x0080_3004 = 0b0000_0000_1000_0000_0011_0000_0000_0100,页目录位0b00_0000_0010,查页目录项0002:有效标志为1,页表物理地址0x5000。原地址页表位0b00_0000_0011,查0x5000处的页表项0003:0x2_0001,有效标志为1,页面物理地址为0x2_0000。原地址页内偏移位0b0000_0000_0100,系统为大端和小端访问到的数据分别为0b0000_0000和0b0000_0001。
根据上图的页目录和页表内容,访问0x0040_2001 = 0b0000_0000_0100_0000_0010_0000_0000_0001,页目录位0b00_0000_0001,查页目录项0001:有效标志为1,页表物理地址0x1000。原地址页表位0b00_0000_0010,查0x1000处,即页目录本身的页表项(页目录项)0002:0x5001,有效标志为1,页面物理地址为0x5000。原地址页内偏移位0b0000_0000_0001,系统为大端和小端访问到的数据都会是0b0000_0000。
若要访问物理地址0x32_6028,该物理地址的低12位0x028是页内偏移,物理页框号0x32_6000,可知虚拟地址页内偏移位为0b0000_0010_1000。在上图所示的页表内容中查到0x2_0000处页表的0001偏移处存有该物理页框号且有效位为1,可知虚拟地址的页表偏移位为0b00_0000_0001。从页目录中查到页目录项0003中页表物理地址为0x2_0000且标志位为1,可知虚拟地址页目录位为0b00_0000_0011。综上,虚拟地址为0b0000_0000_1100_0000_0001_0000_0010_1000,即0x00c0_1028.
附件:第3题页面置换完整代码
# -*- coding: utf-8 -*-
# @Time : 2020/3/25 21:30
# @Author : JeremyZhao1998
# @File : PageReplacement.py
# @Software : PyCharm
# @Description: To illustrate OPT, LRU and FIFO algorithm in page replacement.
import GraphPlot
page_visit_list = [0, 9, 8, 4, 4, 3, 6, 5, 1, 5,
0, 2, 1, 1, 1, 1, 8, 8, 5, 3,
9, 8, 9, 9, 6, 1, 8, 4, 6, 4,
3, 7, 1, 3, 2, 9, 8, 6, 2, 9,
2, 7, 2, 7, 8, 4, 2, 3, 0, 1,
9, 4, 7, 1, 5, 9, 1, 7, 3, 4,
3, 7, 1, 0, 3, 5, 9, 9, 4, 9,
6, 1, 7, 5, 9, 4, 9, 7, 3, 6,
7, 7, 4, 5, 3, 5, 3, 1, 5, 6,
1, 1, 9, 6, 6, 4, 0, 9, 4, 3]
def opt_to_replace(i, frame_usage):
future_list = page_visit_list[i+1:]
to_replace = frame_usage[0]
next_use = 0
for page in frame_usage:
if page in future_list:
if future_list.index(page) > next_use:
to_replace = page
next_use = future_list.index(page)
else:
to_replace = page
break
return to_replace
def opt(frame_num):
page_fault = 0
frame_usage = []
to_replace = 0
for i in range(len(page_visit_list)):
page = page_visit_list[i]
if page in frame_usage:
to_replace = opt_to_replace(i, frame_usage)
continue
page_fault = page_fault + 1
if len(frame_usage) < frame_num:
frame_usage.append(page)
to_replace = opt_to_replace(i, frame_usage)
continue
frame_usage[frame_usage.index(to_replace)] = page
to_replace = opt_to_replace(i, frame_usage)
return page_fault
def lru(frame_num):
page_fault = 0
frame_usage = []
for page in page_visit_list:
if page in frame_usage:
frame_usage.remove(page)
frame_usage.append(page)
continue
page_fault = page_fault + 1
if len(frame_usage) < frame_num:
frame_usage.append(page)
continue
frame_usage.remove(frame_usage[0])
frame_usage.append(page)
return page_fault
def fifo(frame_num):
page_fault = 0
frame_usage = []
for page in page_visit_list:
if page in frame_usage:
continue
page_fault = page_fault + 1
if len(frame_usage) < frame_num:
frame_usage.append(page)
continue
frame_usage.remove(frame_usage[0])
frame_usage.append(page)
return page_fault
if __name__ == '__main__':
opt_faults, lru_faults, fifo_faults = [], [], []
for i in range(10):
opt_faults.append(opt(i+1))
lru_faults.append(lru(i+1))
fifo_faults.append(fifo(i+1))
GraphPlot.show_graph(opt_faults, lru_faults, fifo_faults)
print(opt_faults)
print(lru_faults)
print(fifo_faults)
print('Done.')
# -*- coding: utf-8 -*-
# @Time : 2020/3/26 00:42
# @Author : JeremyZhao1998
# @File : GraphPlot.py
# @Software : PyCharm
# @Description: To plot the graph of the result of the three algorithms
import matplotlib.pyplot as plt
x = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
def show_axis():
plt.xlim(0, 11)
plt.xticks([0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10])
plt.ylim(0, 100)
plt.yticks([0, 10, 20, 30, 40, 50, 60, 70, 80, 90, 100])
for i in range(10):
plt.plot([0, 11], [(i+1)*10, (i+1)*10], linewidth='1', color='aliceblue')
plt.plot([i+1, i+1], [0, 100], linewidth='1', color='aliceblue')
def show_graph(opt_faults, lru_faults, fifo_faults):
show_axis()
ln1, = plt.plot(x, opt_faults, color='cornflowerblue', marker='o', markersize='3')
ln2, = plt.plot(x, lru_faults, color='gold', marker='^', markersize='3')
ln3, = plt.plot(x, fifo_faults, color='firebrick', marker='D', markersize='3')
plt.legend([ln1, ln2, ln3], ['OPT', 'LRU', 'FIFO'])
for i in range(10):
plt.text(i + 1, opt_faults[i] + 1, str(opt_faults[i]), ha='center', va='bottom', fontsize='8')
plt.text(i + 1, lru_faults[i] + 1, str(lru_faults[i]), ha='center', va='bottom', fontsize='8')
plt.text(i + 1, fifo_faults[i] + 1, str(fifo_faults[i]), ha='center', va='bottom', fontsize='8')
plt.show()