SPSS探索分析实践操作

SPSS为我们提供了探索分析，所谓探索分析之所以是探索，是因为有时候我们对于变量的分布特点不是很清楚，探索的目的在于帮助我们完成以下的工作：

识别数据：例如数据的分布形式、异常值、缺失值；

正态性检验：服从正态分布的检验；

方差齐性检验：不同数据组的方差是否相等。

有关于方差齐性检验原理、正态分布这里不累述，这里主要介绍SPSS的探索分析使用。

数据文件

这里使用的文件是不同周期的充值用户的充值数据，这里主要是针对流失用户和活跃用户的充值数据。

具体操作

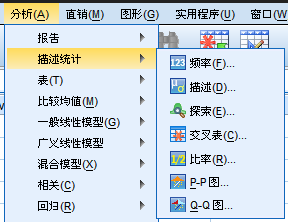
首先将源文件加载到SPSS中，选择菜单分析|描述统计|探索，如下图所示：

在该对话框中，有几个输入的位置：

因变量：为我们要分析的目标变量，变量多是连续性变量居多。

因子：是目标变量的分组，本例中，就是针对充值用户的充值金额进行分组，比如活跃和流失两组。

标注个案：对于异常值进行标注，识别异常值。

在此处，我们因变量选取充值总额，因子选取用户状态，标注个案我们选取服务器ID，如下图所示：

在该弹窗还有几个按钮，首先我们设置一下统计量按钮，打开统计量的窗口如下所示：

该弹窗的作用主要是设置输出时的统计量，在该弹窗可以看到以下的信息：

描述性：主要是完成输出一些我们之前说过的描述性统计的统计量，这些信息详见（http://www.cnblogs.com/yuyang-DataAnalysis/archive/2011/10/23/2221838.html）。同时这里还有一个置信区间的设置问题，这里默认的是95%，关于置信区间以后会说到，这里不再累述。

M-估计量：输出四种均值的稳健极大Ê���������������������里面有稳健估计量、非稳健估计量、波估计值、复权重估计量，有关于这部分的信息参见附件。

界外值：输出变量数据的前5个最大值和后5个最小值。

百分位数：变量数据的百分位数。

这里我们只选择描述性就可以了。接下来就是绘制对话框的设置了。

在此对话框中，有箱图、描述性、伸展与级别Levene检验三部分构成。首先来看箱图部分。

我们默认选择按因子水平分组，这标志着因变量的箱图将按照因子进行多个显示，此时就会有多个箱图，这取决于你分组的个数决定，当然不分组，就只会显示一个箱图，无，则就是不显示箱图。

描述性，则是选择输出的图形的种类而异。

伸展与级别Levene检验是设置数据转换的散步水平，其实���������������������据变化的设置。有完成两个任务，一个是数据转换后的回归曲线斜率，另一个就是方差齐性检验。该部分主要有四种选项，无、幂估计、已转换、未转换。

无，则是不输出，变量的散步水平；

未转换，不对原始数据进行变换；

已转换，对因变量进行数据转换，方法有自然对数变换、1/平方根变换、倒数变换、平方根变换、立方变换。

幂估计，对每一个变量数据产生一个中位数的自然对数和四分位数的自然对数的�����������������������的方差转化为同方差所需要的幂的估计。

在此处，我们选择无。

当然在这个对话框中，还有一个部分比较重要，那就是带检验的正态图。此选项能够输出正态概率图和离散概率图，且可以输出变量数据经Lilliefors显著水平修正的K-S和S-W的统计量。

下面就是选项对话框的设置了，该部分主要是针对缺失值的处理，方法有三种：

按列表排除个案：只要任何一个变量含有缺失值，就要踢出所有因变量或分���������������������amp;#20540;的观测记录。

按对排除个案：仅仅踢出所用到的变量的缺失值。

报告值：变量中存在缺失值单独作为一个类别进行统计，输出。

之后确定，结果输出，所有的结果会在查看器重显示，如下图：

报告分为几部分，摘要、描述统计、正态性检验、各种图形。

摘要部分

主要是确认是有缺失值情况信息。

描述统计部分

主要输出各项统计信息，参看描述性统计一文介绍。

正态性检验部分

Df表示自由度

Sig表示检验的显著水平，即P值，一般来说P值越大，越支持正态分布。

此处我们假设服从正态分布，根据K-S统计量和S-W统计量可以看出，两种用户的充值总额显著水平小于5%，即sig<0.05不服从正态分布。

图形部分

上图为茎叶图

Frequency表示数据的频数，ster��������������������示叶，两者表示数据的整数部分和小数部分，Stern width表示宽度。

怎么看这个茎叶图？

茎叶图其实是一种很形象的图示，下面告诉诸位怎么看茎叶图。简单的一句话解释就是：多少频数就代表多少（叶子+茎）。下面举一个例子来看。比如下图的数据：

其含义代表充值额2.5元的有���������������������40;额2.8有两例，共计5例。

此外还有标准和趋势QQ图,用于从图形的角度来分析数据是否呈现正态分布。

首先来看标准QQ图，如果服从正态分布，则散点分布是接近于一条直线的，形式如下：

然而在本类中，我们看到流失玩家和活跃玩家的充值金额QQ图如下：

可以看到是不符合正态分布的。同样的我们看到的趋势QQ图则也是要分布在直线周围才是正态分布，而在下面的趋势QQ图中，却不是这样的情况。

最后还有一个图，就是箱线图，有关箱线图的解释和分析，已经在以前的文章中有所阐述，可翻阅（http://www.cnblogs.com/yuyang-DataAnalysis/archive/2012/03/08/2385874.html）。

这里简单的再说一句，矩形框的部分是箱线图的主体，上中下三线代表75%，50%，25%的百分位数。

纵向的直线叫做触须线，上截止到变量本体的最大值，下截止到变量本体的最小值。所谓本体即除奇异值以外 的变量��������������������mp;#20540;。

奇异值，用0作为标记，分大小两种，箱体上方用0标记，变量值超过第75分位与25分位数的变量差的1.5倍。箱体下方则表示小于这个1.5倍。

极值，用*表示，箱体上方是超过变量差值的3倍（75分位和25分位之差），箱体下方同理。

按照上述的叙述，可以看看我们所分析的数据的具体情况，这里不再累述了。

以上结合了一些教材把探索性分析的基本操作讲述了一遍，作为探索性分析这只是我们作为更深入分析的一个前奏过程，但是这里却不能忽略其价值，比如怎么看茎叶图，箱线图，正态分布检验等等，在网游行业的应用其实也有很多，比如今天提到的不同生命周期玩家的充值的探索性分析，还有比如付费与非付费玩家的等级成长探索分析，不同服务器，不同渠道，不同充值平台之间的玩家的探索分析，这些虽然看似简单，但是都是值得去做和慢慢研究的。