数据挖掘导论课后习题答案-第六章
最近在读《Introduction to Data Mining 》这本书,发现课后答案只有英文版,于是打算结合自己的理解将答案翻译一下,其中难免有错误,欢迎大家指正和讨论。侵删。
第六章
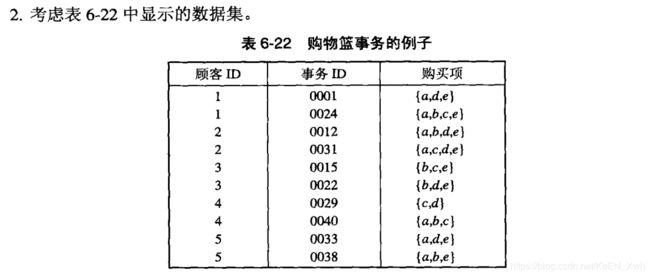


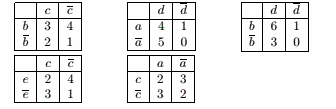
(a)Se = 8/10 = 0.8
Sbd = 2/10 = 0.2
Sbde = 2/10 = 0.2
(b)Cbd→e = 0.2/0.2 = 1
Ce→bd = 0.2/0.8 = 0.25
(c)Se = 4/5 = 0.8
Sbd = 5/5 = 1
Sbde = 4/5 = 0.8
(d)Cbd→e = 0.8/1 = 0.8
Ce→bd = 0.8/0.8 = 1
(e)没有明显的关系

![]()
(a)
CØ→A = SØ→A
CA→Ø = 100%
(b)
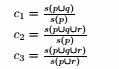
显然 c1 ≥ c2 ,c3 ≥c2
c2具有最低的置信度
(c)更正:假设B中的规则都有相同的支持度。
则c1 = c2 ≤ c3
c3具有最高的置信度
(d)举个反例:
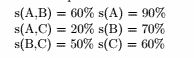
设minconf = 50%
cA→B = 66% > minconf
cB→C = 71% > minconf
cA→C = 22% < minconf

(a)是反单调的。
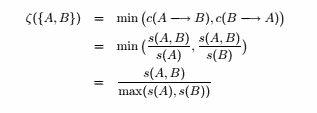
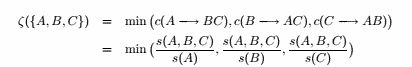
![]()
因为 s ( A , B , C ) ≤ s ( A , B ) 且 max ( s(A) , s(B) , s( C ) ) ≥ max ( s(A) , s(B) )
因此
![]()
(b)
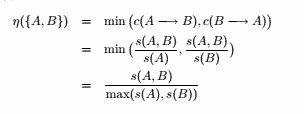
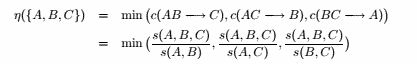
![]()
因为 s ( A , B , C ) ≤ s ( A , B ) 且 max ( s(A , B) , s(A , C) , s(B , C) ) ≤ max ( s(A) , s(B) )
因此是不单调的。
(c)
![]()

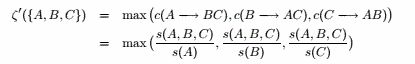
![]()
因为 s ( A , B , C ) ≤ s ( A , B ) 且 min ( s(A) , s(B) , s( C ) ) ≤ min ( s(A) , s(B) )
因此是不单调的。
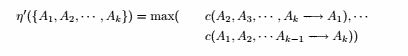

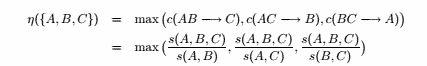
![]()
因为 s ( A , B , C ) ≤ s ( A , B ) 且 min ( s(A , B) , s(A , C) , s(B , C) ) ≤ min ( s(A) , s(B) , s( C ) ) ≤ min ( s(A) , s(B) )
因此是不单调的。

(a)
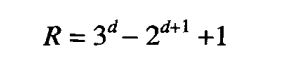
R = 37 - 28 + 1 = 602
(b)4
(c)C36 = 20
(d){ 面包,黄油 }
(e){ 啤酒,饼干 } ,{ 面包,黄油 }


(a)
{1,2,3,4}、{1,2,3,5}、{1,2,4,5}、{1,3,4,5}、{2,3,4,5}
(b)
{1,2,3,4}、{1,2,3,5}、{1,2,4,5}、{2,3,4,5}
(c)
{1,2,3,4}


(a)
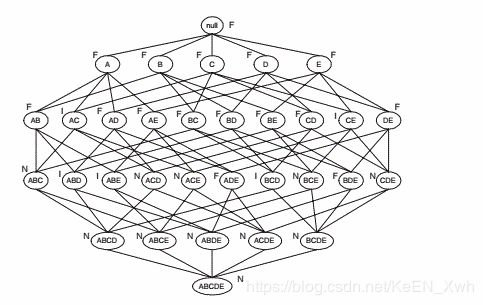
(b)16/32 = 50%
(c)11/32 = 34.4%
(d)5/32 = 15.6%
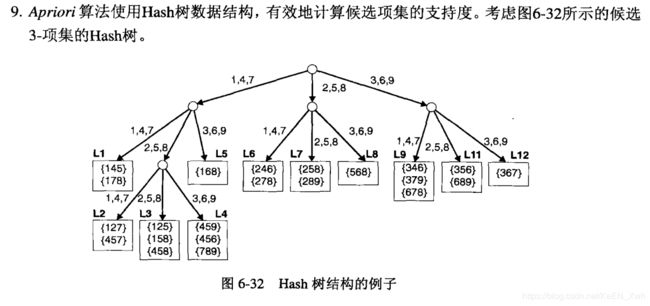

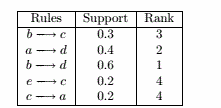
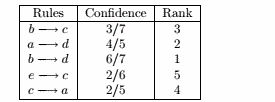
(a) L1 L3 L5 L9 L11
(b){ 1 4 5 } ,{ 1 5 8 } ,{ 4 5 8 }

(a)
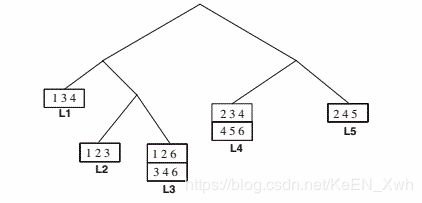
(b)5个叶结点和4个内部结点
(c)L1 L2 L3 L4,产生{ 1 2 3 } ,{ 1 2 6 }

![]()
解:


(a)
(b)
i.
ii.
iii.
iv.
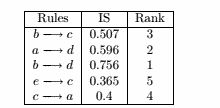
v.
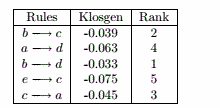
vi.
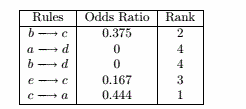


(a)e
(b)d不产生任何频繁项集
(c)a
(d)b
(e)e

(a)范围为0到1,当P ( B | A ) = 1 时取最大值,当 P ( B | A ) = P ( B ) 时取最小值
(b)M又可以写成:
![]()
因此M也增加
(c)M减小
(d)M减小
(e)不对称
(f)0
(g)不是
(h)会变
(i)不对称

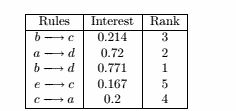
(a)c = 0.2/0.25 = 0.8
因此是有趣的
(b)I = 0.2 / ( 0.25 × 0.9 ) = 0.889
两项之间联系不大
(c)有高置信度的规则不一定有趣
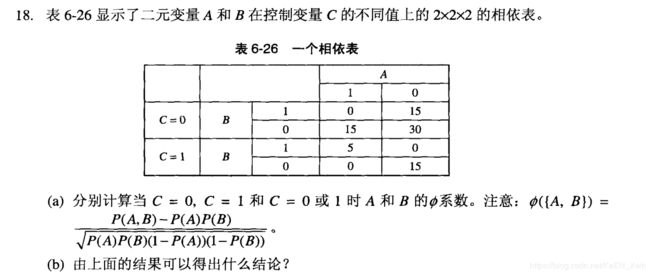
(a)
c = 0 : ( 0 - 1/4 × 1/4 ) / ( 1/4 × 1/4 × 3/4 × 3/4 )0.5 = -1/3
c = 1 : ( 1/4 - 1/4 × 1/4 ) / ( 1/4 × 1/4 × 3/4 × 3/4 )0.5 = 1
c = 0或1 : ( 1/16 - 1/4 × 1/4 ) / ( 1/4 × 1/4 × 3/4 × 3/4 )0.5 = 0
(b)如果不考虑分类因素的话某些有趣的结果会消失
![]()
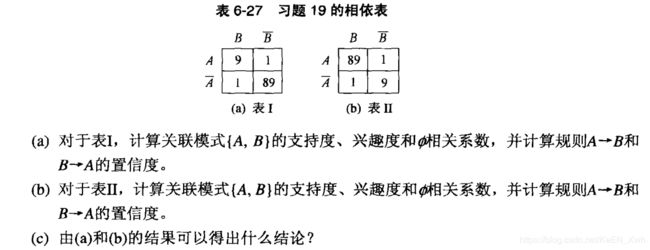

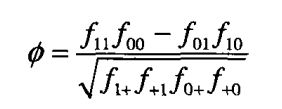
(a)
s(A) = 0.1 , s(B) = 0.9 , s(A , B) = 0.09
I ( A , B ) = 9 , Φ( A , B ) = 0.89 , c(A→B) = 0.9 , c(B→A) = 0.9
(b)
s(A) = 0.9 , s(B) = 0.9 , s(A , B) = 0.89
I ( A , B ) = 1.09 , Φ( A , B ) = 0.89 , c(A→B) = 0.98 , c(B→A) = 0.98
(c)
在反演操作下,只有Φ不变

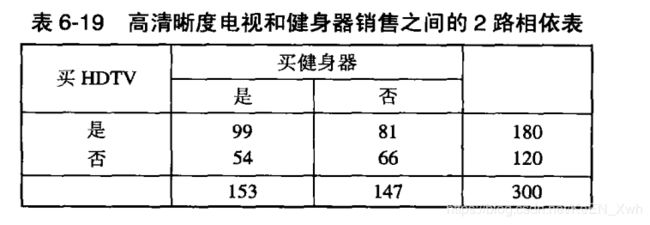
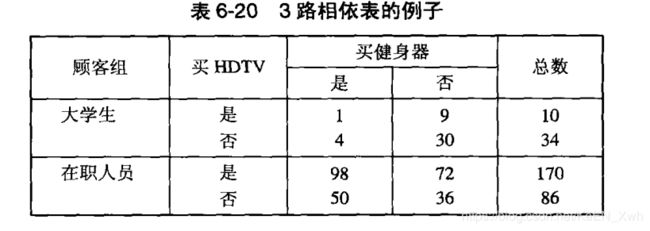
(a)
6.19 : α = ( 99 × 66 ) / ( 81 × 54 ) = 1.4938
6.20 : 大学生:α = ( 1 × 30 ) / ( 4 × 9 ) = 0.8333 在职人员:α = ( 98 × 36 ) / ( 72 × 50 ) = 0.98
(b)
6.19 : Φ = ( 300 × 99 - 180 × 153 ) / ( 153 × 147 × 180 × 120 )0.5 = 0.0980
6.20 : 大学生 : Φ = ( 44 × 1 - 10 × 5 ) / ( 10 × 5 × 39 × 34 )0.5 = -0.0233
在职人员 : Φ = ( 256 × 98 - 170 × 148 ) / ( 170 × 86 × 148 × 108 )0.5 = -0.0047
(c)
6.19 : I = ( 300 × 99 ) / ( 180 × 153 ) = 1.0784
6.20 : 大学生 : I = ( 44 × 1 ) / ( 10 × 5 ) = 0.88
在职人员 : I = ( 256 × 98 ) / ( 148 × 170 ) = 0.9971