基于信息增益的ID3决策树介绍。
这篇文章介绍一下一种常见的机器学习算法:决策树。这篇文章的主要是根据《机器学习》中的知识点汇总的,其中使用了《机器学习实战》的代码。关于决策树中基本信息以及公式更加推荐看一看《机器学习》这本书,书中不仅仅介绍了ID3决策树,而且还包含了C4.5以及CART决策树的介绍。所以本篇文章将使用西瓜书(也就是《机器学习》,以后都用西瓜书代替)中的数据集来进行测试。
决策树的介绍。
顾名思义,决策树这个名字可以分为两部分:决策和树。树的意思就是这个算法模型是以树状的形态进行表示的。而树的生成是和“决策”这一过程有关的。
那么决策是什么呢?
我们以二分类任务为例,以西瓜书数据集2.0作为测试数据,该数据最终会有两种不同的分类:好瓜和坏瓜。我们如果想要对一个西瓜进行分类,按照日常的思维就是买瓜的时候就会看看这个西瓜的外形是否正常,敲击西瓜听声音等等手段来判断这个瓜好不好,其实我们在判断的过程中就是一个“决策”的过程。
假如以数据集中的特征为例,来判断某个西瓜是不是好瓜我们该怎么做呢?
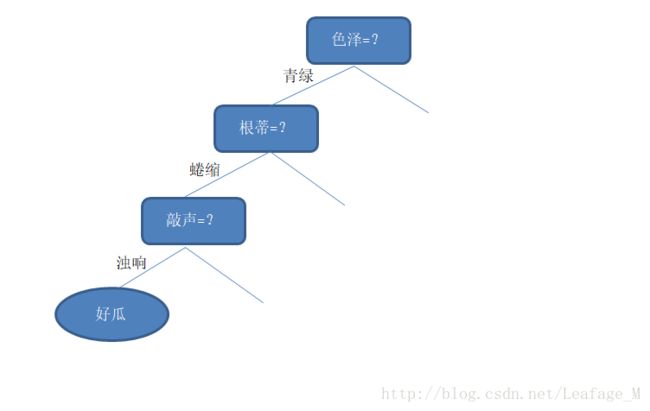
我们先看“它是什么颜色的?”,如果是“青绿色”,则我们再看“它的根蒂是什么形态的?”,如果是“蜷缩”,我们再判断“它敲起来是什么声音?”,最后,我们得出最终决策:这是个好瓜。
在这个过程中,我们在观察西瓜颜色、根蒂、敲击声的时候就已经在做“决策”了,但是这个决策只会在判断西瓜的过程中起到一部分的作用,所以这个时候的决策称为“子决策”,而我们通过这多个“子决策”共同决定出一个最终决策:这是个好瓜。
将上述过程图形话就如下所示:
可以从图中能够大概看出是一个树状的图形,其中没有绘出的节点就是一些其他的情况,比如色泽等于浅白、乌黑等。
显然,决策过程的最终结论对应了我们所希望的判定结果,例如“是”或者“不是”好瓜;决策过程中提出的每个判定问题都是对某个属性的“测试”,例如“色泽=?”“根蒂=?”;每个测试的结果或是导出最终结论,或是导出进一步的判定问题,其考虑范围都是在上次决策结果的限定范围之内,例如若在“色泽=青绿”之后再判断“根蒂=?”,则仅再考虑青色瓜的根蒂,而不再考虑其他颜色的西瓜。
所以一个决策树可以分为以下几点进行表示:
- 一般的,一颗决策树包含一个根节点、若干个内部节点和若干个叶节点;
- 叶节点对应决策结果(比如说好瓜或者坏瓜);其他每个节点则对应于一个属性测试(也就是根据某个特征做出的判断,比如“根蒂=?”就是在数据集上对根蒂进行判断测试);
- 每个节点包含的样本集合根据属性测试的结果被划分到子节点中(也就是说如果某个特征相同的特征值划分到同一个子节点中,比如“根蒂=蜷缩”,我们就把根蒂这个特征中特征值等于蜷缩的全部划分到一起(当然,需要满足上面一个特征的测试,也就是当前的色泽=青绿))
- 根节点包含样本全集,根节点的时候还没有进行划分,所以包含样本全集。
划分选择。
我们从上面就能够看出,决策树的整个流程主要就是依赖根据特征所做出的“决策”,从而将样本及划分到下一个节点中去。
那么毫无疑问,决策树的关键点就是如何选择最优划分属性,也就是说西瓜中共有:色泽、根蒂、敲声、纹理、脐部、触感这么多的特征属性,我们优先根据哪一个特征去进行划分呢?
一般而言,随着划分过程的不断进行,我们希望决策树的分支节点所包含的样本尽可能属于同一类别,即节点的“纯度”越来越高。
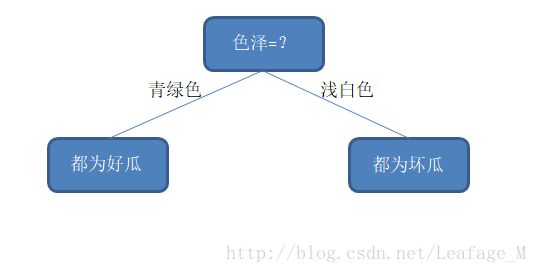
假设,按照色泽来划分的话,划分完成之后整个西瓜样本集正好被分为两类了,一类全部都是好瓜,另一类全部都是坏瓜,那么在两个分支的纯度都是百分之百了。
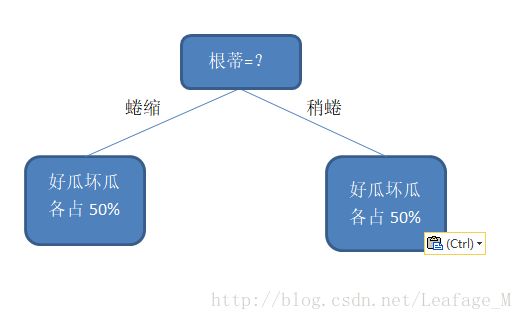
但是,如果我们按照根蒂来划分的话,划分完成之后,两个分支里面好瓜和坏瓜都是各占50%,那么这两个分支的纯度就是百分之五十,那么我们就需要继续选取特征继续划分。
很显然,上述中选取“色泽”这个特征来划分更好一点,因为这样划分完的纯度最高(纯度的计算并不是这样的,这里只是为了能够更好的理解“纯度”这个概念才这样计算的)。
那么究竟如何在众多特征中,选取一个特征来进行划分使得各个分支的纯度最大呢?
注:
根据不同的划分方法,决策树就被分为好几种类型,如果使用”信息增益“的方法进行划分,这样的决策树称为ID3决策树,如果使用”增益率“来划分,这样的决策树称为C4.5决策树,如果使用“基尼指数”来划分,这样的决策树称为CART决策树,下面介绍一下“信息增益”的划分方法。
信息熵。
那么问题就来到了“纯度”的计算,通过什么样的算法得到的各个分支纯度最大是现在的问题所在。
这里就引入了“信息熵”这个概念,信息熵是度量样本集合纯度最常用的一种指标。(这里的信息熵是克劳德·艾尔伍德·香农提出的,在《数学之美》中有过这段内容:记得有个国外的学者说过,人们通常把香农与爱因斯坦,牛顿相提并论,这是不公平的—-对香农是不公平的。香农为现代信息革命打下了理论基础)
下面就进入到了如何计算“信息熵”的阶段,首先信息熵的定义为如下:
假定当前样本集合D中第k类样本所占的比例为 pk ( k =1,2,…,| y |(注意这里的k为下标)),则D的信息熵定义为:
注:在Word中按下[Alt]+[=]即可编辑公式。
而且 Ent(D) 的值越小,则D的纯度越高。
我们来根据西瓜数据集2.0(数据集可见:西瓜数据集)计算一下信息熵:
在该数据集中,一共包含17个训练样例,因为数据集中的分类结果只有好瓜和坏瓜两种。所以与上述的信息熵描述对应的就是:这17个训练样例就是样本集合D,集合中共有好瓜和坏瓜,那么集合一共只有两类,所以| y |=2,自然k的取值为1和2。
所以在决策树开始之前,根节点是包含所有的样本集也就是17个样本,其中好瓜的比例为: p1=817 ,那么坏瓜的比例为: p2=917 ,那么套入信息熵公式中:
这样就能够算出根节点的信息熵了,显然这个信息熵很大,所以这个时候根节点的纯度并不高(再次提醒, Ent(D) 越小,D 的纯度越高。)
同时,计算信息熵时约定:若 p =0,则 plog2p=0 。
并且 Ent(D) 的最小值为0,最大值为 log2|y| 。
这个也很好证明:
最小值证明:
当样本中只有一种分类,那么 p1=1 ,带入公式中 log21=0 ,所以计算得到的 Ent(D)=0 ,此时纯度最高,即样本集中只有一个分类。最大值证明:
当集合中 D 共有 y 个分类,并且样本的分类所占的比重都一样,那么 p1=p2=...=py=1y ,那么可推出 Ent(D)=−log21y=−log2y−1=log2y 。这里的 y 显然为正,所以多一个绝对值符号也无妨。而此时显然纯度最低,毕竟每个分类所占的比重都一样,比较混杂。
这样我们就能够通过计算信息熵的方法,将当前节点样本中的“纯度”计算出来。既然信息熵越小纯度越高,那么我们的目标就是通过属性的划分,让子类中的信息熵变得越来越小。
信息增益。
如何选取特征进行划分,从而让子类中的信息熵变得越来越小呢?这里就引入了“信息增益”这个概念。
首先看一下“信息增益”的概念和计算过程:
假定离散属性 a 有 V 个可能取的值{ a1,a2,...,aV },若使用 a 来对样本集 D 进行划分,则会产生 V 个分支节点,其中第 v 个分支节点包含了 D 中所有在属性 a 上取值为 av 的样本,记为 Dv 。我们可以根据上述的信息熵计算公式,计算出 Dv 的信息熵,再考虑到不同的分支节点所包含的样本数不同,给分支赋予权重 |Dv||D| ,即样本数越多分支节点的影响值越大,于是可计算出属性 a 对样本集 D 进行划分所获得的“信息增益”。
信息增益计算公式: Gain(D,a)=Ent(D)−∑Vv=1|Dv||D|Ent(Dv)
一般而言,信息增益越大,则意味着使用属性 a 来进行划分所获得的“纯度提升”越大。这是为什么呢?
道理其实也很简单:从上述的信息增益计算公式中能够看出, Ent(D) 的值在当前节点中是一个固定值,比如我们刚才计算出来的0.998。那么 Gain(D,a) 的值就跟后面的 ∑Vv=1|Dv||D|Ent(Dv) 有关,这个值越小,信息增益最后计算得到的值就越大。而这个值越小,就代表着其中的 Ent(Dv) 越小就说明分支中的信息熵越小(这里的权重仅代表着分支节点的影响,所以我们可以先假设各个分支影响值一样,那么就只跟 Ent(Dv) 有关了),信息熵越小也就代表着“纯度”越高,那么这显然就是我们想要的结果。
所以我们的最终目标就已经明确了,计算各个属性的信息增益,找出信息增益最大的那个属性作为我们的划分点,这样决策树的分支节点的纯度就会越来越高。
计算信息增益 。
如果将上述的“信息增益”应用到西瓜数据集中,我们选取“色泽”这个属性讲解,那么对应的内容应该是这样的:
全部的西瓜数据集 D 一共有17个样本,其中有色泽这个属性(对应上述的 a ),在色泽中一共有三种(对应上述的 V )可能取的值 {青绿,浅白,乌黑},如果我们使用色泽这一属性对全部的样本集 D 进行划分的话,那么一共会产生三个分支(这三个分支在上述中对应的就是 v ),分别是{ D青绿,D浅白,D乌黑 }。
其中 D青绿 共有6个样本,这6个样本的色泽全部为青绿,所占总样本的比例为: 617 ;
其中 D浅白 共有5个样本,这5个样本的色泽全部为浅白,所占总样本的比例为: 517 ;
其中 D乌黑 共有6个样本,这6个样本的色泽全部为乌黑,所占总样本的比例为: 617 ;
(所占的比例对应的就是上述中的权重 |Dv||D| )
按照“信息增益”的公式,我们需要知道 Ent(D) 的值,这个值在上述已经计算过:
即: Ent(D)=0.998
其次,我们也已经计算出了各个分支的权重 |Dv||D|
即: D青绿=617 、 D浅白=517 、 D乌黑=617
那么我们就只需要计算各个分支的 Ent(Dv) :
首先来计算 Ent(D青绿) ,在分支样本集 D青绿 共有6条数据,其数据如下:
| 编号 | 色泽 | 根蒂 | 敲声 | 纹理 | 脐部 | 触感 | 好瓜 |
|---|---|---|---|---|---|---|---|
| 1 | 青绿 | 蜷缩 | 浊响 | 清晰 | 凹陷 | 硬滑 | 是 |
| 4 | 青绿 | 蜷缩 | 沉闷 | 清晰 | 凹陷 | 硬滑 | 是 |
| 6 | 青绿 | 稍蜷 | 浊响 | 清晰 | 稍凹 | 软粘 | 是 |
| 10 | 青绿 | 硬挺 | 清脆 | 清晰 | 平坦 | 软粘 | 否 |
| 13 | 青绿 | 稍蜷 | 浊响 | 稍糊 | 凹陷 | 硬滑 | 否 |
| 17 | 青绿 | 蜷缩 | 沉闷 | 稍糊 | 稍凹 | 硬滑 | 否 |
按照信息熵的公式: Ent(D)=−∑|y|k=1pklog2pk 。
从数据表中可知共有两种分类,其中好瓜的比例为 36 ,坏瓜的比例也为 36 ,可以使用 p1 来标记好瓜的比例,使用 p2 来标记坏瓜的比例,所以 p1=p2=36 ,带入公式中得到: Ent(D青绿)=−(36log236+36log236)=1.000 ,其实这个就是当前 Ent(D) 的最大值了,说明此时纯度最低,各个分类所占比重一样,无法做出更好的判断。
继续计算 Ent(D浅白) ,在分支样本集 D浅白 共有5条数据,其数据如下:
| 编号 | 色泽 | 根蒂 | 敲声 | 纹理 | 脐部 | 触感 | 好瓜 |
|---|---|---|---|---|---|---|---|
| 5 | 浅白 | 蜷缩 | 浊响 | 清晰 | 凹陷 | 硬滑 | 是 |
| 11 | 浅白 | 硬挺 | 清脆 | 模糊 | 平坦 | 硬滑 | 否 |
| 12 | 浅白 | 蜷缩 | 浊响 | 模糊 | 平坦 | 软粘 | 否 |
| 14 | 浅白 | 稍蜷 | 沉闷 | 稍糊 | 凹陷 | 硬滑 | 否 |
| 16 | 浅白 | 蜷缩 | 浊响 | 模糊 | 平坦 | 硬滑 | 否 |
从数据表中得到 p1=15 、 p2=45 ,带入公式得: Ent(D浅白)=−(15log215+45log245)=0.722 ,可以看出这个值就小一点,对应的“纯度”就高,从表中也能够看出”纯度“高,因为此时大多出都为坏瓜,也算比较”纯“了。
最后计算 Ent(D乌黑) ,在分支样本集 D乌黑 共有6条数据,其数据如下:
| 编号 | 色泽 | 根蒂 | 敲声 | 纹理 | 脐部 | 触感 | 好瓜 |
|---|---|---|---|---|---|---|---|
| 2 | 乌黑 | 蜷缩 | 沉闷 | 清晰 | 凹陷 | 硬滑 | 是 |
| 3 | 乌黑 | 蜷缩 | 浊响 | 清晰 | 凹陷 | 硬滑 | 是 |
| 7 | 乌黑 | 稍蜷 | 浊响 | 稍糊 | 稍凹 | 软粘 | 是 |
| 8 | 乌黑 | 稍蜷 | 浊响 | 清晰 | 稍凹 | 硬滑 | 是 |
| 9 | 乌黑 | 稍蜷 | 沉闷 | 稍糊 | 稍凹 | 硬滑 | 否 |
| 15 | 乌黑 | 稍蜷 | 浊响 | 清晰 | 稍凹 | 软粘 | 否 |
从数据表中得 p1=46 、 p2=26 ,带入公式得: Ent(D青绿)=−(46log246+26log226)=0.918 ,这个”纯度“也是比较低的,能够从表中看出各个类别所占比例差得不太多。
那么我们得到了所有想要的数值,将它们全部带入到”信息增益“的公式中:
Gain(D,色泽)=Ent(D)−∑3v=1|Dv||D|Ent(Dv)=0.998−(D青绿D×Ent(D青绿)+D浅白D×Ent(D浅白)+D乌黑D×Ent(D乌黑))=0.998−(617×1.000+517×0.722+617×0.918)=0.109
这样我们就计算出了”色泽“的信息增益,我们可以使用同样的方法计算出其他属性的信息增益值:
Gain(D,根蒂)=0.143 ; Gain(D,敲声)=0.141 ; Gain(D,纹理)=0.381 ; Gain(D,脐部)=0.289 ; Gain(D,触感)=0.006 ;
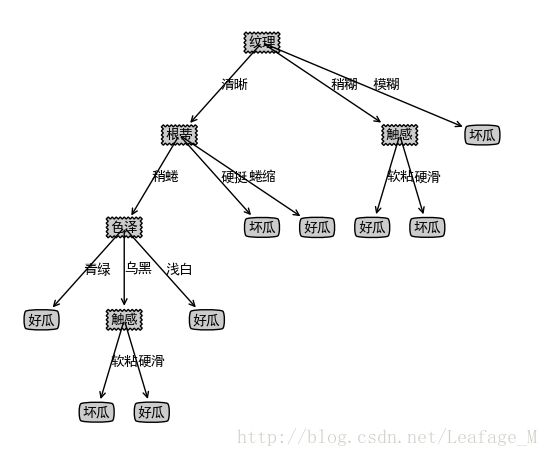
显然,属性”纹理“的信息增益量最大,说明如何按照”纹理“这个属性进行划分的话,分支节点的纯度比较高,于是它被选为划分属性。如果按照”纹理“这一属性对根节点进行划分的话,各分支节点包含的样本子集如下图所示,其中数字代表样本编号:
这样,我们就完成了第一次划分,按照纹理划分之后我们还需要继续划分,以图中的第一个子节点,即 {”纹理“ = ”清晰“}为例,该节点包含的样例 D1 一共有9个样例,此时可用的属性集合为{色泽,根蒂,敲声,脐部,触感},因为”纹理“的属性已经使用过了,所以不能够再次使用了,然后我们即可根据上述条件基于 D1 再次计算出各个属性的信息信息增益:
Gain(D,根蒂)=0.458 ; Gain(D,敲声)=0.331 ; Gain(D,脐部)=0.458 ; Gain(D,触感)=458 ;
在这里根蒂、脐部、触感三个属性均取得了最大的信息增益,可任取其中之一作为划分属性,再次划分得到子分支。
就这样不断的划分,直到遇到终止条件:
- 当前节点包含的样本全属于同一类别,无需划分;
- 当前属性集为空,或是所有样本再所有属性上取值相同,无法划分;
- 当前节点集合包含的样本集合为空,不能划分。
在第2种情形下,我们把当前节点标记为叶节点,并将其类别设定为该节点所含样本最多的类别;
在第3种情形下,同样把当前节点标记为叶节点,但将其类别设定为其父节点所含样本最多的类别。
注意这两种情形的处理实质不同:情形2实在利用当前节点的后验分布,而情形3是把父节点的样本作为当前节点的先验分布。
总结。
决策树基本知识都进行了介绍,这里选取信息增益作为划分特征的选择,当然也如文中所提到的”增益率“、”基尼指数“等,还有其它方法能够使用。
决策树使用起来效率不错,而且实现起来也不太难,算法的原理也比较理解,可谓是一个经久不衰的模型了。
在本文中并没有提及代码的实现,但是相关的代码已经实现,可以在本人的github中进行查看,传送门:西瓜书决策树实现
代码绘图结果: