FE离群点分析+分布分析
离群点
单变量分析
首先用标准化(标准化不会改变数据相对分布的特性)把数据转变成正态分布,分别查看最大和最小的十个值
saleprice_scaled = StandardScaler().fit_transform(df_train['SalePrice'][:,np.newaxis]);
low_range = saleprice_scaled[saleprice_scaled[:,0].argsort()][:10]
high_range= saleprice_scaled[saleprice_scaled[:,0].argsort()][-10:]
print('outer range (low) of the distribution:')
print(low_range)
print('\nouter range (high) of the distribution:')
print(high_range)
输出
outer range (low) of the distribution:
[[-1.83820775]
[-1.83303414]
[-1.80044422]
[-1.78282123]
[-1.77400974]
[-1.62295562]
[-1.6166617 ]
[-1.58519209]
[-1.58519209]
[-1.57269236]]
outer range (high) of the distribution:
[[ 3.82758058]
[ 4.0395221 ]
[ 4.49473628]
[ 4.70872962]
[ 4.728631 ]
[ 5.06034585]
[ 5.42191907]
[ 5.58987866]
[ 7.10041987]
[ 7.22629831]]
可以发现,Low range值偏离原点并且都比较相近,High range离远点较远,7.很可能是异常值
双变量分析
以GrLivArea为X轴,SalePrice为y轴画散点图
var = 'GrLivArea'
data = pd.concat([df_train['SalePrice'], df_train[var]], axis=1)
data.plot.scatter(x=var, y='SalePrice', ylim=(0,800000));
从图中看出二者很可能有线性关系,则图中右下方的两个点作为异常值舍弃
df_train.sort_values(by = 'GrLivArea', ascending = False)[:2]
df_train = df_train.drop(df_train[df_train['Id'] == 1299].index)
df_train = df_train.drop(df_train[df_train['Id'] == 524].index)
---------------------
散点图
#单列散点图
ax = sns.scatterplot(x="isFraud", y="id_01", data=train)
#多列散点图
sns.set()
cols = ['SalePrice', 'OverallQual', 'GrLivArea', 'GarageCars', 'TotalBsmtSF', 'FullBath', 'YearBuilt']
sns.pairplot(df_train[cols], size = 2.5)
plt.show();
分布
热图
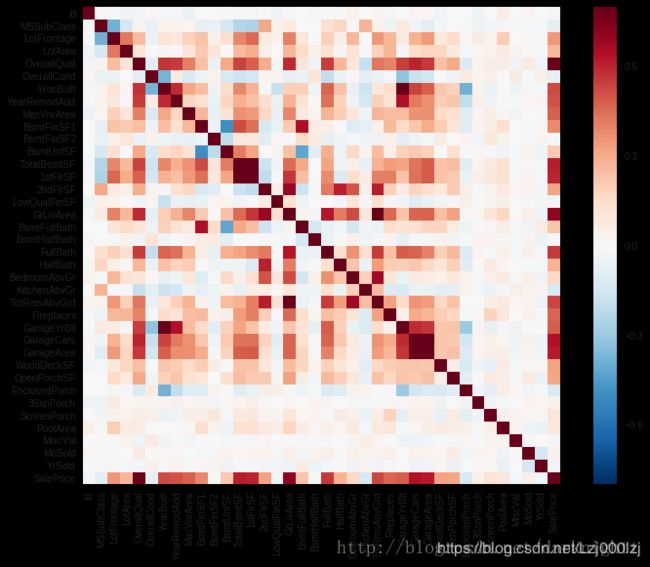
#简单的热图
corrmat = df_train.corr()
f, ax = plt.subplots(figsize=(12, 9))
sns.heatmap(corrmat, vmax=.8, square=True);
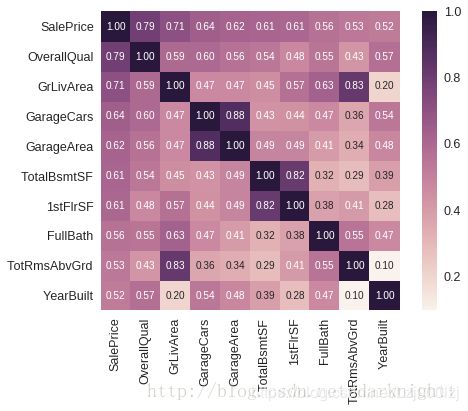
#选取与SalePrice相关系数最高的10个特征作热图,显示相关系数
k = 10 #number of variables for heatmap
cols = corrmat.nlargest(k, 'SalePrice')['SalePrice'].index
cm = np.corrcoef(df_train[cols].values.T)
sns.set(font_scale=1.25)
hm = sns.heatmap(cm, cbar=True, annot=True, square=True, fmt='.2f', annot_kws={'size': 10}, yticklabels=cols.values, xticklabels=cols.values)
plt.show()
检验正太分布
scipy库中stats对象的.probplot() 方法拟合一个高斯正态分布,注意:这里要求列不能包含空值。
sns.distplot(df_train['SalePrice'], fit=norm);
fig = plt.figure()
res = stats.probplot(df_train['SalePrice'], plot=plt)

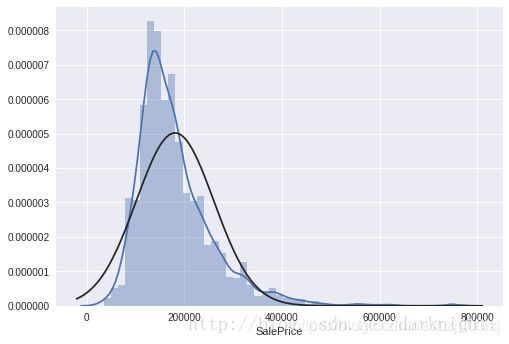
看到数据呈正偏态分布,现在我们想把它转变成正太分布。统计学里面一个常用的做法就是对SalePrice的取log。
df_train['SalePrice'] = np.log(df_train['SalePrice'])
sns.distplot(df_train['SalePrice'], fit=norm);
fig = plt.figure()
res = stats.probplot(df_train['SalePrice'], plot=plt)
对SalePrice做了log变换之后近似于正态分布了
但是由于上面的方法不适用于带空值的列,可以用skew,kurt来判断是否为正太分布
print("Skewness: %f" % train['id_01'].skew())
print("Kurtosis: %f" % train['id_01'].kurt())
- 偏度(Skewness)用来描述数据分布的对称性,正态分布的偏度为0。计算数据样本的偏度,当偏度<0时,称为负偏,数据出现左侧长尾;当偏度>0时,称为正偏,数据出现右侧长尾;当偏度为0时,表示数据相对均匀的分布在平均值两侧,不一定是绝对的对称分布,此时要与正态分布偏度为0的情况进行区分。当偏度绝对值过大时,长尾的一侧出现极端值的可能
- 峰度(Kurtosis)用来描述数据分布陡峭或是平滑的情况。正态分布的峰度为3,峰度越大,代表分布越陡峭,尾部越厚;峰度越小,分布越平滑。很多情况下,为方便计算,将峰度值-3,因此正态分布的峰度变为0,方便比较。在方差相同的情况下,峰度越大,存在极端值的可能性越高。
缺失部分的数数据的可视化
train_null = (train.isnull().sum() / len(train)) * 100
train_null = train_null.drop(train_null[train_null == 0].index).sort_values(ascending=False)[:50]
missing_data = pd.DataFrame({'Missing Ratio' :train_null})
f, ax = plt.subplots(figsize=(15, 12))
plt.xticks(rotation='90')
sns.barplot(x=train_null.index, y=train_null)
plt.xlabel('Features', fontsize=15)
plt.ylabel('Percent of missing values', fontsize=15)