Non-delusional Q-learning and Value Iteration笔记

Non-delusional Q-learning and Value Iteration

1. 论文讲了什么/主要贡献是什么

文章发现了Q-learning和带有函数逼近或其它策略约束的近似动态规划中存在错觉偏差的问题，并且对错觉偏差进行了定义。发现了一个可以提升算法性能的方式。并且文中开发了一种新的策略类一致性备份操作符，以及相应的基于模型的PCVI和无模型的PCQL算法，这些算法完全消除了错觉偏差。

错觉偏差：在进行策略选择和值函数更新时，每步都采用了贪婪策略，选择了值函数最大对应的动作，但在一个策略下可能无法完成采用贪婪策略所选择的动作序列，因此在更新过程中的值函数与实际可达到的最优值函数也是存在偏差的。

2. 论文摘要：

We identify a fundamental source of error in Q-learning and other forms of dynamic programming with function approximation. Delusional bias arises when the approximation architecture limits the class of expressible greedy policies. Since standard Q-updates make globally uncoordinated action choices with respect to the expressible policy class, inconsistent or even conflicting Q-value estimates can result, leading to pathological behaviour such as over/under-estimation, instability and even divergence. To solve this problem, we introduce a new notion of policy consistency and define a local backup process that ensures global consistency through the use of information sets—sets that record constraints on policies consistent with backed-up Q-values. We prove that both the model-based and model-free algorithms using this backup remove delusional bias, yielding the first known algorithms that guarantee optimal results under general conditions. These algorithms furthermore only require polynomially many information sets (from a potentially exponential support). Finally, we suggest other practical heuristics for value-iteration and Q-learning that attempt to reduce delusional bias.

我们确定了Q-learning和其他形式的带有函数近似的动态规划的基本误差来源。当近似结构限制了可表达的贪婪策略的类别时，产生了错觉性偏差。由于标准的Q-updates对可表达的策略类做出全局不协调的行动选择，可能导致不一致甚至相互冲突的Q值估计，导致过度/低估、不稳定甚至发散等病态行为。为了解决这个问题，我们引入了一个新的策略一致性概念，并定义了一个本地备份过程，该过程通过使用信息集来确保全局一致性——这些信息集记录与备份的Q值一致的策略约束。我们证明使用这种备份的基于模型和无模型的算法都消除了错觉偏差，成为了在一般条件下保证最优结果的第一个已知算法。这些算法进一步只需要多项式多的信息集(来自潜在的指数支持)。最后，我们建议其他实用的启发式的价值迭代和Q-learning，试图减少错觉偏差。

3. 论文主要观点：

3.1 背景：

Q-learning的方法能够收敛到一个最优的状态-动作值函数，但是在使用函数逼近器，即使是简单的线性函数逼近器也会带来潜在的不稳定问题。目前有很多方法在调整更新方式、限制逼近器以及限制训练方法方面保证收敛性或提高逼近器表现。但是简单的调整可能无法保证达到最优表现，因为判断一个逼近器是否可以在最坏Bellman错误情况下有最小的误差是一个NP完全难题。因此设计一个Q-learning的具有好的最坏情况下的行为的变体仍然是一个问题。

3.2 问题：

Q-learning存在错觉偏差的问题。因为更新过程是基于相互不一致的值。出现这种不一致是因为Q更新是根据下一状态所有动作估计的最大值进行的，忽略了在逼近器中获得的可接受策略下无法实现选定动作的问题。这些“无约束”的更新会在目标值中产生错误，并导致不同的价值估计错误:Q-learning很容易根据贪婪策略类无法实现的操作选择来备份值。

3.3 方法：

首先说明一些符号表示， $\mathcal{F}=\left\{f_{\theta }:S\times A\to \mathbb{R}|\theta \in \Theta \right\}$表示可表示值函数逼近器集合，将可容许贪婪策略类表示为：
$$G(\Theta )=\left\{{\pi }_{\theta }|{\pi }_{\theta }(s)=\underset{a\in A}{\mathrm{argmax}}{f}_{\theta }(s,a),\theta \in \Theta \right\}$$
因此在线Q-learning在样本$s,a,r,s^{\prime }$ 处的更新为：
$$\theta \leftarrow \theta +\alpha \left(r+\gamma \underset{a^{\prime }\in A}{\max }{Q}_{\theta }\left(s^{\prime },a^{\prime }\right)-Q_{\theta }(s,a)\right){\nabla }_{\theta }{Q}_{\theta }(s,a)$$
其中$Q_{\theta }\in \mathcal{F}$。

下面介绍错觉偏差和错觉偏差造成的后果。

错觉偏差：每当从底层策略类中无法实现的操作选择派生出备份的值估计时，就会发生错觉性偏差。

在Q值更新的过程中，每个状态-动作对$(s,a)$的值是通过独立地选择在相应下一状态$s^{\prime }$下的动作获得。而动作的选择是根据值最大化操作，即取最大值。这个更新过程也就默认了一个假设：${\max }_{a^{\prime }\in A}{Q}_{\theta }\left(s^{\prime },a^{\prime }\right)$是可以实现的。但是如果在可容许类中没有一种策略可以将整个选择的动作序列表示出，这个备份值无法与任何可表示策略能够实现的Q值对应，此时的更新就会具有不一致性（与可表示策略不一致）。

图一 MDP

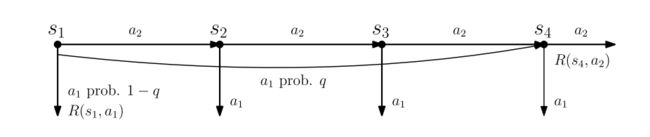
错觉偏差在Q值更新的过程会带来的问题有：Divergence、The Discounting Paradox、Approximate Dynamic Programming、Batch Q-learning。

文中的方法通过使用信息集来跟踪所有Q值中包含的“依赖项”，从而避免了错觉。例如，满足这个Q值所需要的策略假设。然后，备份会删除那些信息集与策略类不一致的不可行的值。由于在添加新依赖项时，备份的值可能被指定为不一致的，因此这种策略一致的备份必须维护备选信息集及其相应的Q值，从而允许(隐式)回溯以前的决策(例如最大q值选择)。这种策略一致的备份可以被看作是统一了基于值和策略的RL方法，

策略类值迭代

我们首先定义policy-class value iteration (PCVI)，这是一种新的VI方法，它对信息集集合进行操作，以确保在给定的类中发现最优策略。

策略类Q-learning

可以把PCQL看作是基于值和基于策略的RL的统一。带有函数逼近器的基于值的强化学习的目标是找到一个具有低贝尔曼错误（Bellman error, BE）的近似值函数或Q方程。这种强调小BE的一个原因是BE的最大范数可以用来直接限制由近似的VF/QF和最优策略的值所引起的贪婪策略值的(最大范数)损失。但是，使用BE近似值对诱导的策略质量的限制非常宽松。最小化BE无法提供实际的策略保证。一个小的BE实际上可能对所诱导的政策质量产生相当大的误导。例如，Q-learning使用最小二乘来最小化TD-error作为BE的代理，常常会产生质量较差的策略。

PCQL和PCVI将贝尔曼备份中无法通过可执行策略实现的值去掉。这样会导致比较大的BE错误，因为有些比较大的贝尔曼备份值被删掉。但是，这同时也保证了所产生的策略是可执行的，并且在可执行策略中是最优的。这样的回归过程可以看作是一个在可执行策略类中最优化值函数，使函数向着具有策略一致性的值迭代更新。

在文中的方法中，使用了信息集，这个信息集枚举了所有具有一致性的策略，而最终获得的策略一定是在信息集中的。用这种方法进行了策略搜索。这与其他的策咯搜索方法不同（如策略迭代），这个方法是直接通过使用贝尔曼备份值来直接进行策略搜索，保留具有一致性的贝尔曼备份值，保证了贝尔曼备份值都是能够实现的。

3.4 结论：

文章中定义了错觉偏差，这是Q-learning和带有函数逼近或其它策略约束的近似动态规划中的一个基本问题。错觉以不同的方式表现出来，导致近似质量差或发散的原因完全独立于近似误差本身。因此在Q-learning中错觉偏差是一个重要的风险因素。文章开发并分析了一种新的策略类一致性备份操作符，以及相应的基于模型的PCVI和无模型的PCQL算法，这些算法完全消除了错觉偏差。文章还提出了在实际大规模应用中可以减小错觉偏差的启发式方法。