LeetCode 1419. Minimum Number of Frogs Croaking
[Med] LeetCode 1419. Minimum Number of Frogs Croaking
链接: https://leetcode.com/problems/minimum-number-of-frogs-croaking/
题目描述:
Given the string croakOfFrogs, which represents a combination of the string “croak” from different frogs, that is, multiple frogs can croak at the same time, so multiple “croak” are mixed. Return the minimum number of different frogs to finish all the croak in the given string.
A valid “croak” means a frog is printing 5 letters ‘c’, ’r’, ’o’, ’a’, ’k’ sequentially. The frogs have to print all five letters to finish a croak. If the given string is not a combination of valid “croak” return -1.
给你一个字符串 croakOfFrogs,它表示不同青蛙发出的蛙鸣声(字符串 “croak” )的组合。由于同一时间可以有多只青蛙呱呱作响,所以 croakOfFrogs 中会混合多个 “croak” 。请你返回模拟字符串中所有蛙鸣所需不同青蛙的最少数目。
注意:要想发出蛙鸣 “croak”,青蛙必须 依序 输出 ‘c’, ’r’, ’o’, ’a’, ’k’ 这 5 个字母。如果没有输出全部五个字母,那么它就不会发出声音。
如果字符串 croakOfFrogs 不是由若干有效的 “croak” 字符混合而成,请返回 -1 。
Example 1:
Input: croakOfFrogs = “croakcroak”
Output: 1
Explanation: One frog yelling “croak” twice.
Example 2:
Input: croakOfFrogs = “crcoakroak”
Output: 2
Explanation: The minimum number of frogs is two.
The first frog could yell “crcoakroak”.
The second frog could yell later “crcoakroak”.
Example 3:
Input: croakOfFrogs = “croakcrook”
Output: -1
Explanation: The given string is an invalid combination of “croak” from different frogs.
Example 4:
Input: croakOfFrogs = “croakcroa”
Output: -1
Constraints:
- 1 <= croakOfFrogs.length <= 10^5
- All characters in the string are: ‘c’, ‘r’, ‘o’, ‘a’ or ‘k’.
Tag: String
解题思路
这道题目很有意思,我抽象一下这个题目的意思。一个字符串当中可能有多个 字符串"croak"按照掺杂在一起。题目让我们输出个数最少的,可以完成这个input string叫声的青蛙。比如说例子2当中,两个croak是混在一起的,所以必须由两个青蛙来完成。但是假设在第一声"croak"结束之后,也就是"crcoak|roak"在这个隔断的地方,后面又出现了一声"croak",假设添加在原字符串之后是"crcoak|(croak)roak",那么最优的情况下就是让第一个青蛙再叫一次就好了,而不是再添加一只青蛙。
这道题目有两个难点。第一个是我们需要判断所有的叫声是不是有效的。比如说例子三和例子四当中就不是有效的叫声。第一个叫声缺了一个a,多了一个o。第二个叫声少了一个k。第二个难点就是在于找到最少的青蛙数目。
首先贡献一个自己的代码。这个代码虽然冗长,但是我觉得还是很好的描述了思路。首先我们考虑第一个问题,我们如何判断string内是否是有效的叫声。首先,我们可以将这个字符串拆分成这样。
例子: “crcoakroak”.
| 字符 | c | r | o | a | k |
|---|---|---|---|---|---|
| 出现坐标 | 0 | 1 | 3 | 4 | 5 |
| 出现坐标 | 3 | 6 | 7 | 8 | 9 |
我们把每一个字符出现的位置按照从小往大进行排列。通过这样的排列方法我们可以判断两个事情,第一个是有没有多余的或者缺少的字符。第二个是每一个字符出现的位置是不是正确的。有一个细节需要说明,我们对除了’k’之外的每一个字符,我们都尽可能的匹配离其位置最近的下一位字符。比如说对于第一个’c’来说,我们肯定匹配位置1的’r’,而不是位置6的’r’。这也是一种greedy的做法。我们可以很直观的看出来,我们就是在横坐标上面循环"croak"这个字符串,检查每一个字符出现的位置是否正确。这一步是在第一个while loop当中完成的。同时,在循环查找我们需要一个frogs链表记录每一声蛙叫开始的时间和结束的时间。这是为下一步做准备。
当我们验证完这个输入的叫声是有效的之后。我们就可以参考 253.Meeting Rooms II的做法了。但是在这里我们不用融合而是利用扫描线的办法,如果有一个蛙叫在另一个蛙叫结束之前就叫了,说明我们需要在这个区间增加一个蛙叫。我们将起始和结束的蛙叫都放入frogs数组当中。起始位置增加1,结束位置减少1。我们还是举上面这个例子。此时我们获得了两个区间[0,5]和[3,9]代表第一声蛙叫和第二声蛙叫出现的时间段。
我们可以画出如下时间线
| 坐标 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|---|
| 数值 | 1 | 1 | -1 | -1 |
我们给所有的数值按照位置排序就形成了上面的时间线,[位置,数值] 有 [0,1] , [3,1] , [5,-1] , [0,-1]。当我们按照顺序循环每个位置的时候同时累加数字,我们发现在在这个过程当中累加和最大为2。所以结果就是我们最多需要两只青蛙。我们可以自行给上面时间线添加新的区间,就比较好理解了。
时间复杂度,因为最后涉及到给所有的区间排序,最多会出现(n/5)个区间,所以时间复杂度是O(NLOGN),
空间复杂度: O(N)
解法一:
class Solution {
public int minNumberOfFrogs(String croakOfFrogs) {
Map<Character, List<Integer>> map = croakPositionMapping(croakOfFrogs);
List<int[]> frogs = new ArrayList<>();
char[] croak = new char[]{'c','r','o','a','k'};
while(!map.isEmpty()){
if(!map.containsKey('c')) return -1;
int firstPos = map.get('c').get(0);
int prevPos = firstPos;
removeElementFromMap(map, 'c');
for(int i=1; i<=4; i++){
char c = croak[i];
if(!map.containsKey(c)) return -1;
int curPos = map.get(c).get(0);
if(curPos < prevPos) return -1;
prevPos = curPos;
removeElementFromMap(map, c);
}
int lastPos = prevPos;
frogs.add(new int[]{firstPos, 1});
frogs.add(new int[]{lastPos, -1});
}
Collections.sort(frogs, (a,b)->a[0]-b[0]);
int total =0, res = 0;
for(int[] p:frogs){
total+=p[1];
res = Math.max(res, total);
}
return res;
}
public Map<Character, List<Integer>> croakPositionMapping(String croakOfFrogs){
Map<Character, List<Integer>> map = new HashMap<>();
for(int i=0; i< croakOfFrogs.length(); i++){
char c = croakOfFrogs.charAt(i);
if(!map.containsKey(c)) map.put(c, new LinkedList());
map.get(c).add(i);
}
return map;
}
public void removeElementFromMap(Map<Character, List<Integer>> map, char c){
map.get(c).remove(0);
if(map.get(c).size() == 0) map.remove(c);
}
}
解法二:
这个解法更加聪明,转载自 链接. 首先可以参考他画的这个图。
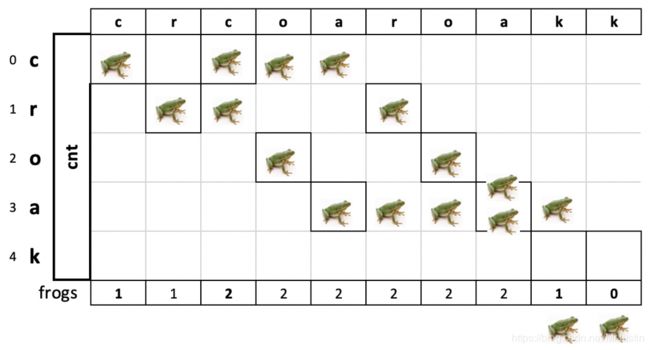
其实核心的思想还是扫描线的思想,但是把判断叫声的这一步大大的简化了,我们每一次遇到除第一位的‘c’和最后一位’k‘以外。直接将当前字符的上一位字符个数减一。如果上一位减一之后小于0了,说明当前一位字符的前一位没有字符与之匹配了。
假设我们这个输入是"crok",当我们遍历到k的时候,他的上一位’a’所在的位置为0,说明我们多了一个字符串k。所以没有办法匹配了。这个办法很聪明。
其余的就是跟扫描线做法一样了,当遇到新的c的时候,我们增加一个frog,遇到k的时候。我们减少一个frog。
public int minNumberOfFrogs(String croakOfFrogs) {
int cnt[] = new int[5];
int frogs = 0, max_frogs = 0;
for (var i = 0; i < croakOfFrogs.length(); ++i) {
var ch = croakOfFrogs.charAt(i);
var n = "croak".indexOf(ch);
++cnt[n];
if (n == 0)
max_frogs = Math.max(max_frogs, ++frogs);
else if (--cnt[n - 1] < 0)
return -1;
else if (n == 4)
--frogs;
}
return frogs == 0 ? max_frogs : -1; //如果最后所有的青蛙都叫完了的话
}
解法三:
这个跟上面的解法差不多,优化了查询位置的时间。直接对比每一步的结果。如果当前字符位的个数比上一位多,那么说明当前位没有办法被匹配成功。
class Solution {
public int minNumberOfFrogs(String croakOfFrogs) {
char[] ch = croakOfFrogs.toCharArray();
int curr = 0;
int res = 0;
int c = 0, r = 0,o = 0,a = 0, k = 0 ;
for(int i = 0; i < ch.length; i++) {
if(ch[i] == 'c') {
c++;
curr++;
} else if(ch[i] == 'r') {
r++;
} else if(ch[i] == 'o') {
o++;
} else if(ch[i] == 'a') {
a++;
} else {
k++;
curr--;
}
res = Math.max(res, curr);
if(c < r || r < o || o < a || a < k) {//要满足所有的条件
return -1;
}
}
if((c == r) && (r == o ) && ( o == a) && (a == k)) {
return res;
}
return -1;
}
}