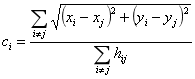无线定位技术的基本原理(模型)及测距技术总结
定位算法根据是否利用测量点的距离关系,分为基于测距的定位算法(range-based)和非基于测距(range-free)的定位算法两类。不同的测距方法主要的差别在于如何获得两个节点之间的距离关系(后者是角度差),也就是说不同的测距方法主要在于他们获得两个节点之间的距离或者角度方式的不同。其中,基于测距的定位模型主要分为以下几种:基于圆周的定位模型、双曲线定位模型、三角定位模型。而基于非测距的定位模型主要 K 最近邻居法、
DV-HOP 法、三角质心法和加权三角形质心法。
基于测距的定位模型
根据测量手段和所建立的数学模型的不同,主要分为基于测量信号接收功率(RSSI)、基于信号到的角度(AOA)、基于信号到达时间(TOA/TDOA)这三种测量方法。对应于不同的定位算法,适当地应用与之匹配的数学模型。
基于圆周的定位模型
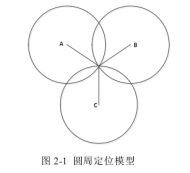
基于圆周的定位模型的原理在于根据未知节点与多个已知节点(n大于或等于3)的距离长度为半径,并以已知节点为圆心获得的多个圆,这些圆相交的点 M 即为未知节点的位置,如图2-1所示:
双曲线模型
基于双曲线定位模型的原理如下:首先假设通过某特定的测量方法得到未知节点到
两个已知节点 A,B 之间的距离差,即2a,根据有关双曲线的数学方程得:
![]() (2-2)
(2-2)
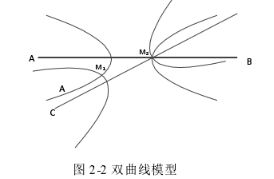
其中,M 是双曲线上一点,F1和F2分别是双曲线的两个焦点,2a 是两焦点之间的距离。那么,根据公式(2-2)可以得出:未知节点 M 就在以两个已知节点 A,B 的位置为焦点,距离差是 2a 的双曲线上。同样的,根据另外一个已知节点 C,同样可以在确定2条双曲线,就这样,两个双曲线的交点即为未知节点 M 的位置。其模型如图 2-2 所示
双曲线模型一共利用了三个已知节点的信息,而通过三个已知节点可以得到的两个双曲线,最后可以确定两个交点。此时,我们可以根据其他一些条件,例如入射角度等信息再进行二次判别,从而排除干扰点的坐标而最终获得未知节点的坐标。
三角定位模型
三角定位模型的原理:首先根据两个已知节点 A,B 之间的距离和他们的位置,以及未知节点 M 与 A,B 的两条连线与直线 AB 所形成的角度α与β,可以求得 M 的位置,即以两个已知节点 A,B 为端点的两条射线的交点上,如图2-3所示
![]()
以三角定位模型为基础的定位算法有AOA(Angle Of Arrival)等,即通过测量信号的到达角而得到节点 M 的位置信息。AOA
的优点是它是利用已知节点数量最少的一种定位算法,如图所示,它只要利用两个已知节点信息就可以计算出未知节点的位置。
基于非测距的定位模型
由于在现实环境中,对测量信号的干扰种类很多而且强度很难预估计,所以基于测距的定位模型对设备的要求比较高。而且这正因为如此,基于这类模型的算法对所测得距离或者角度的要求精度相对高很多,也使得用基于测距的定位模型测得未知节点的位置信息的方法是,要利用较好的设备,从而大大的提高了定位成本。
现实情况来讲,基于非测距的定位模型的精确度绝大部分要低于基于测距的定位模型。
比较典型的定位算法有:K最近邻居法、DV-HOP、DV-distance、凸规划算法、K-N法、包含未知节点的区域取交集的算法和基于多跳的定位算法。
K最近邻居法:
根据信号传播随着距离的增加,信号强度衰减的原理,理论上可以认为,
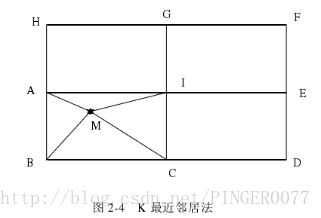
离锚节点越近的未知节点,其接收到的 RSSI 值就会越大。同样的,可以说,当接收的RSSI 越大时,未知节点在该锚节点的附近的概率就会越高,并且在该锚节点附近区域半径就会越小。所以,当在预先布置好锚节点位置的网格中,选取其中离未知节点相对近的 n个锚节点,则锚节点应该位于由n个锚节点组成的多边形内,如图2-4所示。
当确定了距离未知节点M较近的n' 个锚节点后,取由n' 个锚节点为顶点的多边形质心,即所估算的 M点的位置。这种模型的优点是多边形取质心的原理简单,操作起来容易。而其确定是,最后确定的定位精度相当大的程度上取决于预先布置好的锚节点网格密度。当他们的网格密度较小的时候,精确度会相对高一些,当他们的网格密度较大时,精确度也会随之降低。
DV-Hop法
相比于 K最近邻居法,DV-Hop 法与其的区别是:DV-Hop 法可以不需要测量两个节点间的信号强度(K最近邻居法虽不用测得 RSSI 的具体指,却要确定n个锚节点之间的RSSI 值的对比等级)。所以,对于没有硬件条件来满足测 RSSI 的实验人员来说,DV-Hop法可以满足他们的要求.DV-Hop 法的基本思想:通过未知节点与锚节点之间的平均每跳距离与跳数来确定连个节点之间的距离。
其中ci表示未知节点(xi,yi)与锚节点(xj,yj)(j=1,2,…,n)之间的平均每跳距离,hij表示未知节点(xi,yi) 与锚节点(xj,yj)(j=1,2,…,n)之间的跳数,ci则表示他们之间的距此方法在开始运算之前,需要多次通过锚节点向附近广播得到采样数据库,从而在求得平均值之后得到相应的两个已知节点之间跳数,最后将这样的跳数信息应用于整个区域网络。在开始运算之后,选取与未知节点之间跳数相对少的锚节点,将此锚节点的ci作为未知节点的平均每跳距离计算。这样就可以计算出该未知节点到各个锚节点之间的距离,然后通过建立锚节点的三角形网络求得未知节点的位置信息。
质心法与加权质心法
质心法是一种不利用无线信号测量技术的定位算法,他仅需要所有锚节点之间的连通性,利用他们之间的连通通信来去顶未知节点的位置信息。该方法相对简单,而且也容易实现。
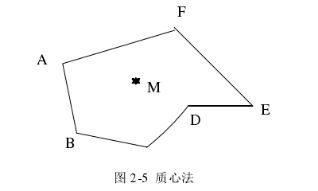
质心法的定位思想:首先,未知节点所处的环境中的所有锚节点向其周围广播一个有特定周期的无线信号,该信号包含这个锚节点自身的 ID 信息和它本身所处的位置信息。当未知节点经过一系列的初始化过程后,它可以收到来自其周围的各个锚节点的信号,当所接收到的不同锚节点信号数量达到一定阈值时,可以认为被接收到信号的锚节点处于连通状态。而由这些锚节点为顶点,可以组建成一个多边形,而这个多边形的质心就作为未知节点的位置。其图示如 2-5(M 为未知节点)所示
设在锚节点广播其 ID 与位置信息,后,未知节点接收到的不同锚节点的信息数量为k,则根据多边形质心公式得其估计坐标为(x0,y0),其公式如下:
其中![]() 为未知节点接收到的不同已知节点的坐标。
为未知节点接收到的不同已知节点的坐标。
综上,质心法不需要未知节点与锚节点之间的相互协调,它主要是由不同锚节点之间的连通性决定的。然而,不难看出,质心法的精确度很大程度上取决于区域内锚节点的分布关系。当锚节点分布越密集并且均匀,它的精确度越高;而当锚节点分布密度低时,一方面不利于构建多边形,一方面也对定位精确度有很大程度上的影响。
基于 RSSI 的加权质心法,很大程度上提高了质心法精确度。它在质心法的基础上引入了锚节点对于未知节点的影响力的思想。由于所接收到的 RSSI值越高,判定其影响力越大,从而相应加大计算中的权值。然而,这种算法不仅在硬件方面需要提高,而且由于要计算所接收到 RSSI 而使得计算量增加,从而提高定位成本。并且这样的定位算法就不单单需要锚节点之间的连通性,还要一定的距离关系,这就使得它处于基于测距与非基于测距两类模型之间。
典型的无线测距技术
通过无线电信号来测得节点之间的距离是该技术的主要目的,而在达到目的的同时,怎样提高精确度也是很重要的研究课题。目前,在该技术领域,主要有一下几个技术:RSSI、TOA、TDOA 和 AOA 技术。
RSSI技术
RSSI,即接收信号强度指示,英文为 Received signal strength Indicator。RSSI 技术主要是根据节点接收到的信号强度值,通过传播信号的经验或理论模型公式,直接转换成其距离值。而距离的转化精度很大程度上取决于所利用的模型公式的准确性。通常情况下,RSSI 技术的精确度并不高。理论上,由于随着距离的增加,由于无线信号的衰减,所接受到的 RSSI 会降低。所以根据这样的关系,可以直接通过RSSI值求得两个节点直接的距离量。而在实际情况下,研究人员通常利用 RSSI 与距离之间的换算模型,将监测到的信号强度值转化成距离值。
在自由空间中,RSSI 值与d2(接收信号设备与发射信号设备之间的距离)成比例减少。在实际环境中,影响 RSSI 值的主要因素是多径效应,多径效应使得到达信号接收设备的频率值是由多种不同振幅、不同相位的干扰波与原来所发射的信号进行的重构的信号频率,从而造成了频率选择性衰落,即所测 RSSI 值的误差。其次影响接收的 RSSI 的是阴影效应,即当消除环境中的频率选择性衰落后,RSSI 值因信号传播过程中,遇到障碍物而产生误差。另一种影响 RSSI 产生误差的原因在于传播新号在路径上的损失。所测量的 RSSI 值是接收信号设备与发射信号电池型号的不同,使得接受到的频率也有差异。
TOA技术
到达时间(TOA)技术主要是应用电磁波的传播来测量信号发射端与接收端之间的距离。这个方法主要指:由于信号发射端发射的信号传播的速度为光速,设为 c,而信号从发射端到接收端所传播的时间为 t,则信号从发射端到接收端之间的距离为 t*c。由于光的传播速度十分快,所以这种技术很容易产生误差。目前 TOA 技术主要应用于有 GPS和 UWB
的定位系统中。 根据 TOA 中发射信号和接收信号的对象是否相同,将它的模式分为两类,即 A 类和B 类。A 类模式指的是信号发送端与接收端有着同样的时钟同步系统,信号在离开发射端与到达接收端时分别记录时间节点,这样最后做差,即可求得传播时间。这种模式在 GMS系统中极为常见,并且由于设备精良可以说误差很小。B 类模式指的是当信号从发射信号端出发到再次返回发射端都记录一下它的时间节点(当信号到达信号接收端是可能会有一定量可知的时间延迟,可以最后减去),这样经过做差在取其中值,既可以得到信号传播的时间。在这类模式下,信号发射端的计时器的始终脉冲宽度主要决定了它的定位准确度。
TDOA技术
TDOA(时间到达差,Time Difference of Arrival)技术在无线测距方面得到广泛应用。TDOA 通过两个不同的无线信号到达信号接收端的时间差及已知的两个不同无线信号的传播速率,计算信号发射端到信号接收端之间的距离 d。
节点 A 发射两种传播速率不同的无线信号(中间可能有延迟),当节点 B 接收到第一种信号时开始计时(接收信号后可能延迟一段时间后开始计时),当收到第二种信号时结束计时。则节点 A 与节点 B 之间的距离 d 可表达为如公式 2-5(无延迟情况)。
其中V1为传播速率较快的无线信号传播速率,V2为传播较慢的信号传播速率,t 为不同信号到达信号接收端的时间差。
在视距条件下,通过 TDOA 技术的求得的距离值的测量精度还是相当可观的,但是该方法对硬件设施要求比较高,而且测试过程要克服回声干扰和空气湿度、温度对信号传播速度的影响。
AOA技术
AOA(到达角度, Angle of Arrival)技术,主要是根据信号接收端接收到的各个发射信号端发射信号的到达角度不同,定位出信号接收端的绝对位置坐标。
该技术受外界影响严重,而且对环境要求较高。噪声或多径效应等都会对测量结果产生比较大的影响。同时该技术在信号接收端要额外附加无线电信号感知器件,在成本、硬件体积、功耗等代价较大,且对视距要求也比较高,从而极大程度地限制了该技术在无线测距技术上的应用。