cs221n学习笔记——词表示
词向量
localist representation
把词作为离散符号表示
如ont-hot编码
缺点:
1. 两个词向量之间是正交的
2. ont-hot编码向量之间没有相似性
distributed representaion(word embedding)
示例
学习算法决定了word vector是什么
下图是embedding后词表示的一个例子(来自cs221n)
模型
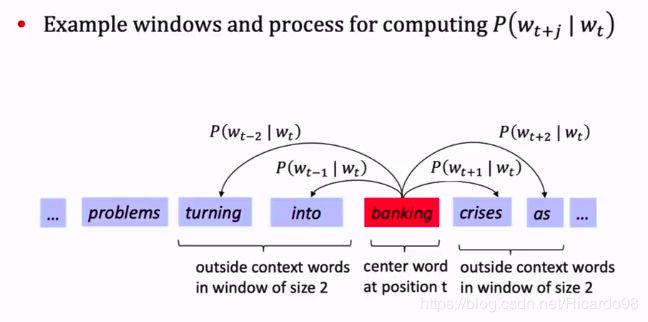
似然率=
L ( θ ) = ∏ t = 1 T ∏ − m ≤ j ≤ m P ( w t + j ∣ w t ; θ ) L(\theta)=\prod_{t=1}^{T} \prod_{-m \leq j \leq m} P\left(w_{t+j} | w_{t} ; \theta\right) L(θ)=t=1∏T−m≤j≤m∏P(wt+j∣wt;θ)
θ \theta θ代表所有的词向量
最大化log概率(也用可以最小化)
1 T ∑ t = 1 T ∑ − c ≤ j ≤ c , j ≠ 0 log p ( w t + j ∣ w t ) \frac{1}{T} \sum_{t=1}^{T} \sum_{-c \leq j \leq c, j \neq 0} \log p\left(w_{t+j} | w_{t}\right) T1t=1∑T−c≤j≤c,j=0∑logp(wt+j∣wt)
取Log是因为对数似然方程更容易计算
where c is the size of the training context (which can be a function of the center word w t w_t wt ). Larger c results in more training examples and thus can lead to a higher accuracy, at the expense of the training time.
p ( w O ∣ w I ) = exp ( v w O ′ ⊤ v w I ) ∑ w = 1 W exp ( v w ′ ⊤ v w I ) p\left(w_{O} | w_{I}\right)=\frac{\exp \left(v_{w_{O}}^{'\top} v_{w_{I}}\right)}{\sum_{w=1}^{W} \exp \left(v_{w}^{'\top} v_{w_{I}}\right)} p(wO∣wI)=∑w=1Wexp(vw′⊤vwI)exp(vwO′⊤vwI)
v w O ′ T v w I = v w O ′ T . v w I = ∑ i = 1 n v w O v w I v^{'T}_{w_O} v_{w_I}=v^{'T}_{w_O}. v_{w_I}=\sum_{i=1}^{n} v_{w_O} v_{w_I} vwO′TvwI=vwO′T.vwI=∑i=1nvwOvwI点积极计算相似度,点积越大,概率越大
分母的作用是通过标准化整个词汇表来获得概率分布
where v w v_{w} vw and v w ′ v'_{w} vw′ are the “input” and “output” vector representations of w w w, and W W W is the number of words in the vocabulary. This formulation is impractical because the cost of computing ∇ l o g p ( w O ∣ w I ) ∇ log p(w O |w I ) ∇logp(wO∣wI) is proportional to W , which is often large ( 1 0 5 10^5 105 – 1 0 7 10^7 107 terms).
训练
Hierarchical Softmax
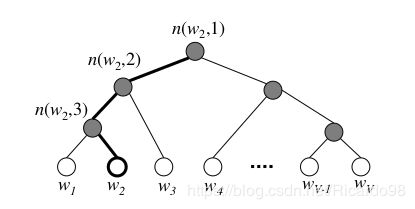
层次softmax使用二叉树表示W的输出层,从根节点到某个词w的节点的路径。白点是词汇表里的词,黑点是inner units,highlight的path代表 L ( w 2 ) = 4 L(w_2)=4 L(w2)=4
p ( w ∣ w I ) = ∏ j = 1 L ( w ) − 1 σ ( [ n ( w , j + 1 ) = ch ( n ( w , j ) ) ] ⋅ v n ( w , j ) ′ ⊤ v w I ) p\left(w | w_{I}\right)=\prod_{j=1}^{L(w)-1} \sigma\left([n(w, j+1)=\operatorname{ch}(n(w, j))] \cdot v_{n(w, j)}^{'}{\top} v_{w_{I}}\right) p(w∣wI)=j=1∏L(w)−1σ([n(w,j+1)=ch(n(w,j))]⋅vn(w,j)′⊤vwI)
-
σ ( x ) = 1 1 + e x p ( − x ) \sigma(x)=\frac{1}{1+exp(-x)} σ(x)=1+exp(−x)1
-
[x]=1 if x is true ;[x]=-1 otherwise
优势:
1.The main advantage is that instead of evaluating W output nodes in the neural network to obtain the probability distribution, it is needed to evaluate only about l o g 2 ( W ) log_2 (W ) log2(W) nodes
2.the cost of computing l o g p ( w O ∣ w I ) log_p(w_O |w_I ) logp(wO∣wI) and ∇ l o g p ( w O ∣ w I ) ∇ log_p(w_O |w_I ) ∇logp(wO∣wI) is proportional to L ( w O ) L(w_O ) L(wO), which on average is no greater than l o g ( W ) log(W) log(W)
Negative Sampling
本质是预测总体类别的一个子集
log σ ( v w O ′ ⊤ v w I ) + ∑ i = 1 k E w i ∼ P n ( w ) [ log σ ( − v w i ′ ⊤ v w I ) ] \log \sigma\left(v_{w_{O}}^{\prime \top} v_{w_{I}}\right)+\sum_{i=1}^{k} \mathbb{E}_{w_{i} \sim P_{n}(w)}\left[\log \sigma\left(-v_{w_{i}}^{\prime \top} v_{w_{I}}\right)\right] logσ(vwO′⊤vwI)+i=1∑kEwi∼Pn(w)[logσ(−vwi′⊤vwI)]
代码
gensim库
import gensim
model=gensim.models.Word2Vec(sentences, sg=1, size=100, window=5, min_count=5, negative=3, sample=0.001, hs=1, workers=4)
sentences=gensim.models.Word2Vec.Text8Corpus(file)
model.save(fname)
model = gensim.models.Word2Vec.load(fname)
此处训练集的格式为英文文本或分好词的中文文本
1.sg=1是skip-gram算法,对低频词敏感;默认sg=0为CBOW算法。
2.size是输出词向量的维数,值太小会导致词映射因为冲突而影响结果,值太大则会耗内存并使算法计算变慢,一般值取为100到200之间。
3.window是句子中当前词与目标词之间的最大距离,3表示在目标词前看3-b个词,后面看b个词(b在0-3之间随机)。
4.min_count是对词进行过滤,频率小于min-count的单词则会被忽视,默认值为5。
5.negative和sample可根据训练结果进行微调,sample表示更高频率的词被随机下采样到所设置的阈值,默认值为1e-3。
6.hs=1表示层级softmax将会被使用,默认hs=0且negative不为0,则负采样将会被选择使用。
7.workers控制训练的并行,此参数只有在安装了Cpython后才有效,否则只能使用单核。
References
[1] 秒懂词向量Word2vec的本质
[2] Mikolov, T., Sutskever, I., Chen, K., Corrado, G. S., and Dean, J. (2013b). Distributed
representations of words and phrases and their compositionality. In Advances in Neural
Information Processing Systems,