LogisticRegression R 手写实现

1.读取数据

[数据来源:https://en.wikipedia.org/wiki/Logistic_regression]

rm(list=ls())
setwd("C:\\Users\\xiaokang\\Desktop\\课程\\博一下学期\\广义线性模型\\")
data=read.csv("Simulation\\dataset\\LogisticRegression\\exam_pass.csv")
print(data)
#这里我发现了Rmarkdown的一个警告，因为我在这里修改了默认的工作路径，
#但是 Rmarkdown提醒了我：我的工作路径已经改变了

可以看到该数据集只有20个样本；其中Hours表示学生考试复习用的时间；Pass=1表示学生通过考试；Pass=0表示学生并没有通过考试。

2.可视化

library(ggplot2)
ggplot(data=data,aes(x=Hours,y=Pass))+geom_point()

可以看到，只有一个变量$Hours$,那么如果判别函数是线性函数，即分类平面等价于$Hours=c$,当$Hours<c$时，判定为考试不合格，当$Hours>c$时，判定为不合格，从图像上看，此数据显然是线性不可分的数据集，例如存在一个$Hours=1.75$,但该学生考试及格了，但是又有比他用的时间多的点考试不合格。所以建立的LogisticRegression的准确率肯定不能达到100%

3.使用R自带的glm函数拟合logisticRegression

library(stats)
data=as.data.frame(data)
y.glm=glm(Pass~Hours,family=binomial(link="logit"),data=data)
print(summary(y.glm))
print(y.glm$fitted.values)
print(predict(y.glm))
pred_val=y.glm$fitted.values>0.5
sprintf("一共预测正确了%d个样本",sum(pred_val==data$Pass))
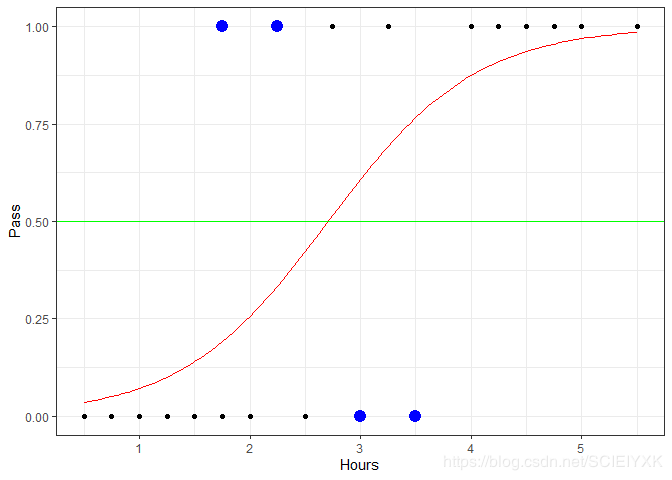
print("预测错误的Hours为：");print(data$Hours[pred_val!=data$Pass])
# 分别是第 7, 9，12，14

可以看到和维基百科上拟合的效果完全一致,其中得到的判定函数为$p(Y=1|Hours)=\frac{e^{-4.0777+1.5046Hours}}{1+e^{-4.0777+1.5046Hours}}=\frac{1}{1+e^{4.0777-1.5046Hours}}$,可以看到地方$predict(y.glm)$预测的是$-4.0777+1.5046\times Hours$的值
而$y.glm$fitted.values$表示的是$Y=1$的概率

4.手写实现logisticRegression

(1)损失函数：交叉熵 (2)优化算法：梯度下降

4.1 计算损失函数

交叉熵公式 $H(p)=-[p\ast log(p)+(1-p)\ast log(1-p)]$

cross_entropy=function(y_pre,y_true)
{
  return(-sum(y_true*log(y_pre)+(1-y_true)*log(1-y_pre)))
}

首先需要注意的是交叉熵是有一个负号的，我开始少了一个负号，结果已知在预测的值一直是0.5。

4.2 计算梯度

$\frac{\partial loss}{w_0}$与$\frac{\partial loss}{w_1}$

其中$loss={\sum }_1^n-[y_{i}log(p)+(1-y_i)\ast log(1-p)$,其中$Pr(Y=1|x)=\frac{e^{w_0+w_{1}x}}{1+e^{w_0+w_{1}x}}$,这里$loss$函数可以进一步化简的，不是很麻烦

SGD=function(w0,w1,x,y)
{
  #本来觉得R应该也可以进行符号运算，试了一下，R的符号运算很烂，做不了
  sgd={};
  diff_w0=-(sum(y)-sum(exp(w0+w1*x)/(1+exp(w0+w1*x))))#直接手算
  diff_w1=-(sum(x*y)-sum(x*exp(w0+w1*x)/(1+exp(w0+w1*x))));#直接手算
  sgd$w0=-diff_w0;
  sgd$w1=-diff_w1;
  return(sgd)
}

4.3 计算预测的概率，并不是0，1

pred_logistic=function(w0,w1,x)
{#直接让x是向量算了
    prob_1=exp(w0+w1*x)/(1+exp(w0+w1*x))
    return(prob_1)
}

4.4 计算正确率

cal_accuracy=function(w0,w1,x,y)
{
  #browser()
  num=(exp(w0+w1*x)/(1+exp(w0+w1*x))>0.5)
  #sprintf("有%d个预测正确了",sum(num==y))
  accuracy=sum(num==y)/length(x)
  return(accuracy)
}

4.5 迭代过程

设置$w_0=0,w_1=0$为初始值，学习速率为0.01

iter_max=10000 #当1000次时并没有自己收敛到维基百科上的值
learn_rate=0.01;
w0=0.0;
w1=0.0;
cro_enr=NULL
plot_w0=w0;
plot_w1=w1;
for(i in c(1:iter_max))
{
   
    y_pred=pred_logistic(w0,w1,data$Hours);
    cro_enr=c(cro_enr,cross_entropy(y_pred,data$Pass));
    acc=cal_accuracy(w0,w1,data$Hours,data$Pass)
    update=SGD(w0,w1,data$Hours,data$Pass)
    w0=w0+learn_rate*update$w0;
    w1=w1+learn_rate*update$w1;
    plot_w0=c(plot_w0,w0)
    plot_w1=c(plot_w1,w1)
}
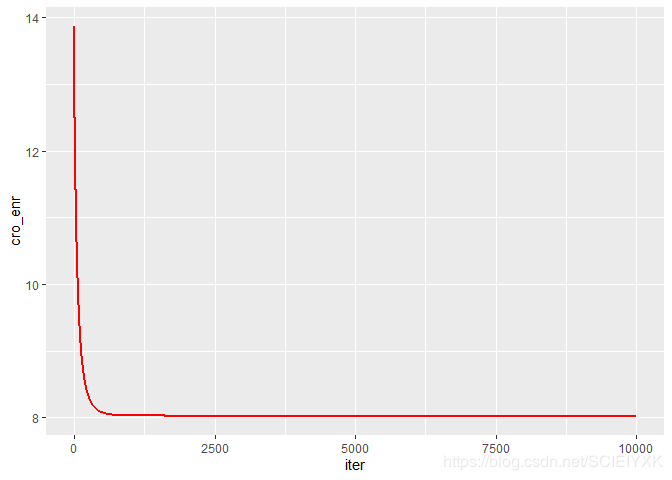
sprintf("最终算法预测结果的交叉熵为：%.4f",cross_entropy(y_pred,data$Pass))
sprintf("最终预测的准确率是%.3f",acc)
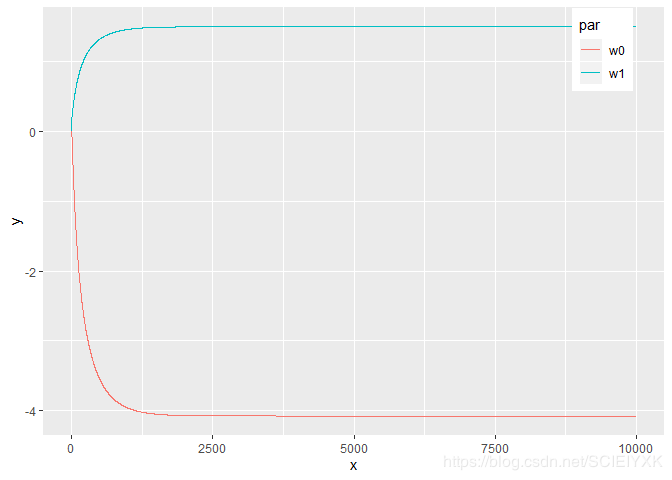
sprintf("根据SGD算法，迭代10000次后,w0,w1的值为%.4f,%.4f",w0,w1)

5 最终分析

5.1 画出$Pr(Y=1|x)$的函数图

h=c(7,9,12,14);
logistic_curve=function(x) 1/(1+exp(4.0777-1.5046*x))
ggplot(data=data,aes(x=Hours,y=Pass))+geom_point()+theme_bw()+stat_function(fun=logistic_curve,color="red")+geom_hline(yintercept=0.5,color="green")+geom_point(data=data[h,],aes(x=Hours,y=Pass),color="blue",size=4)

5.2 $loss$函数图

iter=c(1:10000)
data2=data.frame(x=iter,y=cro_enr);
ggplot(data=data2,aes(x=iter,y=cro_enr))+geom_line(color="red",size=1)

5.2 $w_0,w_1$迭代数值变化图

iter=c(0:10000)
cor1=rep("w0",10001)
cor2=rep("w1",10001)
data3=data.frame(x=c(iter,iter),y=c(plot_w0,plot_w1),par=c(cor1,cor2))
ggplot(data=data3,aes(x=x,y=y,colour=par))+geom_line()+theme(legend.position=c(0.9, 0.9))