【PyTorch学习笔记】22:使用nn.RNN构建循环网络预测序列数据的例子
简述
在这个例子中,从 [ k , k + n ) [k,k+n) [k,k+n)时刻的正弦函数,要去预测 [ k + t , k + n + t ) [k+t,k+n+t) [k+t,k+n+t)时刻的正弦曲线。

因为在每个时刻曲线上的点是一个值,所以这个例子中不需要做embedding,也就是feature_len=1。如果要给出49个时刻的点,也就是seq_len=49。如果只提供一条曲线在训练时喂入,也就是batch=1。按照之前学的表示法,输入的shape是:
[ s e q _ l e n , b a t c h , f e a t u r e _ l e n ] = [ 49 , 1 , 1 ] [seq\_len,batch,feature\_len]=[49,1,1] [seq_len,batch,feature_len]=[49,1,1]
这节的例子中使用batch提前的表达方式,即输入的shape是:
[ b a t c h , s e q _ l e n , f e a t u r e _ l e n ] = [ 1 , 49 , 1 ] [batch,seq\_len,feature\_len]=[1,49,1] [batch,seq_len,feature_len]=[1,49,1]
注意,在程序中nn.RNN后面加了一个线性层,因为它直接输出来的是按照隐藏记忆单元的尺寸,这里就是把输出的 [ s e q _ l e n , b a t c h , h i d d e n _ l e n ] [seq\_len,batch,hidden\_len] [seq_len,batch,hidden_len]变换成 [ s e q _ l e n , b a t c h , f e a t u r e _ l e n ] [seq\_len,batch,feature\_len] [seq_len,batch,feature_len]。
程序
特别注意,因为设置了batch_first=True,所以这里nn.RNN模块的输入输出包括隐藏记忆单元全部都是把batch这个维度放到最前面了。
import torch
import numpy as np
from torch import nn, optim
from matplotlib import pyplot as plt
"""
解决这个问题构建的完整的循环网络
"""
hidden_len = 16 # 隐藏记忆单元尺寸
class Net(nn.Module):
def __init__(self):
super(Net, self).__init__()
# RNN层
self.rnn = nn.RNN(
input_size=1, # 即feature_len=1
hidden_size=hidden_len, # 隐藏记忆单元尺寸
num_layers=1, # 层数,这里就用单层RNN
batch_first=True # 在喂入数据时,按照[batch,seq_len,feature_len]的格式
)
# 对RNN层的参数做初始化
for p in self.rnn.parameters():
nn.init.normal_(p, mean=0.0, std=0.001)
# 输出层,直接用一个线性变换把每个时刻记忆单元的hidden_len输出为所需的feature_len=1
self.linear = nn.Linear(hidden_len, 1)
def forward(self, x, h):
"""
注意这里的输入输出全部都变成batch提前的!
:param x:一次性输入所有样本所有时刻的值(batch,seq_len,feature_len)
:param h:第一个时刻空间上所有层的记忆单元(batch,num_layer,hidden_len)
:return:输出out(batch,seq_len,hidden_len)和h(batch,num_layer,hidden_len)
"""
out, h = self.rnn(x, h)
# 因为要把输出传给线性层处理,这里将其batch和seq_len维度打平在一起
# 这样就能只变换最后一个维度hidden_len
out = out.view(-1, hidden_len) # shape从(1,seq_len,hidden_len)变成(seq_len,hidden_len)
out = self.linear(out) # shape从(seq_len,hidden_len)变成(seq_len,feature_len=1)
# 再把batch=1这个维度添加回最前面,使维度不变(因为要和训练集给定的y做MSE)
out = out.unsqueeze(dim=0) # shape从(seq_len,feature_len=1)变成(1,seq_len,feature_len=1)
return out, h
# -----------------------------------------------------------
"""
训练过程
"""
lr = 0.01 # 学习率
model = Net() # 得到网络实例模型
criterion = nn.MSELoss() # 用于计算MSE损失
optimizer = optim.Adam(model.parameters(), lr) # 用Adam优化器,传入要优化的参数和学习率
# 初始化记忆单元,shape是(batch,num_layer,hidden_len)
h = torch.zeros(1, 1, hidden_len)
"""生成样本数据所使用的一些超参"""
num_points = 50 # 在区间中取多少个样本点
seq_len = num_points - 1 # 实际使用的序列长度
# 循环6000次,每次batch=1
for iter in range(6000):
"""生成样本数据"""
# 在0~3之间随机取开始的时刻点
k = np.random.randint(3, size=1)[0]
# 取点的区间是[k, k+10],均匀地取num_points个点
time_steps = np.linspace(k, k + 10, num_points)
# 在这num_points个时刻上生成函数值数据
data = np.sin(time_steps)
# 将数据从shape=(num_points,)转换为shape=(num_points,1)
data = data.reshape(num_points, 1) # feature_len=1
# 输入前49个点(seq_len=49),即下标0~48
x = torch.tensor(data[:-1]).float().view(1, seq_len, 1) # batch,seq_len,feature_len
# 预测后49个点,即下标1~49
y = torch.tensor(data[1:]).float().view(1, seq_len, 1) # batch,seq_len,feature_len
# 至此,生成了x->y的样本对, x和y都是shape如上面所写的序列
# 喂入模型得到输出
out, h = model(x, h) # h是上次循环得到的h
# 因为h在循环中被一次次嵌套,这里不要为上一个网络求梯度,而只求当前的,所以detach一下
h = h.detach()
# 计算和预期输出之间的MSE损失
loss = criterion(out, y)
# 更新网络参数
model.zero_grad()
loss.backward()
optimizer.step()
# 循环一定次数输出loss
if iter % 1000 == 0:
print("迭代次数:{}, loss:{}".format(iter + 1, loss.item()))
# -----------------------------------------------------------
"""
测试过程
"""
# 先用同样的方式生成一组数据x,y
k = np.random.randint(3, size=1)[0]
time_steps = np.linspace(k, k + 10, num_points)
data = np.sin(time_steps)
data = data.reshape(num_points, 1) # feature_len=1
x = torch.tensor(data[:-1]).float().view(1, seq_len, 1) # batch,seq_len,feature_len
y = torch.tensor(data[1:]).float().view(1, seq_len, 1) # batch,seq_len,feature_len
# 用于记录预测出的点
predictions = []
# 取训练时输入的第一个点,即在x(1,seq_len,1)取seq_len里面第0号的数据
# 这里将输入seq_len'设置为1(而不是49)
# 输入什么长度的数据会自动调整网络结构来给出输出
input = x[:, 0, :]
# 输入的shape变成标准的(batch=1,seq_len'=1,feature_len=1)
input = input.view(1, 1, 1)
# 迭代seq_len次,每次预测出一个点
for _ in range(x.shape[1]):
# 送入模型得到预测的序列,输入了一个点的序列也就输出了(下)一个点的序列
pred, h = model(input, h)
# 这里将预测出的(下一个点的)序列pred当成输入,来给到下一次循环
input = pred
# 把里面那个点的数取出来记录到列表里
# 这里用ravel()而不用flatten(),因为后者是原地操作,会改变pred也就是input
predictions.append(pred.detach().data.numpy().ravel()[0])
# 绘制预测结果predictions和真实结果y的比较
plt.scatter(time_steps[1:], y.data.numpy().ravel())
plt.scatter(time_steps[1:], predictions, c='r')
plt.show()
运行结果:
迭代次数:1, loss:0.47990307211875916
迭代次数:1001, loss:0.001508450135588646
迭代次数:2001, loss:0.0012417093385010958
迭代次数:3001, loss:0.00087927799904719
迭代次数:4001, loss:5.3126928833080456e-05
迭代次数:5001, loss:0.0002698581956792623
需要注意的地方
首先要注意,使用nn.RNN时,输入Tensor的seq_len并不是一个在构造时需要的参数,也就是说,训练的时候可以用某个seq_len训练,而测试的时候可以用另一个seq_len来测试。比如在这个例子中,训练时是用0-48这49个点,预测1-49这49个点(seq_len=49)。而测试时每次传入一个点(seq_len=1),预测下一个点。PyTorch会自动调整循环网络的结构来适应输入。
另外,程序中22至24行对nn.RNN的参数初始化非常重要,如果不进行初始化,其他条件都不变,最终得到的模型预测结果是这样的:
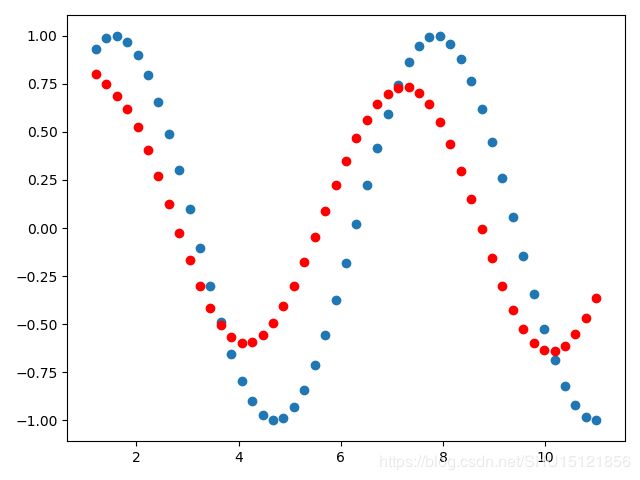
关于优化器更新网络参数前为什么要在每个batch使用model.zero_grad()可以参考这篇。
关于优化器更新网络参数前为什么要使用loss.backward()可以参考这篇。
梯度裁剪
如果发生梯度爆炸,可以进行梯度裁剪:
model.zero_grad()
loss.backward()
for p in model.parameters():
# print(p.grad.norm()) # 查看参数p的梯度
torch.nn.utils.clip_grad_norm_(p, 10) # 将梯度裁剪到小于10
optimizer.step()
