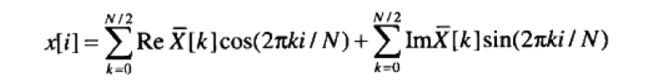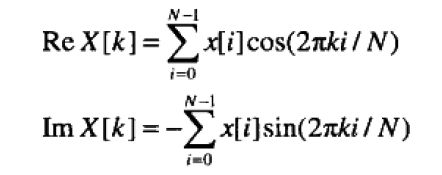傅里叶入门--只要肯努力,弯的都能掰直
记得以前有门课程,有这么一个说法:任何周期函数,都可以看作是不同振幅,不同相位正弦波的叠加。
咳咳。。。
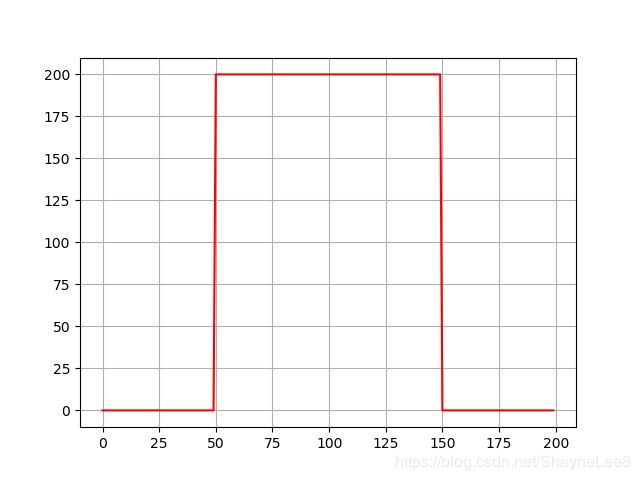
举个栗子,某函数有如下图示形状:
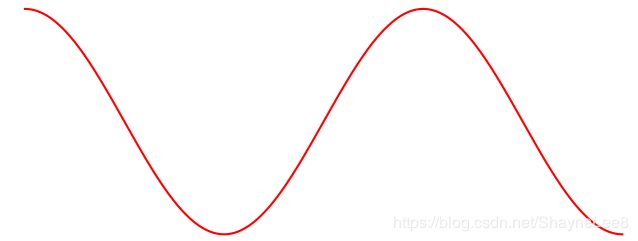
可以由多个形状如下的波形叠加合成。
咋一看,一想,不合理呀,一种弯曲丰满的的曲线怎么会合成横平竖直的直线呢?多个曲线相加莫非就是变高、变宽、变陡或变缓,也不至于平了吧。小学老师告诉我一只羊加一只羊等于两只羊,我信了,但是现在告诉我两只美羊羊加3只懒羊羊等于熊大,我不信!
这是我开始的想法,估计大家也是有和我一样的想法。
当今美颜相机、声音控制、变音、图像识别等对大家都不陌生了,这些图片处理、声音处理等技术,或多或少用到了一种叫做傅里叶变换的东东。想想这是以前课堂里东西呀,情不自禁回忆以前的学校生涯,课堂经常玩手机,懒,学的差,混得low。黑板前那不厌其烦的讲课,说的虽然是汉语但听得比巴基斯坦语还艰难的老师,现在深刻体会到他写的每一行字,说的每一句话都是对的。
出来混,早晚都要还的。想把以前忽略过的东西温习一遍,就当是一次回忆了,顺便练练手,说不定哪天又用到了。
额嗬。。。咳咳。。。以上是无关紧要的叙事。
回到刚开始的问题,在书本上有这么一个公式:
<本文涉及的公式截图来自书籍《实用数字信号处理:从原理到应用》作者:StevenW.Smith>
(大家不要太纠结公式的符号是什么意思,我摆在这只是为了直观的说明问题,不影响本文的讨论内容)
什么意思尼?
用开局第一个图的矩形波为例,这个时域波形有 N=200个信号点。
结合上面公式得出通俗的表达:
200个点组成的矩形波=101个点组成的cos曲线的叠加+101个点组成的sin曲线叠加。
接下我们就开始以轻松愉快的方式来验证这个问题。
怎么个轻松法,比如当成这是一个是真的吗的题目,节目开始:
我们开始来讨论这个是真的吗的问题。
要求得这些曲线还需要一个公式:
这个公式简单理解就是求得每个曲线的振幅。
不同的曲线有不同的振幅,这些曲线就像是声音,不同振幅和不同的频率的声音构成动听的乐章,只是本文的乐章是一个矩形。
做饭的锅,灶已经准备好, 开始炒菜了。
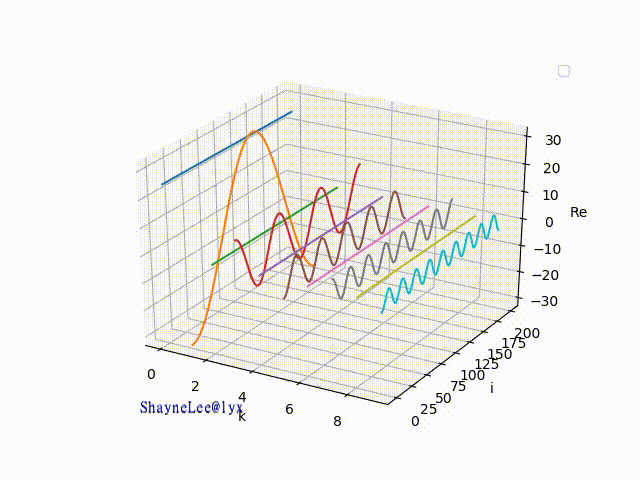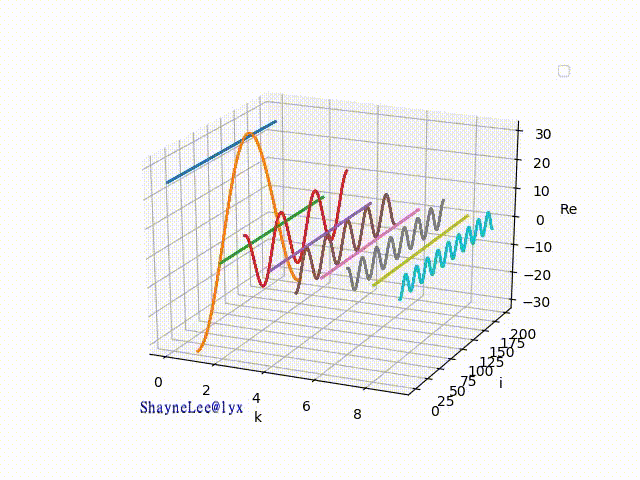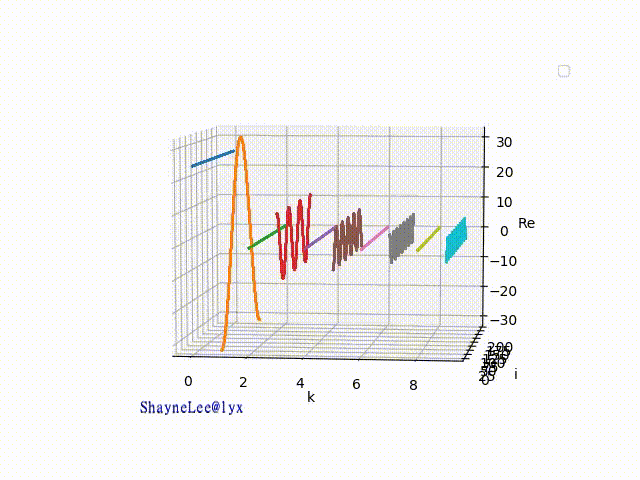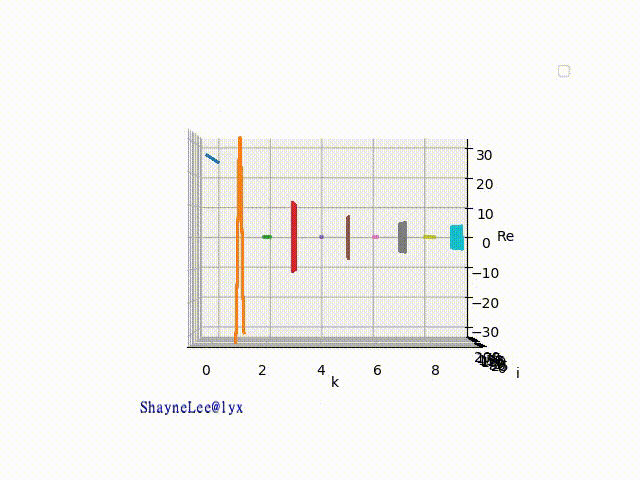
先来把 cos 曲线下锅。(cos 部分在书本里被称为实部)
<下面合成动态图中:绿色代表cos曲线, 蓝色代表上次合成后的线, 红色代表本次叠加结果的线>
开始先用慢火,看先前10 条线合成的过程:
(⊙o⊙)… 是慢慢有点有矩形的样子,但是还是不够像,这菜还不够熟,接下来就火力全开,让子弹飞一会儿。
准备!
action!
101 个曲线能合成:
是不是有点惊讶!肉眼很难看出和矩形的差别了。现在仅是101 条线,你想想如果是无穷个相加那不就是90度的直角了吗。
只要肯努力,弯的都能掰直。真的不是我乱说的,而是有依据的。
细心的人可能会发现有很多y=0的直线,这不是我滥竽充数随便加的,而是公式求出来的振幅就是0。 还有开篇第一图中间部分信号值是200, 怎么曲线叠加之后是50了,这我也真不知道了,我按照书本做就是这样的结果,如果你知道那就告诉我呗。
书本上告诉我们这些曲线构成了该信号的频域。 什么?你问我画出来是什么样子。
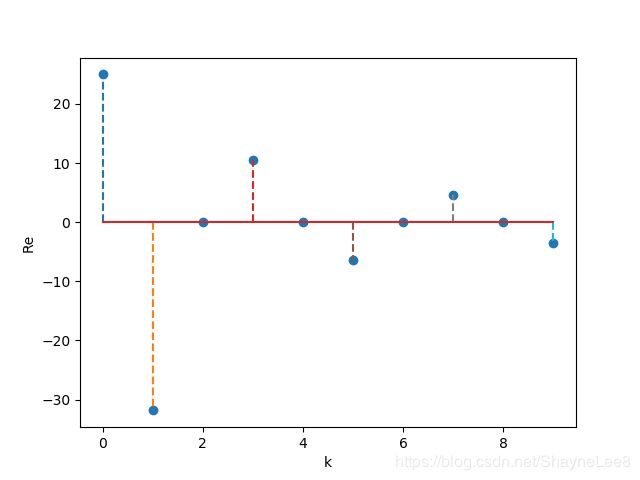
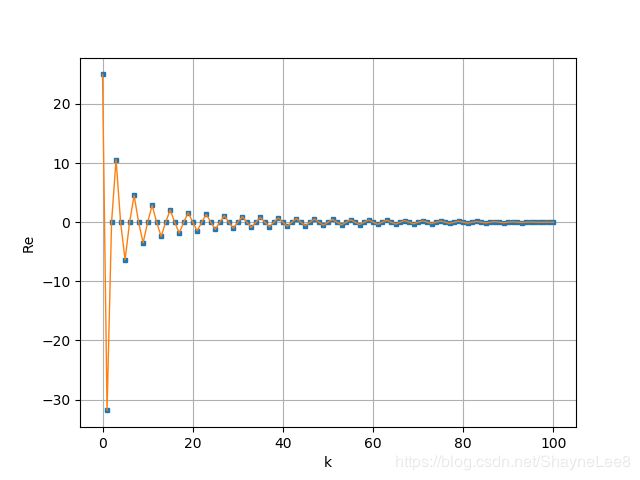
还是先来看刚才前10条曲线的频谱图:
这个图和大家学过的书本上的图很类似,感觉像是体育课上从高到低排列队伍的样子。
还是看不懂?
我开始也是看不懂这个图和前面10条曲线有什么关系, 后来知道变通了,原来这个图是旋转而来的。
怎么转,如下:
旋转结束后,每条曲线的振幅值对应上面的小圆点的值。
全部的101个曲线组成的频谱图如下:
这个看着像啥尼,好像啥也不像 ̄□ ̄||
上面的cos 部分的曲线叠加就说完了。
认真的同学提到了还有sin 部分(在书本上也叫虚部)的曲线没有说。
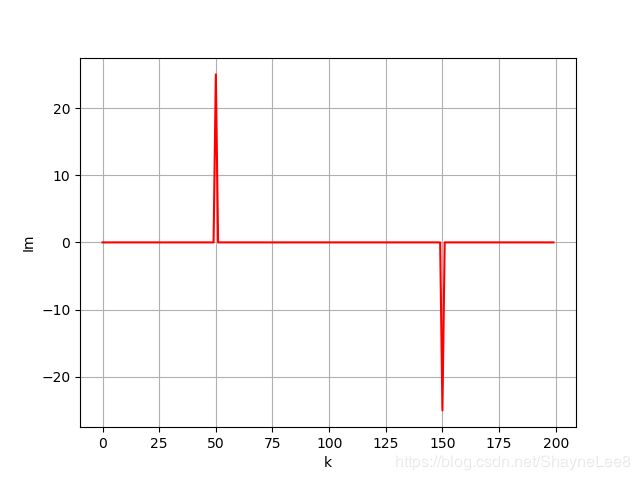
sin 部分不再细讲,只展示结果,其叠加结果如下图:
我也看不出这个有什么作用,好像可有可无,无非和前面实部叠加成的矩形波加起来稍微一点更像矩形。
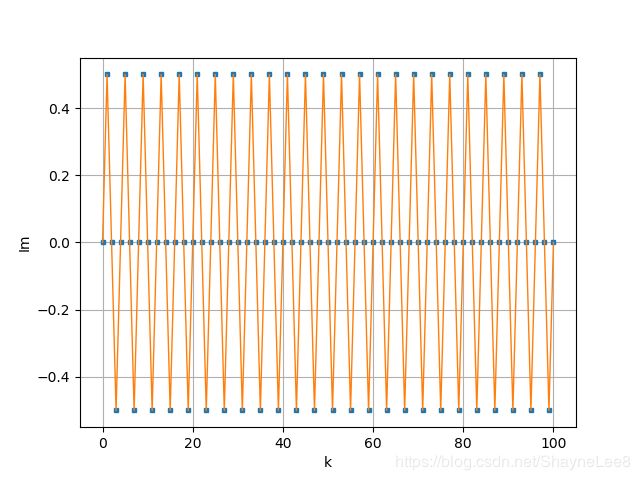
它的频谱图尼是这样子的:
<以上波形图片、动画涉及到的计算方法都是我一行一句用代码写的,如果想看相关的函数计算可以参考参考。有点low,有兴趣的可以去吐槽一下>
代码连接: https://download.csdn.net/download/shaynelee8/10866726 (配合《实用数字信号处理:从原理到应用》作者:StevenW.Smith,第8章:离散傅里叶变换》来看)
最后。
宣布本期节目的问题: 多个正弦波可以叠加成矩形波。 是真的吗?
答案: 是真的!!!