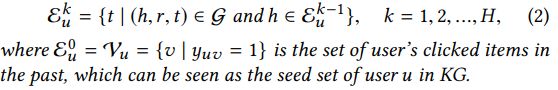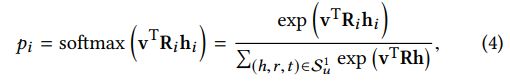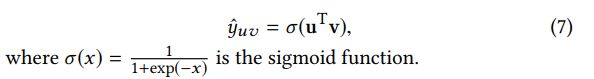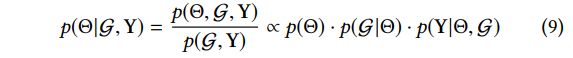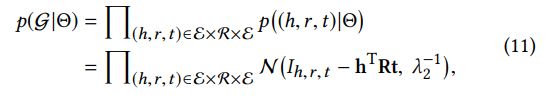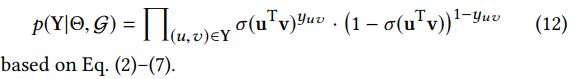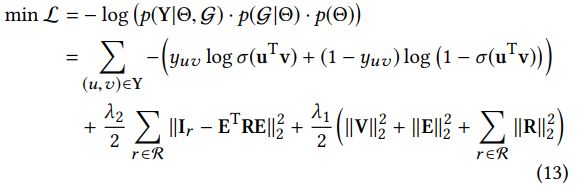阅读笔记--RippleNet: Propagating User Preferences on the Knowledge Graph for Recommender Systems
NLP笔记-- RippleNet
一:概述
将KG作为推荐系统的辅助信息来源,利用实体关系三元组分析用户的偏好倾向并推理出哪些新的实体项可能是该用户可能喜欢的。其中知识图谱即KG指的是由类似(阿甘正传,电影-导演,罗伯特·泽米吉斯)的事实三元组构成,已存在KG,模型输入为:用户![]() 和用户的历史纪录
和用户的历史纪录![]() ,以及项目
,以及项目![]() ;模型输出:用户点击/选择/喜欢该项目的概率。
;模型输出:用户点击/选择/喜欢该项目的概率。
RippleNet背后的关键思想是偏好传播:对于每个用户,RippleNet将其历史兴趣视为KG中的种子集,然后沿着KG链接迭代地扩展用户的兴趣,以发现他对候选项目的等级潜在兴趣。我们将偏好传播与由在水上传播的雨滴产生的实际波纹进行类比,其中多个“波纹”叠加以形成用户在知识图上的最终偏好分布。
二:动机
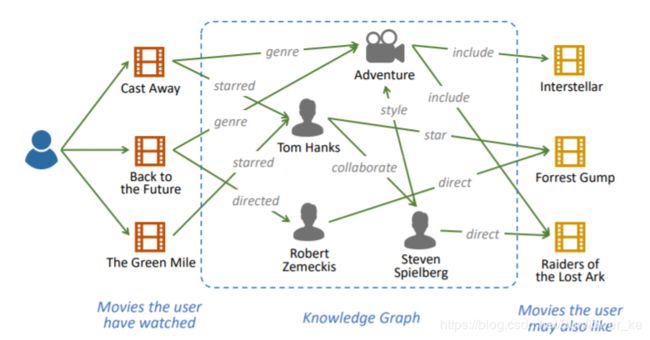
受到KG在各种任务中成功应用的启发,研究人员还尝试利用KG来改善推荐系统的性能。 如图1所示,KG可以从以下三个方面受益:
(1)KG引入项目之间的语义相关性,有助于找到潜在的联系,提高推荐项目的准确性;
(2)KG由各种类型的关系组成,有助于合理地扩展用户的兴趣,增加推荐项目的多样性;
(3)KG连接用户的历史记录和推荐的记录,从而为推荐系统带来可解释性。
图1:知识图谱增强的电影推荐系统的插图。
知识图谱提供了丰富的事实和项目之间的联系,这有助于提高推荐结果的精确性,多样性和可解释性
一般而言,现有的KG感知推荐可分为两类:
第一类是基于嵌入的方法[32,33,43],它使用知识图嵌入(KGE)[35]算法预处理KG,并将学习的实体嵌入合并到推荐框架中。例如,深度知识感知网络(DKN)[33]将实体嵌入和字嵌入视为不同的渠道,然后设计CNN框架将它们组合在一起以进行新闻推荐。协作知识库嵌入(CKE)[43]将CF模块与知识嵌入,文本嵌入和项目的图像嵌入相结合,形成统一的贝叶斯框架。签名异构信息网络嵌入(SHINE)[32]设计深度自动编码器,以嵌入情感网络,社交网络和个人资料(知识)网络,用于名人推荐。基于嵌入的方法在利用KG辅助推荐系统方面表现出很高的灵活性,但这些方法中采用的KGE算法通常更适用于链路预测等图形内应用而不是推荐[35],因此学习实体嵌入更少直观有效地表征项目间关系。
第二类是基于路径的方法[42,45],它探索KG中各项目之间的各种联系模式,为建议提供额外的指导。 例如,个性化实体推荐(PER)[42]和基于元图的推荐[45]将KG视为异构信息网络(HIN),并提取基于元路径/元图的潜在特征来表示用户之间的连接 以及不同类型的关系路径/图表中的项目。 基于路径的方法以更自然和直观的方式使用KG,但它们严重依赖于手动设计的元路径,这在实践中很难优化。 另一个问题是,在实体和关系不在一个域内的某些场景(例如,新闻推荐)中设计手工制作的元路径是不可能的。
为了解决现有方法的局限性,我们提出了RippleNet,一种用于知识图感知推荐的端到端框架。 RippleNet设计用于点击率(CTR)预测,其将用户 - 项目对作为输入并输出用户参与(例如,点击,浏览)项目的概率。 RippleNet背后的关键思想是偏好传播:对于每个用户,RippleNet将其历史兴趣视为KG中的种子集,然后沿着KG链接迭代地扩展用户的兴趣,以发现他对候选项目的等级潜在兴趣。我们将偏好传播与由在水上传播的雨滴产生的实际波纹进行类比,其中多个“波纹”叠加以形成用户在知识图上的最终偏好分布。 RippleNet与现有文献的主要区别在于RippleNet结合了上述两种方法的优点:(1)RippleNet通过偏好传播自然地将KGE方法纳入推荐; (2)RippleNet可以自动发现从用户历史中的项目到候选项目的可能路径,而不需要任何手工设计。
三:贡献
•据我们所知,这是将基于嵌入和基于路径的方法结合到KG感知推荐中的第一项工作。
•我们提出了RippleNet,这是一个利用KG协助推荐系统的端到端框架。 RippleNet通过在KG中迭代传播用户的偏好来自动发现用户的等级潜在兴趣。
•我们对三个真实世界的推荐方案进行了实验,结果证明了RippleNet在几个最先进的基线上的高效。
四:RippleNet模型
在本节中,我们将详细讨论提出的RippleNet。 我们还对模型进行了一些讨论并介绍了相关工作。
4.1框架
RippleNet的框架如图2所示.RippleNet将用户![]() 和项目
和项目![]() 作为输入,并输出用户
作为输入,并输出用户![]() 将点击项目
将点击项目![]() 的预测概率。对于输入用户
的预测概率。对于输入用户![]() ,他的历史兴趣集
,他的历史兴趣集![]() 在KG中被视为种子,然后沿着链接延伸以形成多个波纹组
在KG中被视为种子,然后沿着链接延伸以形成多个波纹组![]() (k=1,2,...k)。一个波纹组
(k=1,2,...k)。一个波纹组![]() 是一组距离种子集
是一组距离种子集![]() 的k-hop的知识三元组集合。 这些波纹集用于迭代地与项目嵌入(黄色块)交互以获得用户
的k-hop的知识三元组集合。 这些波纹集用于迭代地与项目嵌入(黄色块)交互以获得用户![]() 关于项目
关于项目![]() (绿色块)的响应,然后将其组合以形成最终用户嵌入(灰色块)。 最后,我们使用用户
(绿色块)的响应,然后将其组合以形成最终用户嵌入(灰色块)。 最后,我们使用用户![]() 和项
和项![]() 的嵌入来计算预测概率
的嵌入来计算预测概率![]() 。
。
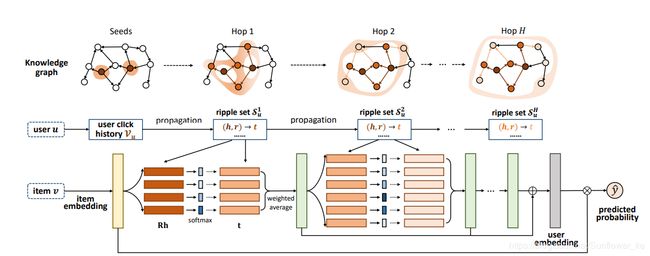
图2:RippleNet的总体框架。 它需要一个用户和一个项目作为输入,并输出用户点击该项目的预测概率。上部的KG示出了由用户的点击历史激活的相应波纹集。
4.2纹波组
知识图通常包含很多事实和实体之间的联系。 例如,如图3所示,电影“Forrest Gump”与“Robert Zemeckis”(导演),“Tom Hanks”(明星),“美国”联系在一起。 (国家)和“Drama”(流派),而“汤姆汉克斯”则与他主演的电影“The terminal”和“Cast Away”联系在一起。这些复杂的联系为我们提供了一个深刻而潜在的视角来探索用户喜好。 例如,如果用户曾经观看过“阿甘正传”,他可能会成为汤姆汉克斯的粉丝并对“The terminal”或“Cast Away”感兴趣。 为了根据KG表征用户的分层扩展偏好,在RippleNet中,我们递归地为用户![]() 定义k-hop相关实体集,如下所示:
定义k-hop相关实体集,如下所示:
定义1(相关实体)。 给定交互矩阵Y和知识图G,用户![]() 的k-hop相关实体集被定义为
的k-hop相关实体集被定义为
相关实体可被视为用户关于KG的历史兴趣的自然延伸。 给定相关实体的定义,然后我们定义用户![]() 的k-hop波纹集如下:
的k-hop波纹集如下:
定义2(纹波集)。用户![]() 的k-hop纹波集被定义为从
的k-hop纹波集被定义为从![]() 开始的知识三元组
开始的知识三元组
“波纹”这个词有两个含义:(1)类似于由多个雨滴创造的真实涟漪,用户对实体的潜在兴趣由他的历史偏好激活,然后沿着KG的链接逐层传播,从近到远。 我们通过图3中所示的同心圆来模拟类比。(2)用户在纹波集中的潜在偏好的强度随着hop数量k的增加而减弱,这类似于实际波纹的逐渐衰减的幅度。图3中的淡蓝色表示中心和周围实体之间的相关性降低。
关于纹波集的一个问题是它们的大小可能随着hop数k的增加而变得太大。为了解决这个问题,请注意:(1)真实KG中的大量实体是sink实体,这意味着它们只有传入链接但没有传出链接,如图3中的“2004”和“PG-13”。 (2)在诸如电影或书籍推荐的特定推荐场景中,关系可以限于与场景相关的类别,以减小波纹集的大小并提高实体之间的相关性。例如,在图3中,所有关系都与电影有关,并且在其名称中包含单词“film”。 (3)最大hop数H在实践中通常不会太大,因为距离用户历史太远的实体可能带来比positive signal还要多的噪声。我们将在实验部分讨论H的选择。 (4)在RippleNet中,我们可以采样固定大小的邻居集,而不是使用完整的纹波集以此来减少计算开销。设计这样的采样器是未来工作的重要方向,尤其是非均匀采样器,以便更好地捕获用户的hierarchical潜在兴趣。
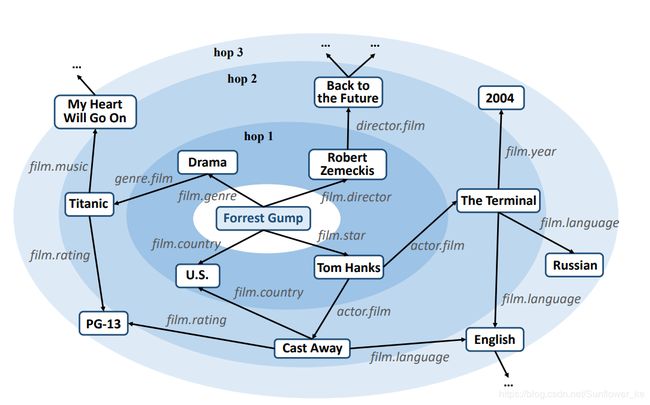
图3:电影KG中“Forrest Gump”波纹组的图示
同心圆表示具有不同跳跃的波纹组。 淡蓝色表示中心与周围实体之间的相关性降低。
请注意,不同hops的波纹组在实践中不一定是不相交的。
4.3偏好传播
如图2所示,每个项目![]() 与项目嵌入v∈
与项目嵌入v∈![]() 相关联,其中d是嵌入的维度。 项目嵌入可以基于应用场景包含项目的one-hot ID [11],属性[32],bag-of-words [33]或上下文信息[25]。 给定项目嵌入
相关联,其中d是嵌入的维度。 项目嵌入可以基于应用场景包含项目的one-hot ID [11],属性[32],bag-of-words [33]或上下文信息[25]。 给定项目嵌入![]() 和用户u的1-hop纹波集合
和用户u的1-hop纹波集合![]() ,通过将项目v与头部hi
,通过将项目v与头部hi![]() 和关系
和关系![]() 进行比较,为
进行比较,为![]() 中的每个三元组(
中的每个三元组(![]() )分配一个关联概率:
)分配一个关联概率:
其中![]() 和
和![]() 分别是关系
分别是关系![]() 和head
和head![]() 的嵌入。 相关概率
的嵌入。 相关概率![]() 可以被视为在关系
可以被视为在关系![]() 的空间中测量的项v和实体
的空间中测量的项v和实体![]() 的相似性。 注意,在计算项目v和实体
的相似性。 注意,在计算项目v和实体![]() 的相关性时,有必要考虑嵌入矩阵
的相关性时,有必要考虑嵌入矩阵![]() ,因为项目 - 实体对在通过不同关系测量时可具有不同的相似性。 例如,“Forrest Gump”和“Cast Away”在考虑他们的导演或明星时非常相似,但如果按流派或作家来衡量,则没有共同之处
,因为项目 - 实体对在通过不同关系测量时可具有不同的相似性。 例如,“Forrest Gump”和“Cast Away”在考虑他们的导演或明星时非常相似,但如果按流派或作家来衡量,则没有共同之处
在获得相关概率之后,我们将![]() 加权中的尾部之和乘以相应的相关概率,并返回向量
加权中的尾部之和乘以相应的相关概率,并返回向量![]() :
:
其中![]() 是尾部
是尾部![]() 的嵌入。向量
的嵌入。向量![]() 可以看作是用户点击历史
可以看作是用户点击历史![]() 相对于项目 v的1-order响应。这类似于基于项目的CF方法[11,33],其中用户由他的相关项而不是 独立的特征向量,以减少参数的大小。 通过方程式(4),(5)中的操作,用户的兴趣从他的历史集合
相对于项目 v的1-order响应。这类似于基于项目的CF方法[11,33],其中用户由他的相关项而不是 独立的特征向量,以减少参数的大小。 通过方程式(4),(5)中的操作,用户的兴趣从他的历史集合![]() 沿着
沿着![]() 中的链路转移到他的1-hop相关实体
中的链路转移到他的1-hop相关实体![]() 的集合,这在RippleNet中称为偏好传播。
的集合,这在RippleNet中称为偏好传播。
请注意,通过在等式(4)中将v替换为![]() ,我们可以重复偏好传播的过程来获得用户u的2阶响应
,我们可以重复偏好传播的过程来获得用户u的2阶响应![]() ,并且可以在用户u的纹波集
,并且可以在用户u的纹波集![]() 上迭代地执行该过程,其中i = 1,...,H。 因此,用户的偏好会远离他的点击历史传播到H-hops,并且我们观察到用户u的多个响应具有不同的顺序:
上迭代地执行该过程,其中i = 1,...,H。 因此,用户的偏好会远离他的点击历史传播到H-hops,并且我们观察到用户u的多个响应具有不同的顺序:![]() 。 通过组合所有order的响应来计算用户u关于项目v的嵌入:
。 通过组合所有order的响应来计算用户u关于项目v的嵌入:
注意,虽然最后一跳的用户响应ouH![]() 理论上包含来自先前跳的所有信息,但仍然需要在计算用户嵌入时合并
理论上包含来自先前跳的所有信息,但仍然需要在计算用户嵌入时合并![]() 小hops k,因为它们在
小hops k,因为它们在![]() 可能是稀疏的。 最后,组合用户嵌入和项目嵌入以输出预测的点击概率:
可能是稀疏的。 最后,组合用户嵌入和项目嵌入以输出预测的点击概率:
4.4学习算法
在RippleNet中,我们打算在观察知识图G和隐式反馈矩阵Y后,最大化以下模型参数Θ的后验概率:
其中Θ包括所有实体,关系和项目的嵌入。 这相当于最大化
根据贝叶斯定理。 在(9),第一个term p(Θ)测量模型参数Θ的先验概率。 根据[43],我们将p(Θ)设置为具有零均值和对角协方差矩阵的高斯分布:
方程式(9)中的第二项是给定Θ的观察知识图G的似然函数。 最近,研究人员提出了许多知识图嵌入方法,包括平移距离模型[3,14]和语义匹配模型[15,19](我们将继续讨论第3.6.3节中的KGE方法)。 在RippleNet中,我们使用three-way张量分解方法来定义KGE的似然函数:
其中如果(h,r,t)∈G指标![]() 等于1,否则为0。 基于方程式(11)中的定义,因此可以在相同的计算模型下统一KGE中的实体-实体对和偏好传播中的项目 - 实体对的评分函数。 方程式(9)中的最后一个项是给定Θ和KG的观察隐式反馈的似然函数,KG被定义为伯努利分布的乘积:
等于1,否则为0。 基于方程式(11)中的定义,因此可以在相同的计算模型下统一KGE中的实体-实体对和偏好传播中的项目 - 实体对的评分函数。 方程式(9)中的最后一个项是给定Θ和KG的观察隐式反馈的似然函数,KG被定义为伯努利分布的乘积:
取方程(9)的负对数。我们对RippleNet有以下损失函数:
其中V和E分别是所有项和实体的嵌入矩阵,Ir![]() 是KG中关系r的张量I的切片,R是关系r的嵌入矩阵。在方程(13)中,第一项测量交互Y的ground truth与RippleNet的预测值之间的交叉熵损失,第二项测量KG
是KG中关系r的张量I的切片,R是关系r的嵌入矩阵。在方程(13)中,第一项测量交互Y的ground truth与RippleNet的预测值之间的交叉熵损失,第二项测量KG ![]() 的ground truth与重建的指标矩阵
的ground truth与重建的指标矩阵![]() 之间的平方误差,以及第三个项是防止过度拟合的正则化项。
之间的平方误差,以及第三个项是防止过度拟合的正则化项。
直接解决上述问题是难以处理的,因此,我们采用随机梯度下降(SGD)算法来迭代地优化损失函数。 RippleNet的学习算法在算法1中给出。在每次训练迭代中,为了使计算更有效,我们采用[16]中负采样策略随机采样来自Y的正/负相互作用的小批量和来自G的真/假三元组。 。然后,我们计算损失L相对于模型参数Θ的梯度,并基于采样minibatch通过反向传播更新所有参数。我们将讨论实验部分中超参数的选择.
4.5讨论
4.5.1可解释性。可解释的推荐系统[27]旨在揭示用户可能喜欢特定项目的原因,这有助于提高他们对推荐的接受度或满意度,并增加对RS的信任。解释通常基于社区标签[29],社交网络[23],方面[2]和短语情绪[44]由于RippleNet基于KG探索用户的兴趣,它通过跟踪从用户的历史到KG中具有高相关概率的项目的路径(等式14),提供了可解释性的新观点。例如,如果在用户1-hop和2-hop上,项目“Back to the future “与 “Forrest Gump”和”Robert Zemeckis”有很高相关概率,那么用户对电影“Back to the Future”的偏好也许可以被这么一条路径解释user watchedForrest Gumpdirected byRobert ZemeckisdirectsBack to the Future![]() 。请注意,与基于路径的方法[42,45]不同,其中路径的模式是手动的,RippleNet根据相关概率自动发现可能的解释路径。我们将在实验部分进一步提供一个可视化的例子,以直观地展示RippleN的可解释性
。请注意,与基于路径的方法[42,45]不同,其中路径的模式是手动的,RippleNet根据相关概率自动发现可能的解释路径。我们将在实验部分进一步提供一个可视化的例子,以直观地展示RippleN的可解释性
4.5.2纹波叠加。 RippleNet中的一个普遍现象是用户的纹波集可能很大,这在偏好传播中不可避免地削弱了他的潜在兴趣。但是,我们发现用户点击历史记录中不同项目的相关实体经常高度重叠。换句话说,从用户的点击历史开始,KG中有多个路径可以到达实体。例如,“Saving Private Ryan”与观看了“The Terminal”,“Jurassic Park”和“Braveheart”的用户,分别通过演员“Tom Hanks”,导演“Steven Spielberg”和类型“War” 相联系。这些并行路径极大地增加了用户对重叠实体的兴趣。我们将这种情况称为纹波叠加,因为它类似于物理中的干涉现象,其中两个波叠加在特定区域中形成更大幅度的合成波。纹波叠加现象在图2中的第二个KG中说明,其中两个较低中间实体周围的较暗红色表示较高用户可能感兴趣的强度。我们还将讨论实验中的纹波叠加