OpenCV-Python (官方)中文教程(部分二)

[部分一]见:https://mp.csdn.net/postedit/103956799

第五章.特征提取与描述

29.理解图像特征

大多数人都玩过拼图游戏。首先你们拿到一张图片的一堆碎片,要做的就是把这些碎片以正确的方式排列起来从而重建这幅图像。问题是怎样做到呢？如果把做游戏的原理写成计算机程序,那计算机就也会玩拼图游戏了。如果计算机可以玩拼图,我们就可以给计算机一大堆自然图片, 然后就可以让计算机把它拼成一张大图了。如果计算机可以自动拼接自然图片, 那我们是不是可以给计算机关于一个建筑的的大量图片,然后让计算机给我们创建一个3D 的的模型呢？问题和联想可以无边无际。但是所有的这些问题都是建立在一个基础问题之上的。这个问题就是：我们是如何玩拼图的？我们是如何把一堆碎片拼在一 起的？我们有时如何把一个个自然场景拼接成一个单独图像的？答案就是：我们要寻找一些唯一的特征,这些特征要适于被跟踪,容易被比较。如果我们要定义这样一种特征,虽然我们知道它是什么但很难用语言来描述。如果让你找出一个可以在不同图片之间相互比较的好的特征,你肯定能搞定。这就是为什么小孩子也会玩拼图的原因。我们在一副图像中搜索这样的特征,我们能找到它们,而且也能在其它图像中找到这些特征,然后再把它们拼接到一块（在拼图游戏中,我们更注重的是图片之间的连续性）。我们的这些能力都是天生的。

所以我们的一个问题现在扩展成了几个,但是更加确切了。这些特征是什么呢？（我们的答案必须也能被计算机理解）。很难说人是怎样找出这些特征的。如果我们深入的观察一些图像并搜索不同的 pattern,我们会发现一 些有趣的事。以下图为例：

图像很简单。在图像的上方给出了六个小图。你要做的就是找到这些小图 在原始图像中的位置。你能找到多少正确结果呢？

A 和 B 是平面,而且它们的图像中很多地方都存在。很难找到这些小图的 准确位置。C 和 D 更简单。它们是建筑的边缘。你可以找到它们的近似位置,但是准确位置还是很难找到。这是因为：沿着边缘,所有的地方都一样。所以边缘是比平面更好的特征,但是还不够好（在拼图游戏中要找连续的边缘）。最后 E 和 F 是建筑的一些角点。它们能很容易的被找到。因为在角点的地方,无论你向哪个方向移动小图,结果都会有很大的不同。所以可以把它们当 成一个好的特征。为了更好的理解这个概念我们举个更简单的例子。

如上图所示,蓝色框中的区域是一个平面很难被找到和跟踪。无论你向哪个方向移动蓝色框,长的都一样。对于黑色框中的区域,它是一个边缘。如果你沿垂直方向移动,它会改变。但是如果沿水平方向移动就不会改变。而红色框中的角点,无论你向那个方向移动,得到的结果都不同,这说明它是唯一的。 所以,基本上来说角点是一个好的图像特征。（不仅仅是角点,有些情况斑点也 是好的图像特征）。

现在我们终于回答了前面的问题了,“这些特征是什么？”。但是下一个问题又来了。我们怎样找到它们？或者说我们怎样找到角点？我们也已经用一种直观的方式做了回答,比如在图像中找一些区域,无论你想那个方向移动这些区域变化都很大。在下一节中我们会用计算机语言来实现这个想法。所以找到图像特征的技术被称为特征检测。

现在我们找到了图像特征（假设你已经搞定）。在找到这些之后,你应该在其它图像中也找到同样的特征。我们应该怎么做呢？我们选择特征周围的一个区域,然后用我们自己的语言来描述它,比如“上边是蓝天,下边是建筑,在建筑上有很多玻璃等”,你就可以在其它图片中搜索相同的区域了。基本上看来, 你是在描述特征。同样,计算机也要对特征周围的区域进行描述,这样它才能 在其它图像中找到相同的特征。我们把这种描述称为特征描述。当你有了特征 很它们的描述后,你就可以在所有的图像中找这个相同的特征了,找到之后你就可以做任何你想做的了。

本章我们就是要使用 OpenCV 中的各种算法来查找图像的特征,然后描 述它们,对它们进行匹配等。

30.Harris 角点检测

在上一章中，我们看到角是图像中各个方向上强度变化较大的区域。

Chris_Harris 和 Mike_Stephens 早在 1988 年的文章《A Combined Corner and Edge Detector》 中就已经提出了角点检测的方法, 被称为 Harris 角点检测。它把这个简单的想法转换成了数学形式。将窗口向各个方向移动（u,v）然后计算所有差异的总和。表达式如下：

窗口函数可以是正常的矩形窗口也可以是对每一个像素给予不同权重的高斯窗口。

角点检测中要使 E (µ, ν) 的值最大。这就是说必须使方程右侧的第二项的 取值最大。对上面的等式进行泰勒级数展开然后再通过几步数学换算（可以参 考其它标准教材）,我们得到下面的等式：

其中

这里 Ix 和 Iy 是图像在 x 和 y 方向的导数。（可以使用函数 cv2.Sobel()计算得到）。

在这之后，它们创建了一个分数，基本上是一个等式，它将决定一个窗口是否可以包含一个角:

其中

• det (M ) = λ1λ2
• trace (M ) = λ1 + λ2

• λ1 和 λ2 是矩阵 M 的特征值

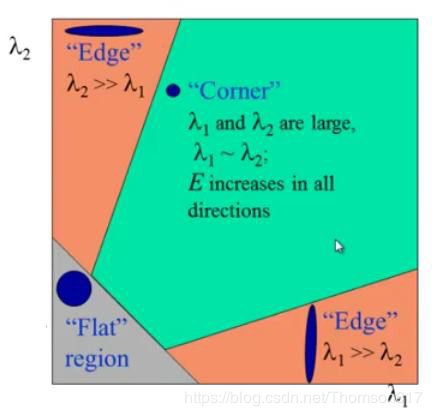
所以根据这些特征中我们可以判断一个区域是否是角点,边界或者是平面。

• 当 λ1 和 λ2 都小时,|R| 也小,这个区域就是一个平坦区域。

• 当 λ1≫ λ2 或者 λ1≪ λ2,时 R 小于 0,这个区域是边缘

• 当 λ1 和 λ2 都很大,并且 λ1～λ2 中的时,R 也很大,（λ1 和 λ2 中的最 小值都大于阈值）说明这个区域是角点。

可以用下图来表示我们的结论：

所以 Harris 角点检测的结果是一个由角点分数构成的灰度图像。选取适 当的阈值对结果图像进行二值化我们就检测到了图像中的角点。我们将用一个简单的图片来演示一下。

30.1 OpenCV 中的 Harris 角点检测

OpenCV  中的函数cv2.cornerHarris() 可以用来进行角点检测。参数如下：

• img - 数据类型为 float32 的输入图像。

•  blockSize  - 角点检测中要考虑的领域大小。

• ksize - Sobel 求导中使用的窗口大小

• k - Harris 角点检测方程中的自由参数,取值参数为 [0,04,0.06].

例子如下：

import cv2
import numpy as np

filename = 'chessboard.jpg' 
img = cv2.imread(filename)
gray = cv2.cvtColor(img,cv2.COLOR_BGR2GRAY) 
gray = np.float32(gray)
# 输入图像必须是  float32,最后一个参数在  0.04 到  0.05 之间
dst = cv2.cornerHarris(gray,2,3,0.04)

#result is dilated for marking the corners, not important
dst = cv2.dilate(dst,None)

# Threshold for an optimal value, it may vary depending on the image.
img[dst>0.01*dst.max()]=[0,0,255]

cv2.imshow('dst',img)
if cv2.waitKey(0) & 0xff == 27: 
    cv2.destroyAllWindows()

结果如下：

30.2 亚像素级精确度的角点

有时我们需要最大精度的角点检测。OpenCV 为我们提供了函数 cv2.cornerSubPix(), 它可以提供亚像素级别的角点检测。下面是一个例子。首先我们要找到 Harris 角点,然后将角点的重心传给这个函数进行修正。Harris 角点用红色像素标 出,绿色像素是修正后的像素。在使用这个函数是我们要定义一个迭代停止条 件。当迭代次数达到或者精度条件满足后迭代就会停止。我们同样需要定义进 行角点搜索的邻域大小。

import cv2
import numpy as np

filename = 'chessboard2.jpg' 
img = cv2.imread(filename)
gray = cv2.cvtColor(img,cv2.COLOR_BGR2GRAY)
# 查找Harris 角点
gray = np.float32(gray)
dst = cv2.cornerHarris(gray,2,3,0.04) 
dst = cv2.dilate(dst,None)
ret, dst = cv2.threshold(dst,0.01*dst.max(),255,0) 
dst = np.uint8(dst)
# 查找重心
#connectedComponentsWithStats(InputArray image, OutputArray labels, OutputArray stats,OutputArray centroids, int connectivity=8, int ltype=CV_32S)
ret, labels, stats, centroids = cv2.connectedComponentsWithStats(dst)
# 定义停止和细化角点的标准
criteria = (cv2.TERM_CRITERIA_EPS + cv2.TERM_CRITERIA_MAX_ITER, 100, 0.001)
#Python: cv2.cornerSubPix(image, corners, winSize, zeroZone, criteria)
#zeroZone – 搜索区域中间的死区大小的一半，在下面的公式中求和没有完成。它有时用来避免自相关矩阵可能的奇异性。(-1，-1)的值表示没有这样的大小.
# 返回值由角点坐标组成的一个数组（而非图像）
corners = cv2.cornerSubPix(gray,np.float32(centroids),(5,5),(-1,-1),criteria)
# Now draw them
res = np.hstack((centroids,corners))
#np.int0 可以用来省略小数点后面的数字（非四舍五入）。 res = np.int0(res) img[res[:,1],res[:,0]]=[0,0,255]
img[res[:,3],res[:,2]] = [0,255,0]

cv2.imwrite('subpixel5.png',img)

结果如下,为了方便查看我们对角点的部分进行了放大：

 

31.Shi-Tomasi角点检测 & 适合于跟踪的图像特征

上一节我们学习了 Harris 角点检测,后来 1994 年,J.Shi 和 C.Tomasi 在它们的文章《Good_Features_to_Track》中对这个算法做了一个小小的修改,并得到了更好的结果。我们知道  Harris  角点检测的打分公式为：

但 Shi-Tomasi 使用的打分函数为：

    R = min (λ1, λ2)

如果打分超过阈值,我们就认为它是一个角点。我们可以把它绘制到 λ1 ～λ2  空间中,就会得到下图：

从这幅图中,我们可以看出来只有当 λ1 和 λ2 都大于最小值时,才被认为是角点（绿色区域）。

OpenCV 提供了函数：cv2.goodFeaturesToTrack()。这个函数可以帮我们使用 Shi-Tomasi 方法获取图像中 N 个最好的角点（也可以通过改变参数来使用 Harris 角点检测算法）。通常情况下,输入的应该 是灰度图像。然后确定你想要检测到的角点数目。再设置角点的质量水平在0 到 1 之间。它代表了角点的最低质量,低于这个数的所有角点都会被忽略。最后在设置两个角点之间的最短欧式距离。

根据这些信息,函数就能在图像上找到角点。所有低于质量水平的角点都会被忽略。然后再把合格角点按角点质量进行降序排列。函数会采用角点质量 最高的那个角点（排序后的第一个）,然后将它附近（最小距离之内）的角点都 删掉。按着这样的方式最后返回 N  个最佳角点。在下面的例子中,我们试着找出 25个最佳角点：

import numpy as np 
import cv2
from matplotlib import pyplot as plt

img = cv2.imread('simple.jpg')
gray = cv2.cvtColor(img,cv2.COLOR_BGR2GRAY)
corners = cv2.goodFeaturesToTrack(gray,25,0.01,10)
# 返回的结果是  [[ 311.,  250.]] 两层括号的数组。
corners = np.int0(corners)
for i in corners: x,y = i.ravel()
cv2.circle(img,(x,y),3,255,-1) 
plt.imshow(img),plt.show()

结果如下：

我们以后会发现这个函数很适合在目标跟踪中使用。

32.SIFT(尺度不变特征变换)介绍

32.1原理

在前面两节我们学习了一些角点检测技术,比如 Harris 等。它们具有旋 转不变特性,即使图片发生了旋转,我们也能找到同样的角点。很明显即使图 像发生旋转之后角点还是角点。那如果我们对图像进行缩放呢？角点可能就不 再是角点了。以下图为例,在一副小图中使用一个小的窗口可以检测到一个角 点,但是如果图像被放大,再使用同样的窗口就检测不到角点了。

所以在 2004 年,D.Lowe 提出了一个新的算法： 尺度不变特征变换（SIFT,Scale-Invariant Feature Transform）,这个算法可以帮助我们提取图像中的关键点并计算它们的描述符。SIFT  算法主要由四步构成。我们来逐步进行学习。

(1).尺度空间极值检测

从上图我们可以很明显的看出来在不同的尺度空间不能使用相同的窗口检测极值点。对小的角点要用小的窗口,对大的角点只能使用大的窗口。为了达到这个目的,我们要使用尺度空间滤波器（尺度空间滤波器可以使用一些列具有不同方差 σ  的高斯卷积核构成）。使用具有不同方差值  σ 的高斯拉普拉斯算子（LoG）对图像进行卷积,LoG 由于具有不同的方差值 σ 所以可以用来检测不同大小的斑点（当 LoG 的方差 σ 与斑点直径相等时能够使斑点完全平滑）。简单来说方差 σ 就是一个尺度变换因子。例如,上图中使用一个小方差 σ 的高斯卷积核是可以很好的检测出小的角点,而使用大方差 σ 的高斯卷积核时可以很 好的检测除大的角点。所以我们可以在尺度空间和二维平面中检测到局部最大值,如（x,y,σ）, 这表示在 σ 尺度中（x,y）点可能是一个关键点。（高斯方差的大小与窗口的大小存在一个倍数关系：窗口大小等于 6 倍方差加 1,所以方差的大小也决定了窗口大小）

但是这个 LoG 的计算量非常大, 所以 SIFT 算法使用高斯差分算子（DoG）来对  LoG   做近似。这里需要再解释一下图像金字塔,我们可以通过减少采样（如只取奇数行或奇数列）来构成一组图像尺寸（1,0.5,0.25 等）不同的金字塔,然后对这一组图像中的每一张图像使用具有不同方差 σ 的高斯卷 积核构建出具有不同分辨率的图像金字塔（不同的尺度空间）。DoG 就是这组具有不同分辨率的图像金字塔中相邻的两层之间的差值。如下图所示：

在 DoG 搞定之后,就可以在不同的尺度空间和 2D 平面中搜索局部最大 值了。对于图像中的一个像素点而言,它需要与自己周围的 8 邻域,以及尺度 空间中上下两层中的相邻的 18（2x9）个点相比。如果是局部最大值,它就可 能是一个关键点。基本上来说关键点是图像在相应尺度空间中的最好代表。如 下图所示：

该算法的作者在文章中给出了 SIFT 参数的经验值：octaves=4（通过 降低采样从而减小图像尺寸,构成尺寸减小的图像金字塔（4 层）？）,尺度空间 为 5,也就是每个尺寸使用 5 个不同方差的高斯核进行卷积,初始方差是 1.6, k  等于  √2 等。

(2).关键点（极值点）定位

一旦找到关键点, 我们就要对它们进行修正从而得到更准确的结果。 作者使用尺度空间的泰勒级数展开来获得极值的准确位置,如果极值点的 灰度值小于阈（0.03） 就会被忽略掉。 在 OpenCV 中这种阈值被称为 contrastThreshold。

DoG   算法对边界非常敏感,所以我们必须要把边界去除。前面我们讲的Harris 算法除了可以用于角点检测之外还可以用于检测边界。作者就是使用了同样的思路。作者使用 2x2 的 Hessian 矩阵计算主曲率。从 Harris 角点检测的算法中,我们知道当一个特征值远远大于另外一个特征值时检测到的是边界。所以它们使用了一个简单的函数,如果比例高于阈值（OpenCV 中称为边界阈值）,这个关键点就会被忽略。文章中给出的边界阈值为 10。

所以低对比度的关键点和边界关键点都会被去除掉,剩下的就是关键点了。

(3).为关键点（极值点）指定方向参数

现在我们要为每个关键点赋予一个反向参数,这样它才会具有旋转不变性。获取关键点（所在尺度空间）的邻域,然后计算这个区域的梯度级和方向。 根据计算得到的结果创建一个含有 36 个 bins（每 10 度一个 bin）的方向直方图。（使用当前尺度空间 σ 值的 1.5 倍为方差的圆形高斯窗口和梯度级做权重）。直方图中的峰值为主方向参数,如果其它的任何柱子的高度高于峰值的 80% 被认为是辅方向。这就会在相同尺度空间的相同位置构建除具有不同方 向的关键点。这对于匹配的稳定性会有所帮助。

(4).关键点描述符

新的关键点描述符被创建了。选取与关键点周围一个 16x16 的邻域,把 它分成 16 个 4x4 的小方块,为每个小方块创建一个具有 8 个 bin 的方向直 方图。总共加起来有 128 个 bin。由此组成长为 128 的向量就构成了关键点 描述符。除此之外还要进行几个测量以达到对光照变化,旋转等的稳定性。

(5).关键点匹配

下一步就可以采用关键点特征向量的欧式距离来作为两幅图像中关键点的 相似性判定度量。取第一个图的某个关键点,通过遍历找到第二幅图像中的距 离最近的那个关键点。但有些情况下,第二个距离最近的关键点与第一个距离 最近的关键点靠的太近。这可能是由于噪声等引起的。此时要计算最近距离与 第二近距离的比值。如果比值大于 0.8,就忽略掉。这会去除 90% 的错误匹 配,同时只去除 5% 的正确匹配。如文章所说。

这就是 SIFT 算法的摘要。非常推荐你阅读原始文献,这会加深你对算法 的理解。请记住这个算法是受专利保护的。所以这个算法包含在 OpenCV 中的收费模块中。

32.2 OpenCV 中的 SIFT

从关键点检 测和绘制开始。首先我们要创建对象。我们可以使用不同的参数,这并不是必须的,关于参数的解释可以查看文档。

import cv2
import numpy as np

img = cv2.imread('home.jpg')
gray= cv2.cvtColor(img,cv2.COLOR_BGR2GRAY)

sift = cv2.SIFT()
kp = sift.detect(gray,None)
img=cv2.drawKeypoints(gray,kp) 
cv2.imwrite('sift_keypoints.jpg',img)

函数 sift.detect() 可以在图像中找到关键点。如果你只想在图像中的一个 区域搜索的话,也可以创建一个掩模图像作为参数使用。返回的关键点是一个 带有很多不同属性的特殊结构体,这些属性中包含它的坐标（x,y）,有意义的 邻域大小,确定其方向的角度等。

OpenCV 也提供了绘制关键点的函数：cv2.drawKeyPoints(),它可以 在关键点的部位绘制一个小圆圈。如果你设置参数为 cv2.DRAW_MATCHES_FLAGS_DRAW_RICH_ 就会绘制代表关键点大小的圆圈甚至可以绘制除关键点的方向。

img=cv2.drawKeypoints(gray,kp,flags=cv2.DRAW_MATCHES_FLAGS_DRAW_RICH_KEYPOINTS) 
cv2.imwrite('sift_keypoints.jpg',img)

结果如下：

现在来计算关键点描述符,OpenCV 提供了两种方法:

(1).既然已经找到了关键字，那么可以调用sift.compute()，它根据找到的关键字计算描述符。例如:kp,des = sift.compute(gray，kp)

(2).如果没有找到关键字，可以使用函数sift.detectAndCompute()在单个步骤中直接找到关键字和描述符。

这里我们来看看第二个方法：

sift = cv.xfeatures2d.SIFT_create()
kp, des = sift.detectAndCompute(gray,None)

这里 kp 是一个关键点列表。des 是一个 Numpy 数组,其大小是关键点数目乘以 128。

所以我们得到了关键点和描述符等。现在我们想看看如何在不同图像之间 进行关键点匹配,这就是我们在接下来的章节将要学习的内容。

33.SURF(Speeded-Up Robust Features)介绍

在上一节中我们学习了使用SIFT算法进行关键点检测和描述。但是这种算法的执行速度比较慢,人们需要速度更快的算法。在2006年Bay,H.,Tuytelaars,T.和VanGool,L共同提出了SURF（加速稳健特征）算法。跟它的名字一样,这个算法是加速版的SIFT。

在SIFT中,Lowe在构建尺度空间时使用DoG对LoG进行近似。SURF使用盒子滤波器（box_filter）对LoG进行近似。下图显示了这种近似。在进行卷积计算时可以利用积分图像（积分图像的一大特点是：计算图像中某个窗口内所有像素和时,计算量的大小与窗口大小无关）,是盒子滤波器的一大优点。而且这种计算可以在不同尺度空间同时进行。同样SURF算法计算关键点的尺度和位置是也是依赖与Hessian矩阵行列式的。

为了保证特征矢量具有选装不变形,需要对于每一个特征点分配一个主要方向。需要以特征点为中心,以6s（s为特征点的尺度）为半径的圆形区域内,对图像进行Harr小波相应运算。这样做实际就是对图像进行梯度运算,但是利用积分图像,可以提高计算图像梯度的效率,为了求取主方向值,需哟啊设计一个以方向为中心,张角为60度的扇形滑动窗口,以步长为0.2弧度左右旋转这个滑动窗口,并对窗口内的图像Haar小波的响应值进行累加。主方向为最大的Haar响应累加值对应的方向。在很多应用中根本就不需要旋转不变性,所以没有必要确定它们的方向,如果不计算方向的话,又可以使算法提速。

SURF提供了成为U-SURF的功能,它具有更快的速度,同时保持了对+/-15度旋转的稳定性。OpenCV对这两种模式同样支持,只需要对参数upright进行设置,当upright为0时计算方向,为1时不计算方向,同时速度更快。

生成特征点的特征矢量需要计算图像的Haar小波响应。在一个矩形的区域内,以特征点为中心,沿主方向将20s*20s的图像划分成4*4个子块,每个子块利用尺寸2s的Haar小波模版进行响应计算,然后对响应值进行统计,组成向量v=(∑dx,∑dy,∑|dx|,∑|dy|)。这个描述符的长度为64。降低的维度可以加速计算和匹配,但又能提供更容易区分的特征。为了增加特征点的独特性,SURF还提供了一个加强版128维的特征描述符。当dy大于0和小于0时分别对dx和|dx|的和进行计算,计算dy和|dy|时也进行区分,这样获得特征就会加倍,但又不会增加计算的复杂度。OpenCV同样提供了这种功能,当参数extended设置为1时为128维,当参数为0时为64维,默认情况为128维。

在检测特征点的过程中计算了Hessian矩阵的行列式,与此同时,计算得到了Hessian矩阵的迹,矩阵的迹为对角元素之和。

按照亮度的不同,可以将特征点分为两种,第一种为特征点迹其周围小邻域的亮度比背景区域要亮,Hessian矩阵的迹为正；另外一种为特征点迹其周围小邻域的亮度比背景区域要暗,Hessian矩阵为负值。根据这个特性,首先对两个特征点的Hessian的迹进行比较。如果同号,说明两个特征点具有相同的对比度；如果异号的话,说明两个特征点的对比度不同,放弃特征点之间的后续的相似性度量。

对于两个特征点描述子的相似性度量,我们采用欧式距离进行计算。简单来说SURF算法采用了很多方法来对每一步进行优化从而提高速度。

分析显示在结果效果相当的情况下SURF的速度是SIFT的3倍。SURF善于处理具有模糊和旋转的图像,但是不善于处理视角变化和关照变化。

OpenCV中的SURF:

与SIFT相同OpenCV也提供了SURF的相关函数。首先我们要初始化一个SURF对象,同时设置好可选参数：64/128维描述符,Upright/Normal模式等。所有的细节都已经在文档中解释的很明白了。就像我们在SIFT中一样,我们可以使用函数SURF.detect(),SURF.compute()等来进行关键点搀着和描述。

首先从查找描述绘制关键点开始。由于和SIFT一样所以我们的示例都在Python终端中演示。

img = cv.imread('fly.png',0)
# 创建SURF对象。您可以在这里或稍后指定参数。这里将Hessian阈值设置为400
surf = cv.xfeatures2d.SURF_create(400)
# 直接查找关键字和描述符
kp, des = surf.detectAndCompute(img,None)
print(len(kp))  # 699

在一幅图像中显示699个关键点太多了。我们把它缩减到50个再绘制到图片上。在匹配时,我们可能需要所有的这些特征,不过现在还不需要。所以我们现在提高Hessian的阈值。

# 检查当前Hessian阀值
print( surf.getHessianThreshold() )    # 400.0

# 我们把它定在50000左右。记住，它只是用来表示图像的。在实际情况中，值最好是300-500
surf.setHessianThreshold(50000)
# 再次计算关键点并检查它的编号.
kp, des = surf.detectAndCompute(img,None)
print( len(kp) )    # 47

现在低于50了,把它们绘制到图像中吧。

img2 = cv.drawKeypoints(img,kp,None,(255,0,0),4)
plt.imshow(img2),plt.show()

结果如下。你会发现SURF很像一个斑点检测器。它可以检测到蝴蝶翅膀上的白班。你可以在其它图片中测试一下。

现在我们试一下U-SURF,它不会检测关键点的方向。

# 检查upright标志，如果它是False，设置为True
print( surf.getUpright() )    #False

surf.setUpright(True)
# 重新计算特征点并绘制它
kp = surf.detect(img,None)
img2 = cv.drawKeypoints(img,kp,None,(255,0,0),4)
plt.imshow(img2),plt.show()

结果如下。所有的关键点的朝向都是一致的。它比前面的快很多。如果你的工作对关键点的朝向没有特别的要求（如全景图拼接）等,这种方法会更快。

最后我们再看看关键点描述符的大小,如果是64维的就改成128维。

# 查找描述符的大小
print( surf.descriptorSize() )    # 64
# 这意味着"extended"为False.
surf.getExtended()    # False
# 所以我们将其设置成True得到128个模糊描述符.
surf.setExtended(True)
kp, des = surf.detectAndCompute(img,None)
print( surf.descriptorSize() )    # 128
print( des.shape )    # (47, 128)

接下来要做的就是匹配了,我们会在后面讨论。

34.角点检测的FAST算法

我们前面学习了几个特征检测器,它们大多数效果都很好。但是从实时处理的角度来看,这些算法都不够快。一个最好例子就是SLAM（同步定位与地图构建）,移动机器人,它们的计算资源非常有限。为了解决这个问题,Edward_Rosten和Tom_Drummond在2006年提出里FAST算法。我们下面将会对此算法进行一个简单的介绍。你可以参考原始文献获得更多细节。

34.1使用FAST算法进行特征提取

1.在图像中选取一个像素点p,来判断它是不是关键点。Ip等于像素点p的灰度值。

2.选择适当的阈值t。

3.如下图所示在像素点p的周围选择16个像素点进行测试。

4.如果在这16个像素点中存在n个连续像素点的灰度值都高于Ip+t,或者低于Ip−t,那么像素点p就被认为是一个角点。如上图中的虚线所示,n选取的值为12。

5.为了获得更快的效果,还采用了而外的加速办法。首先对候选点的周围每个90度的点：1,9,5,13进行测试（先测试1和19,如果它们符合阈值要求再测试5和13）。如果p是角点,那么这四个点中至少有3个要符合阈值要求。如果不是的话肯定不是角点,就放弃。对通过这步测试的点再继续进行测试（是否有12的点符合阈值要求）。这个检测器的效率很高,但是它有如下几条缺点：

•当n<12时它不会丢弃很多候选点(获得的候选点比较多)。

•像素的选取不是最优的,因为它的效果取决与要解决的问题和角点的分布情况。

•高速测试的结果被抛弃

•检测到的很多特征点都是连在一起的。

前3个问题可以通过机器学习的方法解决,最后一个问题可以使用非最大值抑制的方法解决。

34.2机器学习的角点检测器

1.选择一组训练图片（最好是跟最后应用相关的图片）

2.使用FAST算法找出每幅图像的特征点

3.对每一个特征点,将其周围的16个像素存储构成一个向量。对所有图像都这样做构建一个特征向量P

4.每一个特征点的16像素点都属于下列三类中的一种。

5.根据这些像素点的分类,特征向量P也被分为3个子集：Pd,Ps,Pb

6.定义一个新的布尔变量Kp,如果p是角点就设置为Ture,如果不是就设置为False.

7.使用ID3算法（决策树分类器）查询每个子集，使用变量Kp查询关于真类的知识。它选择产生关于候选像素是否是角的最多信息的x，通过Kp的熵来测量。

8.这是递归地应用于所有的子集，直到它的熵为零。

9.将构建好的决策树运用于其它图像的快速的检测。

34.3 非极大值抑制

使用极大值抑制的方法可以解决检测到的特征点相连的问题

1.对所有检测到到特征点构建一个打分函数V。V就是像素点p与周围16个像素点差值的绝对值之和。

2.计算临近两个特征点的打分函数V。

3.忽略V值最低的特征点.

34.4 OpenCV中FAST特征检测器

和其它特征点检测一样,我们可以在OpenCV中直接使用FAST特征检测器。如果你愿意的话,你还可以设置阈值,是否进行非最大值抑制,要使用的邻域大小等。

邻域设置为下列3种之一：

cv2.FAST_FEATURE_DETECTOR_TYPE_5_8;
cv2.FAST_FEATURE_DETECTOR_TYPE_7_12 ;
cv2.FAST_FEATURE_DETECTOR_TYPE_9_16。

下面是使用 FAST 算 法进行特征点检测的简单代码。

import numpy as np
import cv2
from matplotlib import pyplot as plt

img = cv2.imread('simple.jpg', 0)
# Initiate FAST object with default values
fast = cv2.FastFeatureDetector()
# find and draw the keypoints
kp = fast.detect(img, None)
img2 = cv2.drawKeypoints(img, kp, color=(255, 0, 0))
# Print all default params
print("Threshold: ", fast.getInt('threshold'))
print("nonmaxSuppression: ", fast.getBool('nonmaxSuppression'))
print("neighborhood: ", fast.getInt('type'))
print("Total Keypoints with nonmaxSuppression: ", len(kp))
cv2.imwrite('fast_true.png', img2)
# Disable nonmaxSuppression fast.setBool('nonmaxSuppression',0) 
kp = fast.detect(img,None)
print("Total Keypoints without nonmaxSuppression: ", len(kp))
img3 = cv2.drawKeypoints(img, kp, color=(255, 0, 0))
cv2.imwrite('fast_false.png', img3)

结果如下。第一幅图是使用了非最大值抑制的结果,第二幅没有使用非最大值抑制。

FAST 算法比其它角点检测算法都快。 但是在噪声很高时不够稳定,这是由阈值决定。

35.BRIEF(二值稳健的独立补充特征)

我们知道 SIFT 算法使用的是 128 维的描述符。由于它是使用的浮点数, 所以要使用 512 个字节。同样 SURF 算法最少使用 256 个字节（64 为维描 述符）。创建一个包含上千个特征的向量需要消耗大量的内存,在嵌入式等资源 有限的设备上这样是合适的。匹配时还会消耗更多的内存和时间。

但是在实际的匹配过程中如此多的维度是没有必要的。我们可以使用 PCA, LDA 等方法来进行降维。甚至可以使用 LSH（局部敏感哈希）将 SIFT 浮点 数的描述符转换成二进制字符串。对这些字符串再使用汉明距离进行匹配。汉明距离的计算只需要进行 XOR 位运算以及位计数,这种计算很适合在现代的 CPU 上进行。但我们还是要先找到描述符才能使用哈希,这不能解决最初的内存消耗问题。

BRIEF (Binary Robust Independent El-ementary Features)应运而生。它不去计算描述符而是直接找到一个二进制字符串。这 种算法使用的是已经平滑后的图像,它会按照一种特定的方式选取一组像素点 对 nd (x,y),然后在这些像素点对之间进行灰度值对比。例如,第一个点对的 灰度值分别为 p 和 q。如果 p 小于 q,结果就是 1,否则就是 0。就这样对 nd 个点对进行对比得到一个 nd  维的二进制字符串。

nd 可以是 128,256,512。OpenCV 对这些都提供了支持,但在默认 情况下是 256（OpenC 是使用字节表示它们的,所以这些值分别对应与 16, 32,64）。当我们获得这些二进制字符串之后就可以使用汉明距离对它们进行 匹配了。

非常重要的一点是：BRIEF 是一种特征描述符,它不提供查找特征的方法。 所以我们不得不使用其它特征检测器,比如 SIFT 和 SURF 等。原始文献推荐 使用 CenSurE 特征检测器,这种算法很快。而且 BRIEF 算法对 CenSurE 关键点的描述效果要比SURF关键点的描述更好。

简单来说 BRIEF 是一种对特征点描述符计算和匹配的快速方法。这种算 法可以实现很高的识别率,除非出现平面内的大旋转。

OpenCV 中的 BRIEF:

下面的代码使用了 CenSurE  特征检测器和 BRIEF  描述符。（在 OpenCV中 CenSurE 检测器被叫做 STAR 检测器）。

import numpy as np
import cv2
from matplotlib import pyplot as plt

img = cv2.imread('simple.jpg', 0)
# Initiate STAR detector
star = cv2.FeatureDetector_create("STAR")
# Initiate BRIEF extractor
brief = cv2.DescriptorExtractor_create("BRIEF")
# find the keypoints with STAR
kp = star.detect(img, None)
# compute the descriptors with BRIEF
kp, des = brief.compute(img, kp)
print(brief.getInt('bytes'))
print(des.shape)

函数 brief.getInt(′bytes′) 会以字节格式给出 nd 的大小,默认值为 32。下面就是匹配了,我们会在其它章节中介绍。

 

36.ORB(定向快且旋转短的BRIEF)

对于一个 OpenCV  的狂热爱好者来说 ORB(Oriented FAST and Rotated BRIEF)  最重要的一点就是：它来自 “OpenCV_Labs''。这个算法是在 2011 年提出的。在计算开支,匹配效率以 及更主要的是专利问题方面 ORB 算法是 SIFT 和 SURF 算法的一个很好的 替代品。SIFT 和 SURF 算法是有专利保护的,如果你要使用它们,就可能要 花钱。但是 ORB 不需要！！

ORB 基本是 FAST 关键点检测和 BRIEF 关键点描述器的结合体,并通 过很多修改增强了性能。首先它使用 FAST 找到关键点,然后再使用 Harris 角点检测对这些关键点进行排序找到其中的前 N 个点。它也使用金字塔从而产 生尺度不变性特征。但是有一个问题,FAST 算法步计算方向。那旋转不变性 怎样解决呢？作者进行了如下修改。

它使用灰度矩的算法计算出角点的方向。以角点到角点所在（小块）区域 质心的方向为向量的方向。为了进一步提高旋转不变性,要计算以角点为中心 半径为 r 的圆形区域的矩,再根据矩计算除方向。

对于描述符,ORB 使用的是 BRIEF 描述符。但是我们已经知道 BRIEF 对与旋转是不稳定的。所以我们在生成特征前,要把关键点领域的这个 patch 的坐标轴旋转到关键点的方向。对于任意位置(xi, yi)的n个二进制测试的特征集，定义一个2×n的矩阵，S包含这些像素的坐标。然后使用补丁的取向,θ,发现其旋转矩阵和旋转S Sθ带领(旋转)版本。ORB离散化的角增量of2π/ 30(12度),并构造一个查找表的预先计算的简单模式。只要关键点定位\θ是一致的观点,正确的点集Sθ将用于计算它的描述符。

BRIEF 有一个重要的性质，那就是每个位元特徵都有一个大的变异数和一个接近0.5的均值。但是一旦它沿着关键点方向定向，它就会失去这种特性，变得更加分散。由于对输入的响应不同，高方差使特征更具有鉴别性。另一个可取的特性是使测试不相关，因为这样每个测试都有助于结果。为了解决所有这些问题，ORB在所有可能的二进制测试中进行贪婪搜索，以找到方差和平均值都接近0.5且不相关的测试。其结果称为BRIEF。

在描述符匹配中，使用了改进传统LSH的多探针LSH。文章说ORB比SURF和SIFT快得多，而ORB描述符比SURF工作得更好。在低功耗全景拼接等设备中，ORB是一个很好的选择。

实验证明,BRIEF  算法的每一位的均值接近 0.5,并且方差很大。steered_BRIEF

算法的每一位均值比较分散（均值为 0.5,0.45,0.35... 等值的关键点数相当）,这导致方差减小。数据的方差大的一个好处是：使得特征更容易分辨。为了对steered_BRIEF 算法使得特征的方差减小的弥补和减小数据间的相关性, 用一个学习算法（learning      method）选择二进制测试的一个子集。

在描述符匹配中使用了对传统 LSH 改善后的多探针 LSH。文章中说 ORB 算法比 SURF 和 SIFT 算法快的多,ORB 描述符也比 SURF 好很多。ORB 是低功耗设备的最佳选择。

OpenCV中的ORB算法:

和前面一样我们首先要使用函数 cv3.ORB() 或者 feature2d 通用接口 创建一个 ORB 对象。它有几个可选参数。最有用的应该是 nfeature,默认 值为 500,它表示了要保留特征的最大数目。scoreType 设置使用 Harris 打分还是使用 FAST 打分对特征进行排序（默认是使用 Harris 打分）等。参 数 WTA_K 决定了产生每个oriented_BRIEF 描述符要使用的像素点的数目。默认值是 2,也就是一次选择两个点。在这种情况下进行匹配,要使用 NORM_HAMMING 距离。如果 WTA_K 被设置成 3 或 4,那匹配距离就要设置为    NORM_HAMMING2。

下面是一个使用 ORB 的简单代码。

import numpy as np
import cv2
from matplotlib import pyplot as plt

img = cv2.imread('simple.jpg', 0)
# Initiate STAR detector
orb = cv2.ORB()
# find the keypoints with ORB
kp = orb.detect(img, None)
# compute the descriptors with ORB
kp, des = orb.compute(img, kp)
# 只绘制关键点的位置，而不是大小和方向
img2 = cv2.drawKeypoints(img, kp, color=(0, 255, 0), flags=0)
plt.imshow(img2), plt.show()

结果如下：

我们将在其它章节介绍  ORB  特征匹配。

37.特征匹配

37.1 Brute-Force 匹配的基础

蛮力匹配器是很简单的。首先在第一幅图像中选取一个关键点然后依次与 第二幅图像的每个关键点进行（描述符）距离测试,最后返回距离最近的关键 点。

对于 BF 匹配器,我们首先要使用 cv2.BFMatcher() 创建一个 BFMatcher 对象。它有两个可选参数。第一个是 normType。它是用来指定要 使用的距离测试类型。默认值cv2.Norm_L2。这很适合 SIFT 和 SURF 等(cv2.NORM_L1 也可以)。对于使用二进制描述符的 ORB,BRIEF,BRISK 算法等,要使用 cv2.NORM_HAMMING,这样就会返回两个测试对象之 间的汉明距离。如果 ORB 算法的参数设置为 WTA_K==3 或 4,normType 就应该设置成cv2.NORM_HAMMING2。

第二个参数是布尔变量 crossCheck,默认值为 False。如果设置为 True,匹配条件就会更加严格,只有到 A 中的第 i 个特征点与 B 中的第 j 个 特征点距离最近,并且 B 中的第 j 个特征点到 A 中的第 i 个特征点也是最近（A 中没有其它点到 j 的距离更近）时才会返回最佳匹配（i,j）。也就是这两个特征点要互相匹配才行。这样就能提供统一的结果,这可以用来替代 D.Lowe 在 SIFT 文章中提出的比值测试方法。

BFMatcher 对象具有两个方法,BFMatcher.match() 和 BFMatcher.knnMatch()。 第一个方法会返回最佳匹配。第二个方法为每个关键点返回 k  个最佳匹配（降

序排列之后取前 k 个）,其中 k 是由用户设定的。如果除了匹配之外还要做其 它事情的话可能会用上（比如进行比值测试）。就像使用 cv2.drawKeypoints() 绘 制关 键点一样, 我们可以使用 cv2.drawMatches() 来绘制匹配的点。它会将这两幅图像先水平排列,然后 在最佳匹配的点之间绘制直线（从原图像到目标图像）。如果前面使用的是 BF- Matcher.knnMatch(),现在我们可以使用函数 cv2.drawMatchsKnn 为每个关键点和它的 k 个最佳匹配点绘制匹配线。如果 k 等于 2,就会为每个 关键点绘制两条最佳匹配直线。如果我们要选择性绘制话就要给函数传入一个 掩模。

让我们分别看一个 ORB 和一个 SURF 的例子吧。（使用不同距离计算方法）。

(1).对 ORB 描述符进行蛮力匹配

现在我们看一个在两幅图像之间进行特征匹配的简单例子。在本例中我们 有一个查询图像和一个目标图像。我们要使用特征匹配的方法在目标图像中寻 找查询图像的位置。（这两幅图像分别是/sample/c/box.png,和/sample/c/ box_in_scene.png）

我们使用  ORB  描述符来进行特征匹配。首先我们需要加载图像计算描述符。

import numpy as np
import cv2
from matplotlib import pyplot as plt

img1 = cv2.imread('box.png',0) # queryImage
img2 = cv2.imread('box_in_scene.png',0) # trainImage

下面我们要创建一个 BFMatcher 对象,并将距离计算设置为 cv2.NORM_HAMMING(因为我们使用的是 ORB),并将 crossCheck 设置为 True。然后使用 Matcher.match() 方法获得两幅图像的最佳匹配。然后将匹配结果按特征点之间的距离进行降序排列,这样最佳匹配就会排在前面了。最后我们只将前 10 个匹配绘制出来（太多了看不清,如果愿意的话你可以多画几条）。

# Initiate SIFT detector
orb = cv2.ORB()
# find the keypoints and descriptors with SIFT 
kp1, des1 = orb.detectAndCompute(img1,None)
kp2, des2 = orb.detectAndCompute(img2,None)
# create BFMatcher object
bf = cv2.BFMatcher(cv2.NORM_HAMMING, crossCheck=True)
# Match descriptors.
matches = bf.match(des1,des2)
# Sort them in the order of their distance.
matches = sorted(matches, key = lambda x:x.distance)

下面就是我得到的结果。

(2).匹配器对象

matches = bf.match(des1, des2) 返回值是一个 DMatch 对象列表。这个DMatch 对象具有下列属性：

• DMatch.distance - 描述符之间的距离。越小越好。
• DMatch.trainIdx - 目标图像中描述符的索引。
• DMatch.imgIdx - 目标图像的索引。
• DMatch.queryIdx - 查询图像中描述符的索引。

(3).对 SIFT 描述符进行蛮力匹配和比值测试

现在我们使用 BFMatcher.knnMatch() 来获得 k 对最佳匹配。在本例中 我们设置 k = 2,这样我们就可以使用 D.Lowe 文章中的比值测试了。

import numpy as np
import cv2
from matplotlib import pyplot as plt

img1 = cv2.imread('box.png', 0)
img2 = cv2.imread('box_in_scene.png', 0)  # trainImage
# Initiate SIFT detector
sift = cv2.SIFT()
# find the keypoints and descriptors with SIFT 
kp1, des1 = sift.detectAndCompute(img1, None)
kp2, des2 = sift.detectAndCompute(img2, None)
# BFMatcher with default params
bf = cv2.BFMatcher()
matches = bf.knnMatch(des1, des2, k=2)
# Apply ratio test
# 比值测试,首先获取与A 距离最近的点B（最近）和C（次近）,只有当B/C小于阈值时（0.75）才被认为是匹配,因为假设匹配是一一对应的,真正的匹配的理想距离为0
good = []
for m, n in matches:
    if m.distance < 0.75 * n.distance: good.append([m])

# cv2.drawMatchesKnn expects list of lists as matches.
img3 = cv2.drawMatchesKnn(img1, kp1, img2, kp2, good[:10], flags=2)
plt.imshow(img3), plt.show()

结果如下：

37.2 FLANN 匹配器

FLANN 是快速最近邻搜索包（Fast_Library_for_Approximate_Nearest_Neighbors） 的简称。它是一个对大数据集和高维特征进行最近邻搜索的算法的集合,而且 这些算法都已经被优化过了。在面对大数据集时它的效果要好于 BFMatcher。 我们来对第二个例子使用   FLANN  匹配看看它的效果。

使用 FLANN 匹配,需要传入两个字典作为参数。这两个用来确定要使用的算法和其它相关参数等。第一个是 IndexParams。各种不同算法的信 息可以在 FLANN 文档中找到。这里我们总结一下,对于 SIFT 和 SURF 等, 我们可以传入的参数是：

indexparams = dict(algorithm = FLANNI NDEXKDTREE, trees = 5)

但使用 ORB 时,我们要传入的参数如下。注释掉的值是文献中推荐使用 的,但是它们并不适合所有情况,其它值的效果可能会更好。

import numpy as np
import cv2
from matplotlib import pyplot as plt

img1 = cv2.imread('box.png', 0)
img2 = cv2.imread('box_in_scene.png', 0)  # trainImage
# Initiate SIFT detector
sift = cv2.SIFT()
# find the keypoints and descriptors with SIFT 
kp1, des1 = sift.detectAndCompute(img1, None)
kp2, des2 = sift.detectAndCompute(img2, None)
# BFMatcher with default params
bf = cv2.BFMatcher()
matches = bf.knnMatch(des1, des2, k=2)
# Apply ratio test
good = []
for m, n in matches:
    if m.distance < 0.75 * n.distance: good.append([m])

# cv2.drawMatchesKnn expects list of lists as matches.
img3 = cv2.drawMatchesKnn(img1, kp1, img2, kp2, good, flags=2)
plt.imshow(img3), plt.show()

第二个字典是 SearchParams,用它来指定递归遍历的次数,值越高结果越准确, 但是消耗的时间也越多。 如果想修改这个值, 传入参数：searchparams = dict(checks = 100)。

有了这些信息我们就可以开始了。

import numpy as np
import cv2
from matplotlib import pyplot as plt

img1 = cv2.imread('box.png', 0)
img2 = cv2.imread('box_in_scene.png', 0)  # trainImage
# Initiate SIFT detector
sift = cv2.SIFT()
# find the keypoints and descriptors with SIFT 
kp1, des1 = sift.detectAndCompute(img1, None)
kp2, des2 = sift.detectAndCompute(img2, None)
# FLANN parameters
FLANN_INDEX_KDTREE = 0
index_params = dict(algorithm = FLANN_INDEX_KDTREE, trees = 5) 
search_params = dict(checks=50)    # or pass empty dictionary

flann = cv2.FlannBasedMatcher(index_params,search_params) 
matches = flann.knnMatch(des1,des2,k=2)
# Need to draw only good matches, so create a mask
matchesMask = [[0,0] for i in range(len(matches))]
# ratio test as per Lowe's paper
for i,(m,n) in enumerate(matches):
    if m.distance < 0.7*n.distance:
        matchesMask[i]=[1,0]

draw_params = dict(matchColor = (0,255,0),singlePointColor = (255,0,0), matchesMask = matchesMask, flags = 0)
img3 = cv2.drawMatchesKnn(img1,kp1,img2,kp2,matches,None,**draw_params) 
plt.imshow(img3,),plt.show()

结果如下：

38.使用特征匹配和单应性查找对象

联合使用特征提取和 calib3d 模块中的 findHomography 在复杂图像 中查找已知对象。

上一节我们使用一个查询图像,在其中找到一些特征点（关键点）,我们又在另一幅图像中也找到了一些特征点,最后对这两幅图像之间的特征点进行匹配。简单来说就是：我们在一张杂乱的图像中找到了 一个对象（的某些部分）的位置。这些信息足以帮助我们在目标图像中准确找到（查询图像）对象。

为了达到这个目的我们可以使用 calib3d 模块中的 cv2.findHomography() 函数。如果将这两幅图像中的特征点集传给这个函数,它就会找到这个对象的 透视图变换。然后我们就可以使用函数 cv2.perspectiveTransform() 找到这 个对象了。至少要 4 个正确的点才能找到这种变换。

我们已经知道在匹配过程可能会有一些错误,而这些错误会影响最终结果。为了解决这个问题,算法使用 RANSAC 和 LEAST_MEDIAN(可以通过 参数来设定)。所以好的匹配提供的正确的估计被称为 inliers,剩下的被称为 outliers。cv2.findHomography() 返回一个掩模,这个掩模确定了 inlier 和 outlier  点。

和通常一样我们先在图像中来找到 SIFT 特征点,然后再使用比值测试找 到最佳匹配。

import numpy as np
import cv2
from matplotlib import pyplot as plt

img1 = cv2.imread('box.png', 0)
img2 = cv2.imread('box_in_scene.png', 0)  # trainImage
# Initiate SIFT detector
sift = cv2.SIFT()
# find the keypoints and descriptors with SIFT 
kp1, des1 = sift.detectAndCompute(img1, None)
kp2, des2 = sift.detectAndCompute(img2, None)
FLANN_INDEX_KDTREE = 0
index_params = dict(algorithm = FLANN_INDEX_KDTREE, trees = 5) 
search_params = dict(checks = 50)
flann = cv2.FlannBasedMatcher(index_params, search_params) 
matches = flann.knnMatch(des1,des2,k=2)
# store all the good matches as per Lowe's ratio test.
good = []
for m,n in matches:
    if m.distance < 0.7*n.distance: 
        good.append(m)

现在设置只有存在 10 个以上匹配时才去查找目标（MIN_MATCH_COUNT=10）, 否则显示警告消息：“现在匹配不足！”如果找到了足够的匹配, 我们要提取两幅图像中匹配点的坐标, 把它们传入到函数中计算透视变换。一旦我们找到 3x3 的变换矩阵,就可以使用它将查 询图像的四个顶点（四个角）变换到目标图像中去了。然后再绘制出来。

if len(good)>MIN_MATCH_COUNT:
    # 获取关键点的坐标
    src_pts = np.float32([ kp1[m.queryIdx].pt for m in good ]).reshape(-1,1,2) 
    dst_pts = np.float32([ kp2[m.trainIdx].pt for m in good ]).reshape(-1,1,2)
    # 第三个参数  用于计算单应矩阵的方法。以下是可能的方法:
    # 0 - 使用所有点的常规方法
    # CV_RANSAC - RANSAC-based robust method
    # CV_LMEDS - Least-Median robust method
    # 第四个参数取值范围在  1 到 10, 拒绝一个点对的阈值。原图像的点经过变换后点与目标图像上对应点的误差, 超过误差就认为是  outlier
    # 返回值中  M 为变换矩阵。
    M, mask = cv2.findHomography(src_pts, dst_pts, cv2.RANSAC,5.0) 
    matchesMask = mask.ravel().tolist()
    # 获得原图像的高和宽
    h,w = img1.shape
    # 使用得到的变换矩阵对原图像的四个角进行变换,获得在目标图像上对应的坐标。
    pts = np.float32([ [0,0],[0,h-1],[w-1,h-1],[w-1,0] ]).reshape(-1,1,2) 
    dst = cv2.perspectiveTransform(pts,M)
    # 原图像为灰度图
    cv2.polylines(img2,[np.int32(dst)],True,255,10, cv2.LINE_AA)

else:
    print ("Not enough matches are found - %d/%d" % (len(good),MIN_MATCH_COUNT))
    matchesMask = None

最后再绘制 inliers（如果成功找到目标图像）或者匹配关键点（如果失败）。

draw_params = dict(matchColor = (0,255,0), # draw matches in green color
                   singlePointColor = None,
                   matchesMask = matchesMask, # draw only inliers
                   flags = 2)
img3 = cv2.drawMatches(img1,kp1,img2,kp2,good,None,**draw_params)
plt.imshow(img3, 'gray'),plt.show()

结果如下。复杂图像中被找到的目标图像被标记成白色。

 

第六章.视频分析(运动目标检测)

39.Meanshift 和 Camshift

39.1 Meanshift

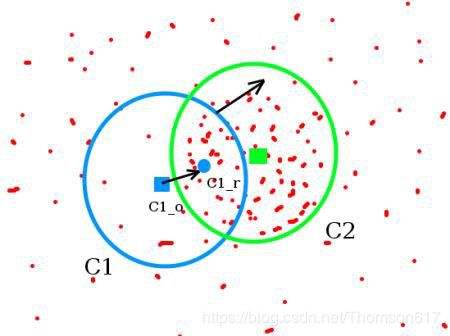
Meanshift(均值偏移) 算法的基本原理很简单。假设我们有一堆点（可以是像直方图反投影那样的像素分布）和一个小窗口(可能是一个圆圈),我们要完成的任务就是将这个窗口移动到最大灰度密度处（或者是点最多的地方）。如下图所示：

 

初始窗口是蓝色“C1”,它的圆心为蓝色方框“C1_o”,而窗口中所有点的质心却是“C1_r” (小的蓝色圆圈),很明显圆心和点的质心没有重合。所以移动圆 心 C1_o  到质心 C1_r,这样我们就得到了一个新的窗口。这时又可以找到新 窗口内所有点的质心,大多数情况下还是不重合的,所以重复上面的操作：将 新窗口的中心移动到新的质心。就这样不停的迭代操作直到窗口的中心和其所 包含点的质心重合为止（或者有一点小误差）。按照这样的操作我们的窗口最终 会落在像素值（和）最大的地方。如上图所示“C2”是窗口的最后位置,可 以看出该窗口中的像素点最多。整个过程如下图所示：

通常情况下我们要使用直方图方向投影得到的图像和目标对象的起始位置。 当目标对象的移动会反映到直方图反向投影图中。就这样,meanshift 算法把窗口移动到图像中灰度密度最大的区域。

 

要在 OpenCV 中使用 Meanshift 算法首先要对目标对象进行设置, 计算目标对象的直方图,这样在执行 meanshift 算法时就可以将目标对象反向投影到每一帧中。另外我们还需要提供窗口的起始位置。在这里我们值计算 H（Hue）通道的直方图,同样为了避免低亮度造成的影响,我们使 用函数  cv2.inRange()  将低亮度的值忽略掉。

import numpy as np 
import cv2

cap = cv2.VideoCapture('slow.flv')
# take first frame of the video
ret,frame = cap.read()
# setup initial location of window
r,h,c,w = 250,90,400,125  # simply hardcoded the values
track_window = (c,r,w,h)
# set up the ROI for tracking
roi = frame[r:r+h, c:c+w]
hsv_roi =  cv2.cvtColor(frame, cv2.COLOR_BGR2HSV)
mask = cv2.inRange(hsv_roi, np.array((0., 60.,32.)), np.array((180.,255.,255.))) 
roi_hist = cv2.calcHist([hsv_roi],[0],mask,[180],[0,180]) 
cv2.normalize(roi_hist,roi_hist,0,255,cv2.NORM_MINMAX)
# Setup the termination criteria, either 10 iteration or move by atleast 1 pt
term_crit = ( cv2.TERM_CRITERIA_EPS | cv2.TERM_CRITERIA_COUNT, 10, 1 )

while(1):
    ret ,frame = cap.read()
    if ret == True:
        hsv = cv2.cvtColor(frame, cv2.COLOR_BGR2HSV)
        dst = cv2.calcBackProject([hsv],[0],roi_hist,[0,180],1)
        # apply meanshift to get the new location
        ret, track_window = cv2.meanShift(dst, track_window, term_crit)
        # Draw it on image
        x,y,w,h = track_window
        img2 = cv2.rectangle(frame, (x,y), (x+w,y+h), 255,2) 
        cv2.imshow('img2',img2)
        k = cv2.waitKey(60) & 0xff
        if k == 27:
            break 
        else:
            cv2.imwrite(chr(k)+".jpg",img2)
    else:
        break

cv2.destroyAllWindows() cap.release()

下面是使用  meanshift   算法对一个视频前三帧分析的结果：

 

39.2 Camshift

上面的结果有一个问题。我们的窗口的大小是固定的,而汽车由远及近（在视觉上）是一个逐渐变大的过程,固定的窗口是不合适的。所以我们需要根据目标的大小和角度来对窗口的大小和角度进行修订。OpenCVLabs 为我们带来的解决方案（这个解决方案来自“OpenCV实验室”，它被称为CAMshift(连续自适应Meanshift)，由Gary Bradsky于1998年在它的论文“用于感知用户界面的计算机视觉人脸跟踪”中发表）。这个算法首先要使用 meanshift,meanshift 找到（并覆盖）目标之后, 再去调整窗口的大小, 。它还会计算目标对象的最佳外接椭圆的角度,并以此调节窗口角度。然后使用更新后的窗口大小和角度来在原来的位 置继续进行 meanshift。重复这个过程知道达到需要的精度。如下图所示:

与 Meanshift 基本一样,但是返回的结果是一个带旋转角度的矩形（这是 我们的结果）,以及这个矩形的参数（被用到下一次迭代过程中）。下面是代码：

import numpy as np 
import cv2

cap = cv2.VideoCapture('slow.flv')
# take first frame of the video
ret,frame = cap.read()
# setup initial location of window
r,h,c,w = 250,90,400,125  # simply hardcoded the values
track_window = (c,r,w,h)
# set up the ROI for tracking
roi = frame[r:r+h, c:c+w]
hsv_roi =  cv2.cvtColor(frame, cv2.COLOR_BGR2HSV)
mask = cv2.inRange(hsv_roi, np.array((0., 60.,32.)), np.array((180.,255.,255.))) 
roi_hist = cv2.calcHist([hsv_roi],[0],mask,[180],[0,180]) 
cv2.normalize(roi_hist,roi_hist,0,255,cv2.NORM_MINMAX)
# Setup the termination criteria, either 10 iteration or move by atleast 1 pt
term_crit = ( cv2.TERM_CRITERIA_EPS | cv2.TERM_CRITERIA_COUNT, 10, 1 )
while(1):
    ret ,frame = cap.read()
    if ret == True:
        hsv = cv2.cvtColor(frame, cv2.COLOR_BGR2HSV)
        dst = cv2.calcBackProject([hsv],[0],roi_hist,[0,180],1)
        # apply meanshift to get the new location
        ret, track_window = cv2.CamShift(dst, track_window, term_crit)
        # Draw it on image
        pts = cv2.boxPoints(ret) 
        pts = np.int0(pts)
        img2 = cv2.polylines(frame,[pts],True, 255,2) 
        cv2.imshow('img2',img2)
        k = cv2.waitKey(60) & 0xff
        if k == 27:
            break 
        else:
            cv2.imwrite(chr(k)+".jpg",img2)
    else:
        break

cv2.destroyAllWindows() 
cap.release()

对三帧图像分析的结果如下：

OpenCV 的官方示例中有一个 camshift 的交互式演示:

'''
Camshift tracker
================
这个demo演示了基于均值漂移(Camshift )的跟踪
你选择一个颜色对象，比如你的脸，它会跟踪它。这将从摄像机读取数据(默认为0，或用户输入的摄像机编号)

 http://www.robinhewitt.com/research/track/camshift.html
Usage:
------
camshift.py [

40.光流

由于目标对象或者摄像机的移动造成的图像对象在连续两帧图像中的移动被称为光流。它是一个 2D 向量场,可以用来显示一个点从第一帧图像到第二 帧图像之间的移动。如下图所示（Image Courtesy: Wikipedia article on Optical  Flow）：

上图显示了一个点在连续五帧图像间的移动。箭头表示光流场向量。光流在很多领域中都很有用,比如：

• 由运动重建结构

• 视频压缩

• 视频稳定... 

光流是基于以下假设的：

1.  在连续的两帧图像之间（目标对象的）像素的灰度值不改变。

2.  相邻的像素具有相同的运动

第一帧图像中的像素 I (x,y,t) 在时间 dt 后移动到第二帧图像的（x+dx,y+dy）处。根据第一条假设：灰度值不变。所以我们可以得到：

I (x, y, t) = I (x + dx, y + dy, t + dt)

对等号右侧进行泰勒级数展开,消去相同项,两边都除以 dt,得到如下方程：

fxu + fyv + ft = 0

其中：

上边的等式叫做光流方程。其中 fx 和 fy 是图像梯度,同样 ft 是时间方向 的梯度。但（u,v）是不知道的。我们不能在一个等式中求解两个未知数。有 几个方法可以帮我们解决这个问题,其中的一个是 Lucas-Kanade 法

40.1 OpenCV中的Lucas-Kanade 光流

现在我们要使用第二条假设,邻域内的所有点都有相似的运动。Lucas- Kanade 法就是利用一个 3x3 邻域中的 9 个点具有相同运动的这一点。这样 我们就可以找到这 9 个点的光流方程,用它们组成一个具有两个未知数 9 个等 式的方程组,这是一个约束条件过多的方程组。一个好的解决方法就是使用最 小二乘拟合。下面就是求解结果：

（有没有发现上边的逆矩阵与 Harris 角点检测器非常相似,这说明角点很适合被用来做跟踪）

从使用者的角度来看,想法很简单,我们取跟踪一些点,然后我们就会获得 这些点的光流向量。但是还有一些问题。直到现在我们处理的都是很小的运动。 如果有大的运动怎么办呢？图像金字塔。我们可以使用图像金字塔的顶层,此 时小的运动被移除,大的运动装换成了小的运动,现在再使用 Lucas-Kanade 算法,我们就会得到尺度空间上的光流。

上述所有过程都被 OpenCV 打包成了一个函数：cv2.calcOpticalFlowPyrLK()。 现在我们使用这个函数创建一个小程序来跟踪视频中的一些点。要跟踪那些点 呢？我们使用函数 cv2.goodFeatureToTrack() 来确定要跟踪的点。首先在视频的第一帧图像中检测一些 Shi-Tomasi 角点,然后我们使用 Lucas-Kanade 算法迭代跟踪这些角点。我们要给函数 cv2.calcOpticlaFlowPyrLK()传入前一帧图像和其中的点,以及下一帧图像。函数将返回带有状态数的点, 如果状态数是 1,那说明在下一帧图像中找到了这个点（上一帧中角点）,如果 状态数是 0,就说明没有在下一帧图像中找到这个点。我们再把这些点作为参 数传给函数,如此迭代下去实现跟踪。代码如下：

import numpy as np
import cv2

cap = cv2.VideoCapture('slow.flv')
# params for ShiTomasi corner detection
feature_params = dict(maxCorners=100, qualityLevel=0.3, minDistance=7, blockSize=7)

# Parameters for lucas kanade optical flow
# maxLevel 为使用的图像金字塔层数
lk_params = dict(winSize=(15, 15), maxLevel=2,
                 criteria=(cv2.TERM_CRITERIA_EPS | cv2.TERM_CRITERIA_COUNT, 10, 0.03))

# Create some random colors
color = np.random.randint(0, 255, (100, 3))
# Take first frame and find corners in it
ret, old_frame = cap.read()
old_gray = cv2.cvtColor(old_frame, cv2.COLOR_BGR2GRAY)
p0 = cv2.goodFeaturesToTrack(old_gray, mask=None, **feature_params)
# Create a mask image for drawing purposes
mask = np.zeros_like(old_frame)

while (1):
    ret, frame = cap.read()
    frame_gray = cv2.cvtColor(frame, cv2.COLOR_BGR2GRAY)
    # calculate optical flow 能够获取点的新位置
    p1, st, err = cv2.calcOpticalFlowPyrLK(old_gray, frame_gray, p0, None, **lk_params)
    # Select good points
    good_new = p1[st == 1]
    good_old = p0[st == 1]
    # draw the tracks
    for i, (new, old) in enumerate(zip(good_new, good_old)):
        a, b = new.ravel()
        c, d = old.ravel()
        mask = cv2.line(mask, (a, b), (c, d), color[i].tolist(), 2)
        frame = cv2.circle(frame, (a, b), 5, color[i].tolist(), -1)
    img = cv2.add(frame, mask)

    cv2.imshow('frame', img)
    k = cv2.waitKey(30) & 0xff
    if k == 27:
        break
    
    # Now update the previous frame and previous points
    old_gray = frame_gray.copy()
    p0 = good_new.reshape(-1, 1, 2)

cv2.destroyAllWindows()
cap.release()

下面是结果：

(上面的代码没有对返回角点的正确性进行检查。图像中的一些特征点甚至 在丢失以后,光流还会找到一个预期相似的点。所以为了实现稳定的跟踪,我们应该每个一定间隔就要进行一次角点检测。OpenCV 的官方示例中带有这样 一个例子,它是每 5 帧进行一个特征点检测。它还对光流点使用反向检测来选取好的点进行跟踪。示例为/samples/python2/lk_track.py)

40.2 OpenCV中的稠密光流

Lucas-Kanade方法计算稀疏特征集的光流(在我们的示例中，使用Shi-Tomasi算法检测拐角)。OpenCV提供了另一种寻找稠密光流的算法。它计算帧中所有点的光流。它基于Gunner Farneback的算法，Gunner Farneback在2003年的“基于多项式展开的两帧运动估计”中解释了该算法。

下面的例子使用上面的算法计算稠密光流。结果是一个带有光流向量（u,v）的双通道数组。通过计算我们能得到光流的大小和方向。我们使用颜色对结果进行编码以便于更好的观察。方向对应于 H（Hue）通道,大小对应 于V（Value）通道。代码如下：

import cv2
import numpy as np

cap = cv2.VideoCapture("vtest.avi")

ret, frame1 = cap.read()
prvs = cv2.cvtColor(frame1, cv2.COLOR_BGR2GRAY)
hsv = np.zeros_like(frame1)
hsv[..., 1] = 255

while (1):
    ret, frame2 = cap.read()
    next = cv2.cvtColor(frame2, cv2.COLOR_BGR2GRAY)
    # cv2.calcOpticalFlowFarneback(prev, next, pyr_scale, levels, winsize, iterations, poly_n, poly_sigma, flags[)
    # pyr_scale – parameter, specifying the image scale (<1) to build pyramids for each image; pyr_scale=0.5 means a classical pyramid, where each next layer is twice smaller than the previous one.
    # poly_n – size of the pixel neighborhood used to find polynomial expansion in each pixel; typically poly_n =5 or 7.
    # poly_sigma – standard deviation of the Gaussian that is used to smooth derivatives used as a basis for the polynomial expansion; for poly_n=5, you can set poly_sigma=1.1, for poly_n=7, a good value would be poly_sigma=1.5.
    # flag(可选) - 0或1,0计算快,1慢但准确
    flow = cv2.calcOpticalFlowFarneback(prvs, next, None, 0.5, 3, 15, 3, 5, 1.2, 0)
    
    # cv2.cartToPolar Calculates the magnitude and angle of 2D vectors.
    mag, ang = cv2.cartToPolar(flow[..., 0], flow[..., 1])
    hsv[..., 0] = ang * 180 / np.pi / 2
    hsv[..., 2] = cv2.normalize(mag, None, 0, 255, cv2.NORM_MINMAX)
    rgb = cv2.cvtColor(hsv, cv2.COLOR_HSV2BGR)

    cv2.imshow('frame2', rgb)
    k = cv2.waitKey(30) & 0xff
    if k == 27:
        break
    elif k == ord('s'):
        cv2.imwrite('opticalfb.png', frame2)
        cv2.imwrite('opticalhsv.png', rgb)
    prvs = next

cap.release()
cv2.destroyAllWindows()

结果如下：

OpenCV 官方示例中有一个更高级的稠密光流/samples/python2/opt_flow.py！

41.背景减除

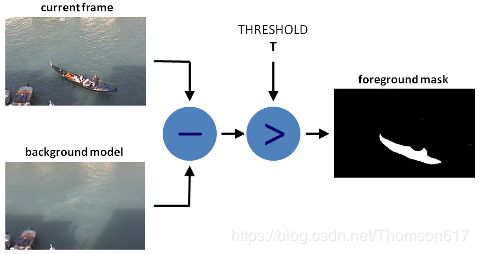
背景减除(Background subtraction,BS)是一种使用静态相机生成前景掩码(即包含场景中移动物体像素的二值图像)的常用技术。顾名思义，BS计算前景掩码，执行当前帧和背景模型之间的减法，包含场景的静态部分，或者更一般地说，考虑到所观察场景的特征，所有可以被视为背景的部分。

后台建模包括两个主要步骤：

1.后台初始化；

2.后台更新。

第一步，计算背景的初始模型，而在第二步中，更新模型以适应场景中可能的变化。

在很多基础应用中背景减除都是一个非常重要的步骤。例如顾客统计中使用一个静态摄像头来记录进入和离开房间的人数,或者是交通摄像头中需要提取交通工具的信息等。在所有的这些例子中,首先要将人或车单独提取出来。 技术上来说,我们需要从静止的背景中提取移动的前景。

如果你有一张背景（仅有背景不含前景）图像,比如没有顾客的房间,没有交通工具的道路等,那就好办了。我们只需要在新图像中减去背景就可以得到前景对象了。但是在大多数情况下,我们没有这样的（背景）图像,所以我们需要从现有图像中提取背景。如果图像中的交通工具有影子时这个工作就更难了,因为影子也在移动,仅仅使用减法会把影子也当成前景。 真是一件很复杂的事情。为了实现这个目的,科学家们已经提出了几种算法。OpenCV 中已经包含了很多比较容易使用的方法。如下所示:

cv::Algorithm	cv::BackgroundSubtractor	cv::BackgroundSubtractorKNN
		cv::BackgroundSubtractorMOG2
		cv::bgsegm::BackgroundSubtractorCNT
		cv::bgsegm::BackgroundSubtractorGMG
		cv::bgsegm::BackgroundSubtractorGSOC
		cv::bgsegm::BackgroundSubtractorLSBP
		cv::bgsegm::BackgroundSubtractorMOG
		cv::cuda::BackgroundSubtractorFGD
		cv::cuda::BackgroundSubtractorGMG
		cv::cuda::BackgroundSubtractorMOG

(1).BackgroundSubtractorMOG

这是一个以混合高斯模型为基础的前景/背景分割算法。它是   P.KadewTraKuPong 和 R.Bowden 在 2001 年提出的。它使用 K（K=3 或 5）个高斯分布混合对 背景像素进行建模。使用这些颜色（在整个视频中）存在时间的长短作为混合 的权重。背景的颜色一般持续的时间最长,而且更加静止。一个像素怎么会有 分布呢？在 x,y 平面上一个像素就是一个像素没有分布,但是我们现在讲的 背景建模是基于时间序列的,因此每一个像素点所在的位置在整个时间序列中 就会有很多值,从而构成一个分布。

在编写代码时,我们需要使用函数：cv2.createBackgroundSubtractorMOG() 创建一个背景对象。这个函数有些可选参数,比如要进行建模场景的时间长度, 高斯混合成分的数量,阈值等。将它们全部设置为默认值。然后在整个视频中 我们是需要使用   backgroundsubtractor.apply() 就可以得到前景的掩模了。

下面是一个简单的例子：

import cv2

cap = cv2.VideoCapture(0)
fgbg = cv2.createBackgroundSubtractorMOG()
while(1):
    ret, frame = cap.read()
    fgmask = fgbg.apply(frame)
    cv2.imshow('frame',fgmask) 
    k = cv2.waitKey(30) & 0xff 
    if k == 27:
        break
cap.release() 
cv2.destroyAllWindows()

原始图像

下图显示了一段视频中的第  200 帧图像

MOG的结果:

(2).BackgroundSubtractorMOG2

这个也是以高斯混合模型为基础的背景/前景分割算法。它是以 2004 年 和 2006 年 Z.Zivkovic 的两篇文章为基础的。这个算法的一个特点是它为每 一个像素选择一个合适数目的高斯分布。（上一个方法中我们使用是 K 高斯分 布）。这样就会对由于亮度等发生变化引起的场景变化产生更好的适应。

和前面一样我们需要创建一个背景对象。但在这里我们我们可以选择是否 检测阴影。如果 detectShadows = True（默认值）,它就会检测并将影子标记出来,但是这样做会降低处理速度。影子会被标记为灰色。

import cv2

cap = cv2.VideoCapture('vtest.avi')
fgbg = cv2.createBackgroundSubtractorMOG2()
while(1):
    ret, frame = cap.read()
    fgmask = fgbg.apply(frame)
    cv2.imshow('frame',fgmask) 
    k = cv2.waitKey(30) & 0xff 
    if k == 27:
        break
cap.release() 
cv2.destroyAllWindows()

MOG2的结果(灰色区域代表阴影):

(3).BackgroundSubtractorGMG

此算法结合了静态背景图像估计和每个像素的贝叶斯分割。这是 2012 年 Andrew_B.Godbehere,Akihiro_Matsukawa 和 Ken_Goldberg 在文章中提出的。

它使用前面很少的图像（默认为前 120 帧）进行背景建模。使用了概率前景估计算法（使用贝叶斯估计鉴定前景）。这是一种自适应的估计,新观察到的对象比旧的对象具有更高的权重,从而对光照变化产生适应。一些形态学操作如开运算闭运算等被用来除去不需要的噪音。在前几帧图像中你会得到一个黑色窗口。

对结果进行形态学开运算对与去除噪声很有帮助。

import cv2

cap = cv2.VideoCapture('vtest.avi')
kernel = cv2.getStructuringElement(cv2.MORPH_ELLIPSE,(3,3)) 
fgbg = cv2.createBackgroundSubtractorGMG()
while(1):
    ret, frame = cap.read()
    fgmask = fgbg.apply(frame)
    fgmask = cv2.morphologyEx(fgmask, cv2.MORPH_OPEN, kernel)
    cv2.imshow('frame',fgmask) 
    k = cv2.waitKey(30) & 0xff 
    if k == 27:
        break
cap.release() 
cv2.destroyAllWindows()

GMG 的结果(使用形态学开运算将噪音去除):

(4).BackgroundSubtractorKNN

基于k近邻的背景/前景分割算法。该类实现了[248]中描述的k近邻背景减法。如果前景像素的数量比较低将非常有效。示例如下:

backgroundSubtractor = cv2.createBackgroundSubtractorKNN(detectShadows=True)
structuringElement = cv2.getStructuringElement(cv2.MORPH_ELLIPSE, (3, 3))

# 利用帧差法获取矩形框
def getBoxes(frame, backgroundSubtractor, structuringElement):
    boxes = []
    gray_L = cv2.cvtColor(frame, cv2.COLOR_BGR2GRAY)
    fgmask = backgroundSubtractor.apply(gray_L)  # 背景分割器，该函数计算了前景掩码
    # 二值化阈值处理，前景掩码含有前景的白色值以及阴影的灰色值，在阈值化图像中，将非纯白色（244~255）的所有像素都设为0，而不是255
    th = cv2.threshold(fgmask.copy(), 244, 255, cv2.THRESH_BINARY)[1]
    dilated = cv2.dilate(th, structuringElement, iterations=2)  # 形态学膨胀
    # 该函数计算一幅图像中目标的轮廓
    contours, hierarchy = cv2.findContours(image=dilated, mode=cv2.RETR_EXTERNAL,method=cv2.CHAIN_APPROX_SIMPLE)
    for cnt in contours:
        if cv2.contourArea(cnt) > 2000:
            (x, y, w, h) = cv2.boundingRect(cnt)  # 外接矩形
            boxes.append((x, y, w, h))

    return frame, boxes

KNN的结果(灰色区域为检测到的阴影):

因篇幅过长,后续部分参见:OpenCV-Python (官方)中文教程(部分三)