一种高效的Polar码冻结比特编译码方法

注：此为论文读书笔记
英文论文原名为：《Efficient Method for Frozen Bits Encoding and Decoding of PolarCode》

Abstract： 本研究提出了一种利用代数方法对Polar码进行高效编码和解码以发现错误模式的方法。所提出的解码方法背后的关键思想是理论上基于冻结比特和可纠正错误模式之间存在一对一映射。当解码(N=8，K=4)和(N=16，K=8)极性码时，该方法将有助于减少寻找错误模式的解码时间。此外，使用G3和G4矩阵的查找表可以将编码减少91％，并且该编码方法可以用于代数方法对Polar Code的解码。(it would reduce the encoding by 91% with lookup table for G3 and G4 matrix and the encoding method can be used to the decoding of Polar Code with algebraic method. )最终，所提出的Polar码解码算法可以变得规则，简单并适合于软件实现。

1 Introduction

Polar码的编码是Arıkan[1]最近证实的一种线性分组编码方法，它不仅能纠正错误，而且逼近Shannon-Hartley定理，这引起了研究者的兴趣，该码体系结构的解码并不复杂， 数据在纠错性能方面的可靠性极好。由于编码和译码的复杂性，它随着码长的增加呈对数增长。如果使用逐次抵消( Successive Cancelation，SC)算法[2-4]，则译码复杂度几乎没有增加。然而，SC译码算法在较长的译码过程中，其纠错性能不如Turbo码和LDPC码，近年来的研究文献中针对SC译码算法的方法改进[5-9]。例如，诸如列表SC（s List SC，SCL），堆栈SC（Stack SC，SSC），循环冗余校验器辅助的SCL（Cyclic Redundancy Checker-assisted SCL，CRC-SCL）等算法的性能。这些方法也被实现为硬件电路[10]，并且这些译码技术文档仅侧重于软判决模式来讨论纠错性能。由于极化码的标准形式是非系统码[1]，并且在[11]中提到系统码具有比非系统码更低的误比特率(BER)。因此，本文的编码方法采用查表法和代数算法相结合的方法进行纠错，极化码的纠错算法将利用冻结比特所呈现的特性。由于无差错解码后冻结比特必须为零，利用这一特性，解决实际通信中可能出现的数据差错，可以建立一个简单的纠错规则。

2 实验方法

将分为三个部分进行说明：生成矩阵Generation Matrix，编码encoding，解码decoding 和纠错error correction。

2.1 Generation Matrix

生成矩阵的定义如下：
$$G=\left[\begin{array}{cc}1& 1\\ 0& 1\end{array}\right]\text{\hspace{1em}(1)}$$
生成矩阵的扩展矩阵的定义如下，使用Kronecker乘积生成编码和解码矩阵：

在本文中，它将使用


由于Polar码结构的生成矩阵与Reed-Muller（RM）码的生成有关，因此生成器矩阵具有上三角的特征，这也意味着编码矩阵是逆矩阵

Encoding

8位原始数据的向量如下：
$$D=(d_0,d_1,d_2,d_3,d_4,d_5,d_6,d_7)$$
8位冻结位的向量，其元素必须为零，如下所示：
$$F=(f_0,f_1,f_2,f_3,f_4,f_5,f_6,f_7)$$
具有16位数据的向量D和F如下所示：
$$\begin{gathered} M=(f_0,f_1,f_2,d_0,f_3,f_4,d_1,f_5,f_6,d_2,d_3,d_4,f_7,d_5,d_6,d_7) \\ =(m_0,m_1,m_2,m_3,m_4,m_5,m_6,m_7,m_8,m_9,m_{10},m_{11},m_{12},m_{13},m_{14},m_{15}) \end{gathered}$$

原始方法

原始的编码和解码方法是使用矩阵运算来获得结果。 具体操作如下：

这将需要256次AND运算和240次XOR运算。$G^4$的下三角部分不需要计算，因此实际上只需要136个AND运算和120个XOR运算。

查找表方法

在讨论有关Polar码编码和解码的查找表方法之前，需要先通过矩阵乘法$G^3$和$X_j=(x_0,x_1,x_2,x_3,x_4,x_5,x_6,x_7)$建立表$T$,$X_j$是0到255的二进制组合,$X^{\prime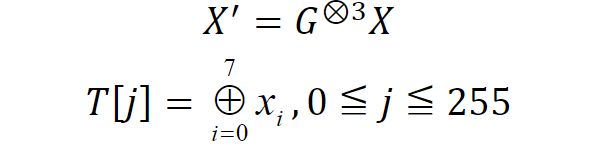 }$是结果：

在这里的$T[j]$这个公式与j没关系啊？？？？？

把$M$分离成$M_0$和$M_1$两部分：


并形成两个新的8 * 8矩阵$P_0,P_1$,整两个矩阵取自$G^4$的一部分。实际上，这是Kronecker产生的结果

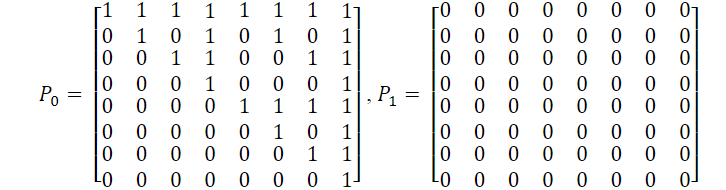
原始的Polar码区域的编码和解码公式如下

以上$M^{\prime }$矩阵可以分为四个子矩阵，如下所示：

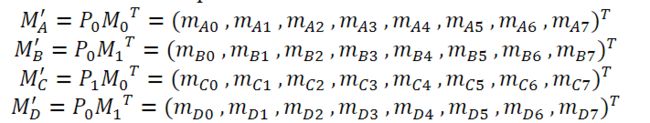
$P_{0d}，P_{1d}$的每一行都可以分别用(255,85,51,17,15,5,3,1)和(0,0,0,0,0,0,0,0)表示数组$P_{0d}[],P_{1d}[]$
$M_0,M_1$以十进制表示$m_{0-7},m_{8-15}$。然后使用前面提到的表和查找表，$m_{C0-7}$结果必须为0，$m_{D0-7}=m_{B0-7}$，因此，这两个部分都不需要计算：

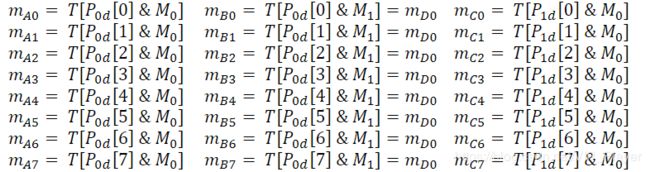
后续操作按如下方式完成：

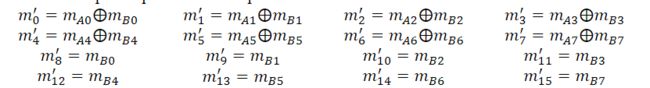
查找表法将需要16次AND运算和8次XOR运算。

另外还有16倍的查询表。

只写了编码 我只需要看编码就可以了