基于SVM的划线框识别（1）HOG特征提取

虽然上过机器学习的课程，但是那么课既没有课程设计也没有需要敲代码的作业，寻思着毕业设计选一个来挑战一下。“划线框识别”这个题目有两个，一个是深度学习实现，另一个是支持向量机实现，和舍友一人选了一个。考研复试结束了没什么事情，开始动手写这个，指不定自己哪天就忘了。

还是写博客舒服，写论文太痛苦。

工具

python  +  libsvm  +  opencv

SVM选择的是C_SVC和RBF内核

背景

刚刚看到题目的时候我以为“划线框”和高中时候用的答题卡差不多，后来给了数据集，感觉没人会叫这东西划线框吧...看了一下确实没有见过，可能一些调查问卷会用这种？调查问卷也只接触过打 √ 打勾的，倒是不需要用2B铅笔来涂。

目标就是用这些数据训练一个SVM模型来实现对这种划线框的识别。

划线框的图片示例（一部分）：

有效样本

无效样本

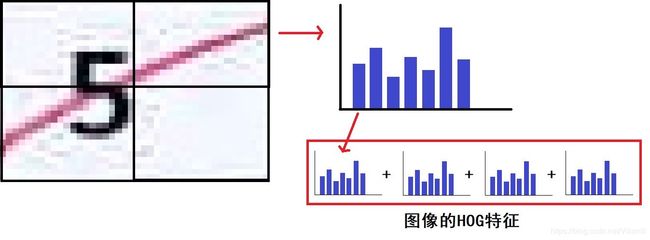
HOG特征提取

选择的特征是HOG特征，后期的时候准确率上不去，想到既然样本里笔迹都是红色的，那么是不是也可以用一下颜色，加了颜色直方图特征，结果相比于原来只用HOG，效果并没有什么变化。

学习的时候参考的是：

python opencv教程里面使用SVM进行手写图片识别以及Histogram of Oriented Gradients，其实搜一下HOG能发现很多博客都翻译过这篇文章。比较着这两篇里面的讲述和代码，差不多能够理解HOG特征提取的流程。在按照这两篇文章学习时的一些问题：

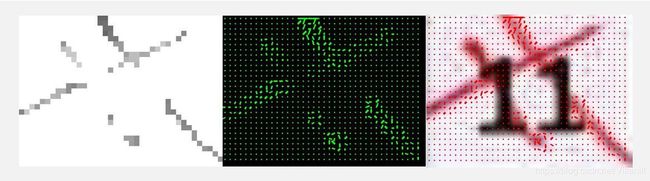
1、我通过Sobel算子在水平方向和竖直方向卷积之后得到的图像如下。

1：原图像，2：Gx，3：Gy，4：梯度图像

而Histogram of Oriented Gradients中使用算子卷积之后的图像是像下面这样的。（分别对应上图的2-4）

出现这样的情况是因为我计算完梯度之后再显示图片时，每个像素点处值的范围是0~255，只需将其映射到0~1即可。

img = np.float32(img)/255.0

越亮的地方值越大，说明梯度变化也越大。

2、因为最后的block是为了归一化，来减小光照的影响，我看了一下手里的样本，光照的影响几乎没有，于是就将最后block那一步给省略掉了。

HOG特征提取实现代码

计算HOG特征的代码放在末尾，拆开说说其中的几个部分。

1、提取特征之前的预处理。一开始我只是单纯地使用一个阈值进行划分，将图像转换为二值图像，但是在后期训练的时候我发现这样的处理有问题。像是下面这个图像，仅使用单个阈值进行二值化，选项“11”本身在二值化后是被保留的。

但我们其实并不关心黑色选项，我们只关心红色的笔迹。而且因为有的选项是个位数，有的选项是两位数，有的甚至带着小数点，就会导致选项对提取出的特征有很大的影响，所以需要排除选项对特征提取的干扰。

后期正确率一直上不去。我一开始以为是特征维度不够，试着将HOG划分的更细，也试着增加了颜色直方图特征。对准确率的提升效果都不大。后来使用了双阈值划分，即设置两个阈值min和max，如果像素点的值在min和max之间，那么值被保留，否则被置为0。

1.原图像   2.双阈值划分后  3.腐蚀后  4.按位取反后

腐蚀是因为只靠双阈值划分还是会有选项的一些边缘残留，因为我的样本图像本身尺寸就很小，只能使用最小的2x2大小的腐蚀算子，用3x3的就差不多已经渣都不剩了。

#输入图像路径，将图像通过两个阈值分割
#阈值分割后的图像按2*2的邻域大小的模板进行腐蚀，只留下划线框
def HandleImgByThreshAndErode(img_gray):
    #读取灰度图像
    #img_gray = cv.imread(path, cv.IMREAD_GRAYSCALE)

    #两个阈值处理
    # THRESH_TOZERO将小于阈值的灰度值设为0，大于阈值的值保持不变
    retvl, img_gray = cv.threshold(img_gray, svm_parameter.bottom_thresh, 255, cv.THRESH_TOZERO)
    # THRESH_TOZERO_INV 将大于阈值的灰度值设为0，小于阈值的值保持不变
    retvl, img_gray = cv.threshold(img_gray, svm_parameter.top_thresh, 255, cv.THRESH_TOZERO_INV)

    #生成2*2的核 再大会腐蚀过头
    kernel = np.ones((2, 2), np.uint8)
    #腐蚀灰度图像 迭代一次就够了
    img_final = cv.erode(img_gray, kernel, iterations=1)
    #按位取反
    img_final = cv.bitwise_not(img_final)
    #得到的结果还是一个灰度图，可以拿去计算HOG特征

    return img_final

有了gx和gy之后就可以计算梯度向量，举一个简单情况方便理解。

    gx = cv.Sobel(img, cv.CV_32F, 1, 0)
    gy = cv.Sobel(img, cv.CV_32F, 0, 1)
    #计算梯度和梯度变化方向
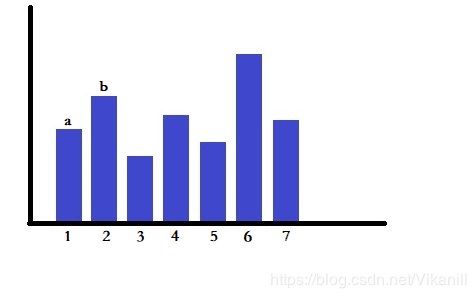
    mag, ang = cv.cartToPolar(gx, gy)

在直方图相关的概念中，bin经常出现，其实bin指的就是直方图中出现的“柱”。比如下图中就有7个bin，“bin=1”可以理解为“柱1”，其存储的值为a。

output = np.bincount(a)，a是1维数组，其元素为非负整数。计数数组a中每个元素出现的次数，然后以元素为下标，值为出现次数输出结果。

a = [1,0,0,0,5,3,0,0,1]，其中0出现了5次，1出现了2次，3和5都出现了1次,2和4出现了0次。m出现了n次，output [m]=n。

output = [5,2,0,1,0,1]

output = np.bincount(a,weight),当有第二个参数[数组]时，计算的就不再是每个元素出现的次数，而是以b中的元素作为a中对应下标元素的权重，计算a中同一元素的权重之和。

a = [1,0,0,0,5,3,0,0,1]

w = [5,1,3,4,2,1,2,2,3]

a中元素1出现在下标0的位置，那么output[1]+=w[0]，1还出现在下标8，output[1]+=w[8]。

output = [12,8,0,1,0,2]

也就是说当只有一个参数时，权重默认都是1。

关于bincount这个函数，这个老哥讲得比较清楚，当然最好还是自己动手试一试。

在python-opencv教程的代码中比较难理解的是这一行。

hists = [np.bincount(b.ravel(), m.ravel(), bin_n)  for b, m in zip(bin_cells, mag_cells)]

zip函数将bin_cells和mag_cells中的元素一对一对地打包成元组，例如a=[元素a1,元素a2,元素a3]，b=[元素b1,元素b2,元素b3]，那么zip(a,b)=[(元素a1,元素b1),(元素a2,元素b2),(元素a3,元素b3)]。然后使用for循环提取出其中的每一对，用b,m存储，以便在bincount函数中使用。

bin_cells = bins[:center_row,:center_col], 
            bins[center_row:,:center_col], 
            bins[:center_row,center_col:], 
            bins[center_row:,center_col:]
mag_cells = mag[:center_row,:center_col], 
            mag[center_row:,:center_col], 
            mag[:center_row,center_col:], 
            mag[center_row:,center_col:]

可以在上面看到，bin_cells和mag_cells都只有4个元素且都是矩阵。那么for循环中的每一对b,m也是一对矩阵。

使用ravel函数是将二维的b和m扁平化，方便进行遍历，原本n*m的数据变成(n*m)的一维数据。bins中记录的是梯度变化的方向，mag中记录的是梯度值。以方向作为bin，以梯度值为权重，计算bincount。

最终hists是一个包含4个元素的数组，这4个元素都是1维数组，每个都至少有16项。因为是都是一维数组，使用hstack相当于将他们拼接成一个数组。

hist = np.hstack(hists)

之所以要使用hstack而不是vstack，因为这4个cell每个都作为独立的一部分，使用vstack就相当于将整个图像作为一个cell，前面做的划分等工作也就没意义了。就好比你将语数英综合4门成绩列出来能看出来一个学生擅长什么不擅长什么，而只列出一个总分就只能看到他的总体水平。划分为4个cell是因为样本图像本身大小并不大。划分太小像素点都有些不够用...具体使用多少cell要根据自己的实际情况来决定。

完整代码：

def GetHOGFeature(img_src,show_img=False,show_gradient_img=False,show_gradient_img_isGray=False):
    #彩色图像，之后可能会用来显示与原图像的对比
    #img_3c = img_src.copy()
    #灰度图像
    img_1c = cv.cvtColor(img_3c,cv.COLOR_BGR2GRAY)
    #这里是自己写的一个“双阈值化+腐蚀”的函数，主要是对图像进行预处理
    img_1c = HandleImgByThreshAndErode(img_1c)

    img = img_1c.copy()
    #GetBinary是获得一个二值化函数
    img = GetBinaryImg(img)

    #bin_n为梯度直方图至少有多少列
    bin_n = 16
    #分别在水平和竖直方向使用Sobel进行卷积
    gx = cv.Sobel(img, cv.CV_32F, 1, 0)
    gy = cv.Sobel(img, cv.CV_32F, 0, 1)
    #计算梯度和梯度变化方向
    mag, ang = cv.cartToPolar(gx, gy)
    #ang为Mat类型
    #量化
    #cartToPolar默认输出的ang是弧度0到2π
    #有符号梯度 将角度的值从[0,2π]映射到[0,16]
    #bins = np.int32(bin_n*ang/(2*np.pi))
    #无符号梯度，将角度的值从[0,2π]映射到[0,16]，但是将a和a+pi看做是一样的
    bins = np.int32(bin_n*(ang%np.pi)/(np.pi))
    # 每个bins中对应的坐标x都从0到np.size(bins,1)  y从0到np.size(bins,0)

    # bins(mag)、ang图像划分为4个子矩形
    # bin_cells和mag_cell的类型应为Mat数组
    center_row = int(img.shape[0]/2)
    center_col = int(img.shape[1]/2)
    
    bin_cells = bins[:center_row,:center_col], bins[center_row:,:center_col], bins[:center_row,center_col:], bins[center_row:,center_col:]
    mag_cells = mag[:center_row,:center_col], mag[center_row:,:center_col], mag[:center_row,center_col:], mag[center_row:,center_col:]
    hists = [np.bincount(b.ravel(), m.ravel(), bin_n)  for b, m in zip(bin_cells, mag_cells)]

    hist = np.hstack(hists)
    #print("HOG特征元素个数")
    #print(len(hist))

    #保留2位小数方便计算
    hist = np.round(hist,2)

    return hist

可视化

试着根据计算出来的梯度向量在原图像上绘制了一下。能让效果直观一点。