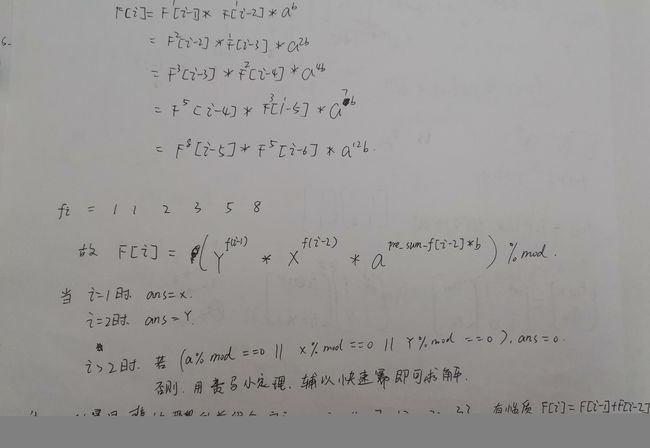2020牛客寒假算法基础集训营1 题解

知识点： 字符串，贪心，矩阵快速幂，概率论，计算几何，并查集，数论

A题 honoka和格点三角形

纸上画一画，即可推出公式。
计算会出现重复，箭头即为存在冲突，这里m-2就是去重，最后乘2，因为四种情况，是两两对称的。

#include 
using namespace std;
typedef long long ll;
const ll mod = 1e9 + 7;
int main()
{
    ll n, m;
    scanf("%lld %lld", &n, &m);
    ll ans = 2 * (n + m - 2) % mod *( (n - 1) * (m - 2) % mod + (n - 2) * (m - 1) % mod) % mod;
    printf("%lld\n", ans);
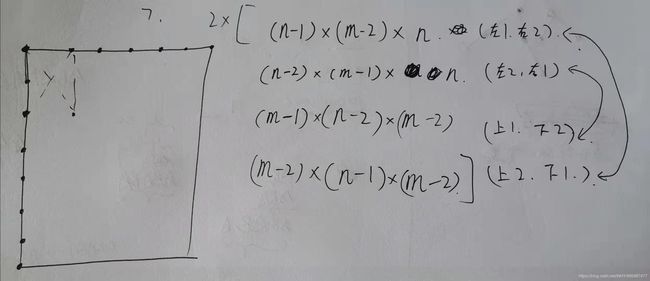
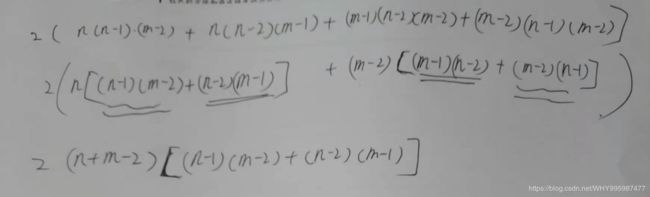
    return 0;
}

B题 kotori和bangdream

水题

#include 
using namespace std;
typedef long long ll;
const int maxn = 1e5 + 5;
int main()
{
    int n, x, a, b;
    scanf("%d %d %d %d", &n, &x, &a, &b);
    double ans = 0.01 * x * a * n + 0.01 * (100 - x) * b * n;
    printf("%.2f\n", ans);   
    return 0;
}

C题 umi和弓道

计算几何，题目要求能射中的点小于等于k个，那么我把k的值更新为k = n - k，那么目标就转化为在某个坐标轴上用最短挡板挡住k个点。
分别存储人与靶在x轴和y轴上的交点，然后分别在x轴和y轴上尺取k个交点，取最短距离即为答案。

#include 
using namespace std;
typedef long long ll;
const int maxn = 1e5 + 5;
const int INF = 0x3f3f3f3f;
const ll mod = 1e9 + 7;

vector <double> v1, v2;//分别为x0 y0 与点在 x轴和y轴上的交点

int main()
{
    double x0, y0;
    int n, k;
    cin >> x0 >> y0 >> n >> k;
    k = n - k;
    //目标转换为遮挡住k个点
    for(int i = 1; i <= n; i++)
    {
        double x, y;
        cin >> x >> y;
        if(x0 * x < 0)//y轴上有交点
        {
            v2.push_back(y0 - (y0 - y) * x0 / (x0 - x) );
        }
        if(y0 * y < 0)
        {
            v1.push_back(x0 - y0 * (x0 - x) / (y0 - y) );
        }
    }

    double mi = 1e18;
    sort(v1.begin(), v1.end());
    sort(v2.begin(), v2.end());

    if(v1.size() >= k)//至少有k个能被挡住
    {
        int l = 0, r = k - 1;
        while(r < v1.size())
        {
            mi = min(mi, abs(v1[r] - v1[l]) );
            l++, r++;
        }
    }
    if(v2.size() >= k)
    {
        int l = 0, r = k - 1;
        while(r < v2.size())
        {
            mi = min(mi, abs(v2[r] - v2[l]) );
            l++, r++;
        }
    }
    
    if(mi == 1e18)
        printf("-1\n");
    else
        printf("%.10f", mi);
    return 0;
}

D题 hanayo和米饭

水题

#include 
using namespace std;
typedef long long ll;
const int maxn = 1e5 + 5;
int a[maxn];
int main()
{
    int n;
    scanf("%d", &n);
    for(int i = 1; i < n; i++)
    {
        scanf("%d", &a[i]);
    }
    sort(a + 1, a + n);
    for(int i = 1; i <= n; i++)
    {
        if(a[i] != i)
            return 0 * printf("%d\n", i);
    }
    return 0;
}

E题 rin和快速迭代

按题意模拟即可，每次跑出所有的因数（跑到根号）。

#include 
using namespace std;
typedef long long ll;
const int maxn = 1e5 + 5;
int main()
{
    ll n;
    scanf("%lld", &n);
    ll ans = 0;
    ll cnt = n;
    while(cnt != 2)
    {
        ans++;
        ll tem = cnt;
        cnt = 0;
        for(ll i = 1; i * i <= tem; i++)
        {
            if(tem % i == 0)
                cnt += 2;
        }
        ll num = sqrt(tem);
        if(num * num == tem)
            cnt--;
    }
    printf("%lld\n", ans);
    return 0;
}

F题 maki和tree

思路是这样的，但是当时不会代码的实现
主要在于推出公式进行时间上的优化，t1 t2，一个是维护平方和，一个是维护和，和的平方 减去 平方和 后除以2，刚好就是乘积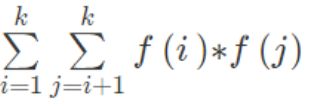

#include 
using namespace std;
typedef long long ll;
const int maxn = 1e5 + 5;
const int INF = 0x3f3f3f3f;
const ll mod = 1e9 + 7;
string color;
vector <int> g[maxn];
ll sum, ans, t1, t2;

void dfs(int p, int fa)
{
    if(color[p] == 'B')
        return ;
    sum++;//白点数量加1
    for(int i = 0; i < g[p].size(); i++)
    {
        if(g[p][i] != fa)//遍历所有没遍历过的点
            dfs(g[p][i], p);
    }
}
int main()
{
    int n;
    cin >> n >> color;
    for(int i = 1; i < n; i++)
    {
        int x, y;
        scanf("%d %d", &x, &y);
        g[x].push_back(y);
        g[y].push_back(x);
    }
    for(int i = 1; i <= n; i++)
    {
        t1 = t2 = 0;
        if(color[i] == 'B')//如果是黑色，从黑色开始搜索
        {
            for(int j = 0; j < g[i].size(); j++)//遍历与黑点连接的所有点
            {
                sum = 0;
                dfs(g[i][j], g[i][j]);//对白点进行深搜
                ans += sum;
                t1 += sum;
                t2 += sum * sum;
            }
        }
        ans += (t1 * t1 - t2) / 2;//公式化简
    }
    printf("%lld\n", ans);
    return 0;
}

G题 eli和字符串

记录每种字母的位置信息，在符合题意情况下，取位置差值的最小值。

#include 
using namespace std;
typedef long long ll;
const int maxn = 2e5 + 5;
const int INF = 0x3f3f3f3f;
char s[maxn];
vector <int> pos[257];
int main()
{
    int n, k;
    scanf("%d %d", &n, &k);
    scanf("%s", s + 1);
    for(int i = 1; i <= n; i++)
    {
        char ch = s[i];
        pos[ch].push_back(i);
    }

    int ans = INF;
    for(int i = 1; i <= 256; i++)
    {
        if(pos[i].size() >= k)
        {
            for(int j = 0; j < pos[i].size() - k + 1; j++)
                ans = min(ans, pos[i][j + k - 1] - pos[i][j] + 1);
        }
    }
    if(ans == INF)
        printf("-1\n");
    else
        printf("%d\n", ans);
    return 0;
}

H题 nozomi和字符串

要么只把0换成1，要么只把1换成0，用两个尺取获取最大距离。

#include 
using namespace std;
typedef long long ll;
const ll mod = 1e9 + 7;
const int maxn = 2e5 + 10;
char s[maxn];
int pre0[maxn];
int pre1[maxn];
int main()
{
    int n, k;
    scanf("%d %d", &n, &k);
    scanf("%s", s + 1);
    for(int i = 1; i <= n; i++)
    {
        if(s[i] == '0')
        {
            pre0[i] = pre0[i - 1] + 1;
            pre1[i] = pre1[i - 1];
        }
        else
        {
            pre1[i] = pre1[i - 1] + 1;
            pre0[i] = pre0[i - 1];
        }
    }
    //尺取0
    int L = 0, R = 1;
    int ans = 0;
    while(R <= n)
    {
        while(R <= n && pre0[R] - pre0[L] <= k)
        {
            ans = max(ans, R - L);
            R++;
        }
        L++;
    }
    //尺取1
    int L1 = 0, R1 = 1;
    int ans1 = 0;
    while(R1 <= n)
    {
        while(R1 <= n && pre1[R1] - pre1[L1] <= k)
        {
            ans1 = max(ans1, R1 - L1);
            R1++;
        }
        L1++;
    }
    printf("%d\n", max(ans, ans1));
    return 0;
}

I题 nico和niconiconi

一道dp题，其实不难。
转移方程就是那么的……朴实无华。

#include
using namespace std;
#define ll long long
ll dp[322222]={0};
string a;
int main(){
 
    ll i,n,x,y,z;
    cin>>n>>x>>y>>z;
    cin>>a;
    for(i=0;i<n;i++){
        if(i>0)dp[i]=dp[i-1];
        if(i>=3&&a[i-3]=='n'&&a[i-2]=='i'&&a[i-1]=='c'&&a[i]=='o')
            dp[i]=max(dp[i],dp[i-3]+x);
        if(i>=5&&a[i-5]=='n'&&a[i-4]=='i'&&a[i-3]=='c'&&a[i-2]=='o'&&a[i-1]=='n'&&a[i]=='i')
            dp[i]=max(dp[i],dp[i-5]+y);
        if(i>=9&&a[i-9]=='n'&&a[i-8]=='i'&&a[i-7]=='c'&&a[i-6]=='o'&&a[i-5]=='n'&&a[i-4]=='i'&&a[i-3]=='c'&&a[i-2]=='o'&&a[i-1]=='n'&&a[i]=='i')
            dp[i]=max(dp[i],dp[i-9]+z);
    }
    //这里偷懒了，对于字符a[i]='n'的情况，显然dp[i]=dp[i-1]。这样就不用处理dp[-1]的值。
    cout<<dp[n-1];
}

J题 u’s的影响力

这道题是在下面这道题的基础上修改的： http://www.z4zr.com/page/450.html

比赛结束后样例增强了，找了几个榜上ak的人的代码，他们都过不了。

赛后我调试了很久，终于过了。

#include 
using namespace std;
typedef long long ll;
const int maxn = 1e5 + 5;
const int INF = 0x3f3f3f3f;
const ll mod = 1e9 + 7;
ll n, x, y, a, b;
 
typedef vector <ll> vec;
typedef vector <vec> mat;
 
mat mul(mat &A, mat &B, ll mod)
{
    mat C(A.size(), vec(B[0].size()));
    for(int i = 0; i < A.size(); i++)
    {
        for(int k = 0; k < B.size(); k++)
        {
            for(int j = 0; j < B[0].size(); j++)
            {
                C[i][j] = (C[i][j] + A[i][k] * B[k][j]) % mod;
            }
        }
    }
    return C;
}
 
mat mat_pow(mat A, ll n, ll mod)
{
    mat B(A.size(), vec(A.size() ) );
    for(int i = 0; i < A.size(); i++){
        B[i][i] = 1;
    }
    while(n > 0)
    {
        if(n & 1)
            B = mul(B, A, mod);
        A = mul(A, A, mod);
        n >>= 1;
    }
    return B;
}
 
ll quick_pow(ll a, ll b)
{
    ll ans = 1;
    while(b)
    {
        if(b & 1)
            ans = ans * a % mod;
        a = a * a % mod;
        b >>= 1;
    }
    return ans;
}
int main()
{
    cin >> n >> x >> y >> a >> b;
 
    x %= mod;
    y %= mod;
 
    if(n == 1)
    {
        return 0 * printf("%lld\n", x);
    }
    else if(n == 2)
    {
        return 0 * printf("%lld\n", y);
    }
    else
    {
        if(a % mod == 0 || x % mod == 0 ||y % mod == 0)
            return 0 * printf("0\n");
            
        mat A(2, vec(2));
 
        A[0][0] = 1, A[0][1] = 1;
        A[1][0] = 1, A[1][1] = 0;
 
        A = mat_pow(A, n - 2, mod - 1);
 
        ll power_x = quick_pow(x, A[1][0]) % mod;
        ll power_y = quick_pow(y, A[0][0]) % mod;
 
        mat B(3, vec(3));
 
        B[0][0] = B[0][1] = B[0][2] = B[1][0] = B[2][2] = 1;
 
        B = mat_pow(B, n - 4, mod - 1);
 
        a = quick_pow(a % mod, b) % mod;
 
        ll mi = ((B[0][0] * 2 % (mod - 1) + B[0][1]) % (mod - 1) + B[0][2]) % (mod - 1);
 
        printf("%lld\n", power_x * power_y % mod * quick_pow(a % mod, mi % (mod - 1) ) % mod);
    }
    return 0;
}