【深度学习】EfficientNet系列网络结构
【深度学习】EfficientNet系列网络结构
- pytorch实现的EfficientNet
- MobileNetV2和Inverted residual block
- 深度可分离卷积
- Inverted residual block
- ReLU6激活函数
- MobileNetV2网络结构
- EfficientNet-B0的baseline网络结构
- Swish激活函数
- EfficientNet的网络scale up策略
- scale up策略
- 结语
pytorch实现的EfficientNet
https://github.com/lukemelas/EfficientNet-PyTorch
安装:
git clone https://github.com/lukemelas/EfficientNet-PyTorch
cd EfficientNet-Pytorch
sudo pip3 install -e .
MobileNetV2和Inverted residual block
深度可分离卷积
深度可分离卷积通过将乘法运算变为加法运算,使得在能够保证卷积精度的情况下,极大的降低运算成本。
深度可分离卷积的计算原理在【深度学习】用caffe+ShuffleNet-V2做回归中进行了说明。
标准的卷积层将一个 h i × w i × d i h_i ×w_i ×d_i hi×wi×di的tensor,通过size为 k × k k ×k k×k的卷积核,输出一个 h i × w i × d j h_i × w_i × d_j hi×wi×dj的tensor,需要的计算成本为: k × k × d i × h i × w i × d j k×k×d_i×h_i ×w_i × d_j k×k×di×hi×wi×dj,而同样size的输入输出,深度可分离卷积的计算成本为: k × k × 1 × h i × w i × d i + 1 × 1 × d i × h i × w i × d j = h i × w i × d i × ( k 2 + d j ) k×k×1×h_i×w_i×d_i +1×1×d_i×h_i×w_i×d_j=h_i×w_i×d_i×(k^2+d_j) k×k×1×hi×wi×di+1×1×di×hi×wi×dj=hi×wi×di×(k2+dj)
Inverted residual block
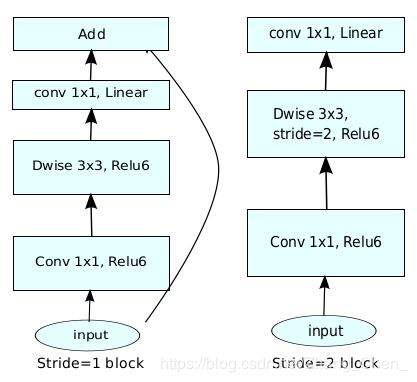 Inverted residual block的结构如上图所示,当深度可分离卷积中的深度卷积部分(图中Dwise)步长不为1的时候,不加shortcut connection。另外,当expansion ratio为1的时候,去掉最接近input的那个 1 ∗ 1 1*1 1∗1的卷积层。
Inverted residual block的结构如上图所示,当深度可分离卷积中的深度卷积部分(图中Dwise)步长不为1的时候,不加shortcut connection。另外,当expansion ratio为1的时候,去掉最接近input的那个 1 ∗ 1 1*1 1∗1的卷积层。
 Inverted:倒置的,这个block叫倒置残差的原因,是残差网络的结构是通过 1 ∗ 1 1*1 1∗1的卷积将tensor的channel降低,通过 3 ∗ 3 3*3 3∗3的卷积后,再通过 1 ∗ 1 1*1 1∗1的卷积将tensor的channel提高,而Inverted residual block的通过 1 ∗ 1 1*1 1∗1的卷积将tensor的channel提高(expansion ratio,也就是上表中的t,大于1),通过 3 ∗ 3 3*3 3∗3的卷积后,再通过 1 ∗ 1 1*1 1∗1的卷积将tensor的channel降低。
Inverted:倒置的,这个block叫倒置残差的原因,是残差网络的结构是通过 1 ∗ 1 1*1 1∗1的卷积将tensor的channel降低,通过 3 ∗ 3 3*3 3∗3的卷积后,再通过 1 ∗ 1 1*1 1∗1的卷积将tensor的channel提高,而Inverted residual block的通过 1 ∗ 1 1*1 1∗1的卷积将tensor的channel提高(expansion ratio,也就是上表中的t,大于1),通过 3 ∗ 3 3*3 3∗3的卷积后,再通过 1 ∗ 1 1*1 1∗1的卷积将tensor的channel降低。
ReLU6激活函数
ReLU6就是普通的ReLU但是限制最大输出值为6(对输出值做clip),这是为了在移动端设备float16的低精度的时候,也能有很好的数值分辨率,如果对ReLU的激活范围不加限制,输出范围为0到正无穷,如果激活值非常大,分布在一个很大的范围内,则低精度的float16无法很好地精确描述如此大范围的数值,带来精度损失。
MobileNetV2网络结构
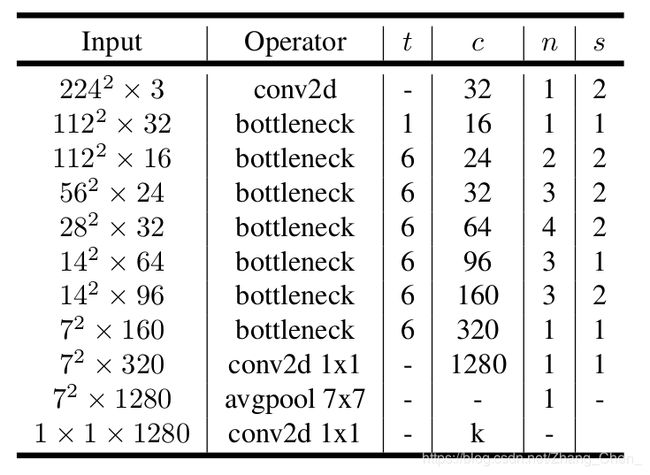 MobileNetV2的网络结构,t是Inverted residual block的expansion ratio,c是输出tensor的channel,n是block重复的次数,s是卷积步长。注意MobileNetV2对输入tensor进行了32倍下采样,是全卷积网络。
MobileNetV2的网络结构,t是Inverted residual block的expansion ratio,c是输出tensor的channel,n是block重复的次数,s是卷积步长。注意MobileNetV2对输入tensor进行了32倍下采样,是全卷积网络。
EfficientNet-B0的baseline网络结构
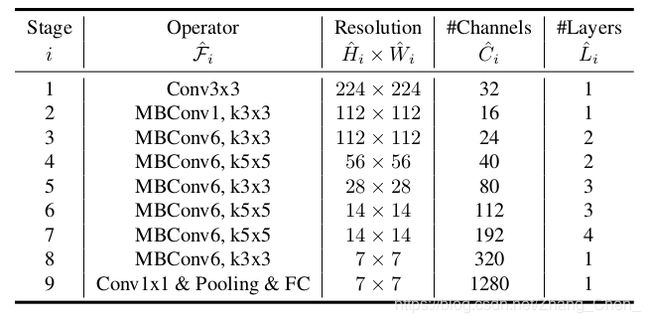 EfficientNet-B0的baseline网络结构如图所示,Resolution是输入tensor的size,#Channels是输出tensor的channel,#Layers是block重复的次数。MBConv的网络结构和MobileNetV2的Inverted residual block相同,例如:MBConv6,k3×3代表,t为6,深度卷积的卷积核尺寸为3×3。
EfficientNet-B0的baseline网络结构如图所示,Resolution是输入tensor的size,#Channels是输出tensor的channel,#Layers是block重复的次数。MBConv的网络结构和MobileNetV2的Inverted residual block相同,例如:MBConv6,k3×3代表,t为6,深度卷积的卷积核尺寸为3×3。
不同之处在于,EfficientNet-B0将ReLU6激活函数换成了Swish激活函数。另外,可以选择使用squeeze-and-excitation优化。
Swish激活函数
Swish激活函数公式为: f ( x ) = x ∗ s i g m o i d ( β x ) f(x)=x*sigmoid({\beta}x) f(x)=x∗sigmoid(βx)
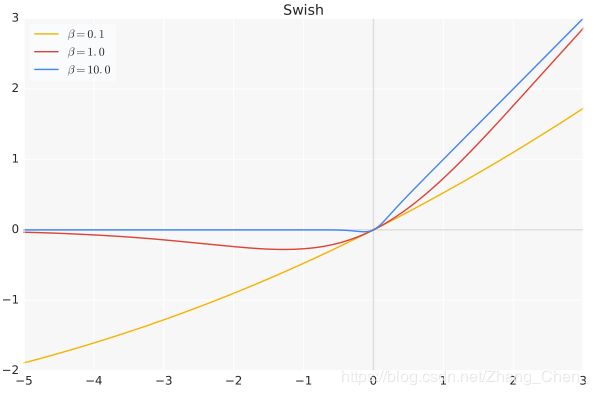 β \beta β默认为 1.0 1.0 1.0
β \beta β默认为 1.0 1.0 1.0
EfficientNet的网络scale up策略
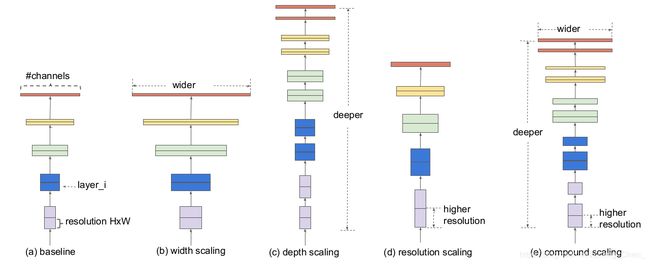
- w i d t h — — w width——w width——w:如上图 ( b ) (b) (b),通过增加baseline的channel向维度,对网络规模scale up。 w i d e r wider wider的网络能够捕获更加细粒度的特征,而且训练更容易。
- d e p t h — — d depth——d depth——d:如上图 ( c ) (c) (c),通过增加baseline的深度,也就是增加卷积层的数量,对网络规模scale up。 d e e p e r deeper deeper的网络能够捕获更丰富、更复杂的特征,但是由于梯度弥散、梯度爆炸等问题,训练难度较大。
- r e s o l u t i o n — — r resolution——r resolution——r:如上图 ( d ) (d) (d),通过增加baseline输入image的分辨率,对网络规模scale up。 h i g h e r higher higher r e s o l u t i o n resolution resolution的网络能够捕获更加细粒度的特征。
EfficientNet的网络scale up策略是:因为如果图像的分辨率更大,就需要更深的网络来提高感受野,需要更多的channel数来捕获更加细粒度的特征,因此:通过一个固定的比例对 w i d t h 、 d e p t h width、depth width、depth和 r e s o l u t i o n resolution resolution同时进行scale up,实现一个卷积神经网络中三者的平衡。也就是如上图 ( e ) (e) (e)。
scale up策略
一个卷积层可以看作一个函数:
Y i = F i ( X i ) Y_i=F_i(X_i) Yi=Fi(Xi), F i F_i Fi是卷积操作, Y i Y_i Yi是输出tensor, X i X_i Xi是输入tensor, X i X_i Xi的shape为 < H i , W i , C i >
因此一个卷积神经网络 N N N可以看作一个函数:
![]()
因为卷积神经网络可以视为几个stage的组合,每个stage重复不同的次数,而每个相同的stage的重复block都有相同的结构,所以卷积神经网络的函数可以定义如下:
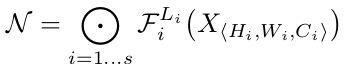
i i i是stage的索引, F i L i {F_i}^{L_i} FiLi的含义是block F i F_i Fi重复 L i L_i Li次, < H i , W i , C i >
上述中卷积神经网络的三个scale up网络规模的维度, w i d t h width width对应于增大 C i C_i Ci, d e p t h depth depth对应于增大 L i L_i Li, r e s o l u t i o n resolution resolution对应于增大 < H i , W i >
这里规定一个卷积神经网络,所有的block都按相同的比例对三个维度进行scale up,因此,scale up的优化目标可以定义为:
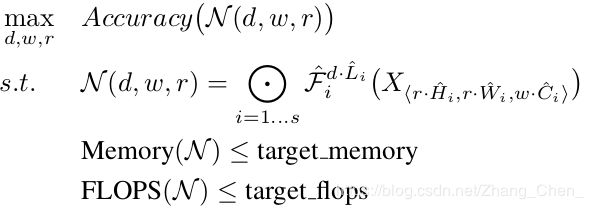
也就是在baseline的基础上,给定 d , w , r d,w,r d,w,r对卷积神经网络进行scale up,让scale up后的卷积神经网络的性能最优。
w i d t h 、 d e p t h 、 r e s o l u t i o n width、depth、resolution width、depth、resolution三个维度的scale up系数的确定方法:
- d e p t h : d = α ϕ depth:d={\alpha}^{\phi} depth:d=αϕ
- w i d t h : w = β ϕ width:w={\beta}^{\phi} width:w=βϕ
- r e s o l u t i o n : r = γ ϕ resolution:r={\gamma}^{\phi} resolution:r=γϕ
约束条件:
- α ∗ β 2 ∗ γ 2 约 等 于 2 {\alpha}*{\beta}^2*{\gamma}^2约等于2 α∗β2∗γ2约等于2
- α 、 β 、 γ 都 不 小 于 1 \alpha、\beta、\gamma都不小于1 α、β、γ都不小于1
其中, α 、 β 、 γ \alpha、\beta、\gamma α、β、γ是通过grid search得到的常数, ϕ \phi ϕ是根据计算资源的大小设置的常数。
对于EfficientNet-B0的baseline网络,固定 ϕ \phi ϕ为1,通过grid search得到 α = 1.2 \alpha=1.2 α=1.2、 β = 1.1 \beta=1.1 β=1.1、 γ = 1.15 \gamma=1.15 γ=1.15,时,scale up的卷积神经网络性能最优,得到EfficientNet-B0。
固定 α = 1.2 \alpha=1.2 α=1.2、 β = 1.1 \beta=1.1 β=1.1、 γ = 1.15 \gamma=1.15 γ=1.15,通过设置不同的 ϕ \phi ϕ值,对EfficientNet-B0的baseline网络进行scale up,进而得到EfficientNet-B1到EfficientNet-B7。
如果直接在规模更大的baseline上进行grid search得到 α \alpha α、 β \beta β和 γ \gamma γ,会得到性能更优的卷积神经网络,但是grid search需要的计算成本更大,因此,这里在小的baseline上进行grid search,然后通过修改 ϕ \phi ϕ的值,对网络进行scale up得到规模更大的卷积神经网络。
结语
如果您有修改意见或问题,欢迎留言或者通过邮箱和我联系。
手打很辛苦,如果我的文章对您有帮助,转载请注明出处。