R实现多元线性回归,主要利用的就是lm()函数
熟悉其他统计回归量的函数,对做回归分析也是很有帮助的。
- anova(m): ANOVA表
- coefficients(m): 模型的系数
- coef(m): 跟coefficients(m)一样
- confint(m): 回归系数的置信区间
- deviance(m): 残差平方和
- effects(m): 正交效应向量(Vector of orthogonal effects )
- fitted(m): 拟合的Y值向量Vector of fitted y values
- residuals(m): 模型残差Model residuals
- resid(m): 跟residuals(m)一样
- summary(m):关键统计量,例如R2、F统计量和残差标准差(σ)
- vcov(m):主参数的协防差矩阵
以下是R做多元线性回归的几个基本步骤:
1.读入数据,R-STUDIO直接有按钮,否则就
> zsj <- read.csv("D:/Paper/data/zsj.csv")
数据一般从excel的CSV或者txt里读取,实现整理好以符合R的数据框的结构
ps1:这块有很多包提供从不同来源读取数据的方法,笔者还得慢慢学。。
2.画相关图选择回归方程的形式
> plot(Y~X1);abline(lm(Y~X1))
> plot(Y~X2);abline(lm(Y~X2))
可见X1与Y的关系是明显的线性的,X2也类似此处省略
3.做回归,并检视回归结果
> lm.test<-lm(Y~X1+X2,data=zsj)
> summary(lm.test)
Call:
lm(formula = Y ~ X1 + X2, data = zsj)
Residuals:
Min 1Q Median 3Q Max
-0.21286 -0.05896 -0.01450 0.05556 0.30795
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.0931750 0.0109333 8.522 5.85e-16 ***
X1 0.0109935 0.0003711 29.625 < 2e-16 ***
X2 0.0099941 0.0010459 9.555 < 2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.08109 on 327 degrees of freedom
Multiple R-squared: 0.7953, Adjusted R-squared: 0.7941
F-statistic: 635.3 on 2 and 327 DF, p-value: < 2.2e-16
可见各项显著性检验都是得到通过的
4.用残差分析剔除异常点
> plot(lm.test,which=1:4)
得到的四个图依次为:
4.1普通残差与拟合值的残差图
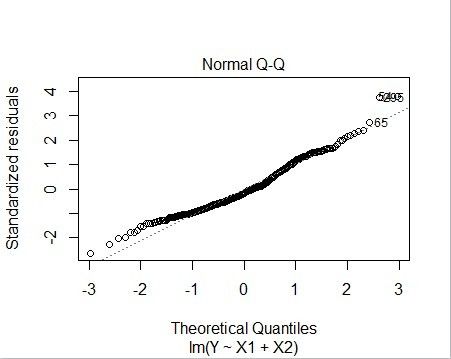
4.2正态QQ的残差图(若残差是来自正态总体分布的样本,则QQ图中的点应该在一条直线上)
4.3标准化残差开方与拟合值的残差图(对于近似服从正态分布的标准化残差,应该有95%的样本点落在[-2,2]的区间内。这也是判断异常点的直观方法)
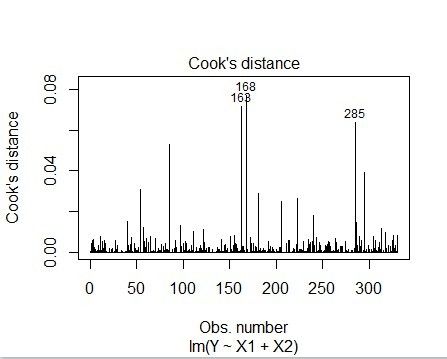
4.4cook统计量的残差图(cook统计量值越大的点越可能是异常值,但具体阀值是多少较难判别)
从图中可见,54,65,295三个样本存在异常,需要剔除。
5.检验异方差
5.1GQtest,H0(误差平方与自变量,自变量的平方和其交叉相都不相关),p值很小时拒绝H0,认为上诉公式有相关性,存在异方差
> res.test<-residuals(lm.test)
> library(lmtest)
> gqtest(lm.test)
Goldfeld-Quandt test
data: lm.test
GQ = 0.9353, df1 = 162, df2 = 162, p-value = 0.6647
5.2BPtest,H0(同方差),p值很小时认为存在异方差
> bptest(lm.test)
studentized Breusch-Pagan test
data: lm.test
BP = 3.0757, df = 2, p-value = 0.2148
两个检验都可以看出异方差不存在,不过为了总结所有情况这里还是做了一下修正。。
6.修正异方差
修正的方法选择FGLS即可行广义最小二乘
6.1修正步骤
6.1.1将y对xi求回归,算出res--u
6.1.2计算log(u^2)
6.1.3做log(u^2)对xi的辅助回归 log(u^2),得到拟合函数g=b0+b1x1+..+b2x2
6.1.4计算拟合权数1/h=1/exp(g),并以此做wls估计
> lm.test2<-lm(log(resid(lm.test)^2)~X1+X2,data=zsj)
> lm.test3<-lm(Y~X1+X2,weights=1/exp(fitted(lm.test2)),data=zsj)
> summary(lm.test3)
这里就不再贴回归结果了
7.检验多重共线性
7.1计算解释变量相关稀疏矩阵的条件数k,k<100多重共线性程度很小,1001000严重
> XX<-cor(zsj[5:6])
> kappa(XX)
[1] 2.223986
7.2寻找共线性强的解释变量组合
> eigen(XX)#用于发现共线性强的解释变量组合#
$values
[1] 1.3129577 0.6870423
$vectors
[,1] [,2]
[1,] 0.7071068 -0.7071068
[2,] 0.7071068 0.7071068
8.修正多重共线性---逐步回归法
> step(lm.test)
Start: AIC=-1655.03
Y ~ X1 + X2
Df Sum of Sq RSS AIC
- X2 1 0.6005 2.7509 -1575.8
- X1 1 5.7714 7.9218 -1226.7
Call:
lm(formula = Y ~ X1 + X2, data = zsj)
Coefficients:
(Intercept) X1 X2
0.093175 0.010994 0.009994
可见X2,X1都不去掉的时候AIC值最小,模型最佳。
ps2:step中可进行参数设置:direction=c("both","forward","backward")来选择逐步回归的方向,默认both,forward时逐渐增加解释变两个数,backward则相反。
转自:http://blog.sina.com.cn/s/blog_6ee39c3901017fpd.html
其他参考资料:
R 中使用lm进行非线性拟合
百度文库 多元回归
R学习 多元线性回归分析
R入门25招 (其中第20~24招)