CUDA编程之快速入门

CUDA（Compute Unified Device Architecture）的中文全称为计算统一设备架构。做图像视觉领域的同学多多少少都会接触到CUDA，毕竟要做性能速度优化，CUDA是个很重要的工具，CUDA是做视觉的同学难以绕过的一个坑，必须踩一踩才踏实。CUDA编程真的是入门容易精通难，具有计算机体系结构和C语言编程知识储备的同学上手CUDA编程应该难度不会很大。本文章将通过以下五个方面帮助大家比较全面地了解CUDA编程最重要的知识点，做到快速入门：

GPU架构特点
CUDA线程模型
CUDA内存模型
CUDA编程模型
CUDA应用小例子

1. GPU架构特点

首先我们先谈一谈串行计算和并行计算。我们知道，高性能计算的关键利用多核处理器进行并行计算。

当我们求解一个计算机程序任务时，我们很自然的想法就是将该任务分解成一系列小任务，把这些小任务一一完成。在串行计算时，我们的想法就是让我们的处理器每次处理一个计算任务，处理完一个计算任务后再计算下一个任务，直到所有小任务都完成了，那么这个大的程序任务也就完成了。如下图所示，就是我们怎么用串行编程思想求解问题的步骤。

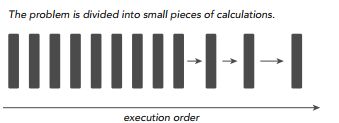
但是串行计算的缺点非常明显，如果我们拥有多核处理器，我们可以利用多核处理器同时处理多个任务时，而且这些小任务并没有关联关系（不需要相互依赖，比如我的计算任务不需要用到你的计算结果），那我们为什么还要使用串行编程呢？为了进一步加快大任务的计算速度，我们可以把一些独立的模块分配到不同的处理器上进行同时计算（这就是并行），最后再将这些结果进行整合，完成一次任务计算。下图就是将一个大的计算任务分解为小任务，然后将独立的小任务分配到不同处理器进行并行计算，最后再通过串行程序把结果汇总完成这次的总的计算任务。

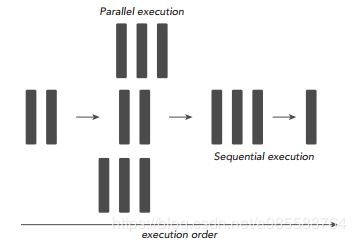
所以，一个程序可不可以进行并行计算，关键就在于我们要分析出该程序可以拆分出哪几个执行模块，这些执行模块哪些是独立的，哪些又是强依赖强耦合的，独立的模块我们可以试着设计并行计算，充分利用多核处理器的优势进一步加速我们的计算任务，强耦合模块我们就使用串行编程，利用串行+并行的编程思路完成一次高性能计算。

接下来我们谈谈CPU和GPU有什么区别，他们俩各自有什么特点，我们在谈并行、串行计算时多次谈到“多核”的概念，现在我们先从“核”的角度开始这个话题。首先CPU是专为顺序串行处理而优化的几个核心组成。而GPU则由数以千计的更小、更高效的核心组成，这些核心专门为同时处理多任务而设计，可高效地处理并行任务。也就是，CPU虽然每个核心自身能力极强，处理任务上非常强悍，无奈他核心少，在并行计算上表现不佳；反观GPU，虽然他的每个核心的计算能力不算强，但他胜在核心非常多，可以同时处理多个计算任务，在并行计算的支持上做得很好。

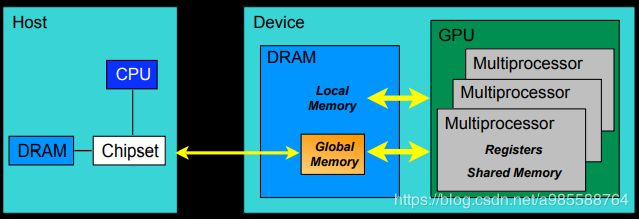
GPU和CPU的不同硬件特点决定了他们的应用场景，CPU是计算机的运算和控制的核心，GPU主要用作图形图像处理。图像在计算机呈现的形式就是矩阵，我们对图像的处理其实就是操作各种矩阵进行计算，而很多矩阵的运算其实可以做并行化，这使得图像处理可以做得很快，因此GPU在图形图像领域也有了大展拳脚的机会。下图表示的就是一个多GPU计算机硬件系统，可以看出，一个GPU内存就有很多个SP和各类内存，这些硬件都是GPU进行高效并行计算的基础。

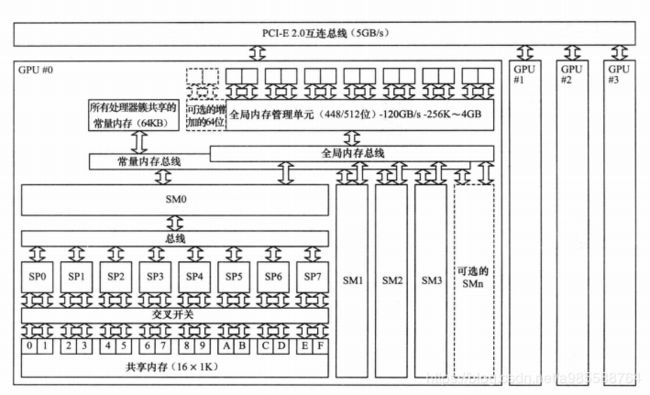
现在再从数据处理的角度来对比CPU和GPU的特点。CPU需要很强的通用性来处理各种不同的数据类型，比如整型、浮点数等，同时它又必须擅长处理逻辑判断所导致的大量分支跳转和中断处理，所以CPU其实就是一个能力很强的伙计，他能把很多事处理得妥妥当当，当然啦我们需要给他很多资源供他使用（各种硬件），这也导致了CPU不可能有太多核心（核心总数不超过16）。而GPU面对的则是类型高度统一的、相互无依赖的大规模数据和不需要被打断的纯净的计算环境，GPU有非常多核心（费米架构就有512核），虽然其核心的能力远没有CPU的核心强，但是胜在多，
在处理简单计算任务时呈现出“人多力量大”的优势，这就是并行计算的魅力。

整理一下两者特点就是：

CPU：擅长流程控制和逻辑处理，不规则数据结构，不可预测存储结构，单线程程序，分支密集型算法
GPU：擅长数据并行计算，规则数据结构，可预测存储模式

现在的计算机体系架构中，要完成CUDA并行计算，单靠GPU一人之力是不能完成计算任务的，必须借助CPU来协同配合完成一次高性能的并行计算任务。

一般而言，并行部分在GPU上运行，串行部分在CPU运行，这就是异构计算。具体一点，异构计算的意思就是不同体系结构的处理器相互协作完成计算任务。CPU负责总体的程序流程，而GPU负责具体的计算任务，当GPU各个线程完成计算任务后，我们就将GPU那边计算得到的结果拷贝到CPU端，完成一次计算任务。

所以应用程序利用GPU实现加速的总体分工就是：密集计算代码（约占5%的代码量）由GPU负责完成，剩余串行代码由CPU负责执行。
2. CUDA线程模型

CUDA软件层次结构
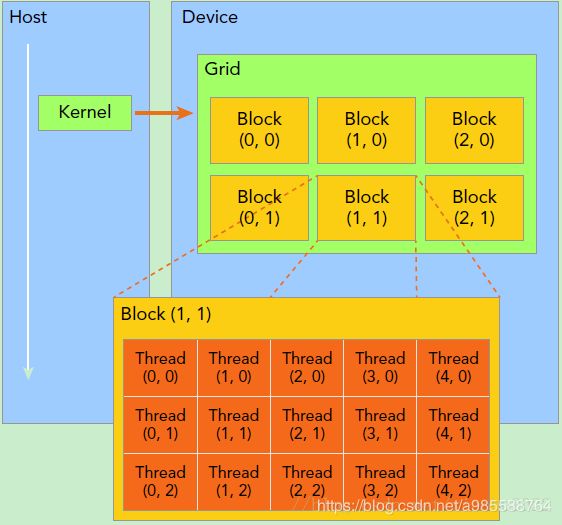
下面我们介绍CUDA的线程组织结构。首先我们都知道，线程是程序执行的最基本单元，CUDA的并行计算就是通过成千上万个线程的并行执行来实现的。下面的机构图说明了GPU的不同层次的结构。

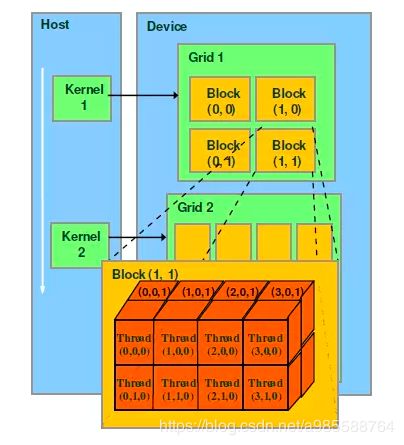
CUDA的线程模型从小往大来总结就是：

Thread：线程，并行的基本单位
Thread Block：线程块，互相合作的线程组，线程块有如下几个特点：

允许彼此同步
可以通过共享内存快速交换数据
以1维、2维或3维组织

Grid：一组线程块

以1维、2维组织
共享全局内存

Kernel：在GPU上执行的核心程序，这个kernel函数是运行在某个Grid上的。

One kernel <-> One Grid

每一个block和每个thread都有自己的ID，我们通过相应的索引找到相应的线程和线程块。

threadIdx，blockIdx
Block ID: 1D or 2D
Thread ID: 1D, 2D or 3D

理解kernel，必须要对kernel的线程层次结构有一个清晰的认识。首先GPU上很多并行化的轻量级线程。kernel在device上执行时实际上是启动很多线程，一个kernel所启动的所有线程称为一个网格（grid），同一个网格上的线程共享相同的全局内存空间，grid是线程结构的第一层次，而网格又可以分为很多线程块（block），一个线程块里面包含很多线程，这是第二个层次。线程两层组织结构如上图所示，这是一个gird和block均为2-dim的线程组织。grid和block都是定义为dim3类型的变量，dim3可以看成是包含三个无符号整数（x，y，z）成员的结构体变量，在定义时，缺省值初始化为1。因此grid和block可以灵活地定义为1-dim，2-dim以及3-dim结构，kernel调用时也必须通过执行配置<<>>来指定kernel所使用的网格维度和线程块维度。举个例子，我们以上图为例，分析怎么通过<<>>>这种标记方式索引到我们想要的那个线程。CUDA的这种<<>>其实就是一个多级索引的方法，第一级索引是(grid.xIdx, grid.yIdy)，对应上图例子就是(1, 1)，通过它我们就能找到了这个线程块的位置，然后我们启动二级索引(block.xIdx, block.yIdx, block.zIdx)来定位到指定的线程。这就是我们CUDA的线程组织结构。

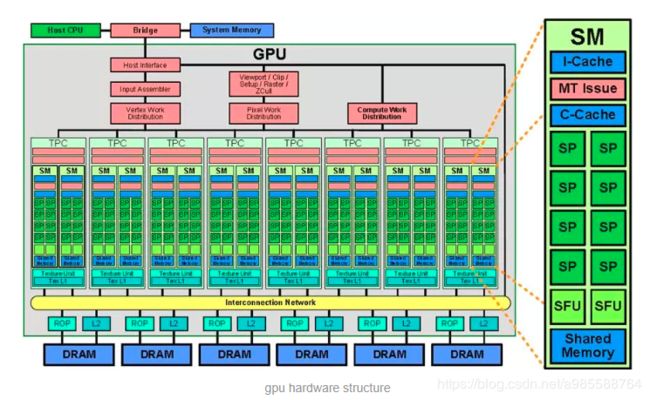
这里想谈谈SP和SM（流处理器），很多人会被这两个专业名词搞得晕头转向。

SP：最基本的处理单元，streaming processor，也称为CUDA core。最后具体的指令和任务都是在SP上处理的。GPU进行并行计算，也就是很多个SP同时做处理。
SM：多个SP加上其他的一些资源组成一个streaming multiprocessor。也叫GPU大核，其他资源如：warp scheduler，register，shared memory等。SM可以看做GPU的心脏（对比CPU核心），register和shared memory是SM的稀缺资源。CUDA将这些资源分配给所有驻留在SM中的threads。因此，这些有限的资源就使每个SM中active warps有非常严格的限制，也就限制了并行能力。

需要指出，每个SM包含的SP数量依据GPU架构而不同，Fermi架构GF100是32个，GF10X是48个，Kepler架构都是192个，Maxwell都是128个。

简而言之，SP是线程执行的硬件单位，SM中包含多个SP，一个GPU可以有多个SM（比如16个），最终一个GPU可能包含有上千个SP。这么多核心“同时运行”，速度可想而知，这个引号只是想表明实际上，软件逻辑上是所有SP是并行的，但是物理上并不是所有SP都能同时执行计算（比如我们只有8个SM却有1024个线程块需要调度处理），因为有些会处于挂起，就绪等其他状态，这有关GPU的线程调度。

下面这个图将从硬件角度和软件角度解释CUDA的线程模型。

每个线程由每个线程处理器（SP）执行
线程块由多核处理器（SM）执行
一个kernel其实由一个grid来执行，一个kernel一次只能在一个GPU上执行

cuda异构编程模型
block是软件概念，一个block只会由一个sm调度，程序员在开发时，通过设定block的属性，告诉GPU硬件，我有多少个线程，线程怎么组织。而具体怎么调度由sm的warps scheduler负责，block一旦被分配好SM，该block就会一直驻留在该SM中，直到执行结束。一个SM可以同时拥有多个blocks，但需要序列执行。下图显示了GPU内部的硬件架构：

3. CUDA内存模型

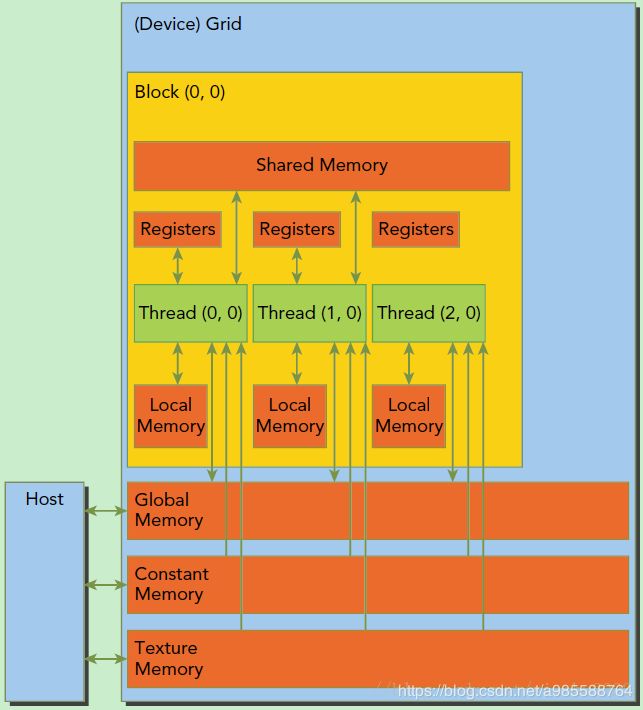
CUDA中的内存模型分为以下几个层次：

每个线程都用自己的registers（寄存器）
每个线程都有自己的local memory（局部内存）
每个线程块内都有自己的shared memory（共享内存），所有线程块内的所有线程共享这段内存资源
每个grid都有自己的global memory（全局内存），不同线程块的线程都可使用
每个grid都有自己的constant memory（常量内存）和texture memory（纹理内存），），不同线程块的线程都可使用

线程访问这几类存储器的速度是register > local memory >shared memory > global memory

下面这幅图表示就是这些内存在计算机架构中的所在层次。

4. CUDA编程模型

上面讲了这么多硬件相关的知识点，现在终于可以开始说说CUDA是怎么写程序的了。
在CUDA程序构架中，主程序还是由 CPU 来执行，而当遇到数据并行处理的部分，CUDA 就会将程序编译成 GPU 能执行的程序，并传送到GPU。而这个程序在CUDA里称做核（kernel）。CUDA允许程序员定义称为核的C语言函数，从而扩展了 C 语言，在调用此类函数时，它将由N个不同的CUDA线程并行执行N次，这与普通的C语言函数只执行一次的方式不同。执行核的每个线程都会被分配一个独特的线程ID，可通过内置的threadIdx变量在内核中访问此ID。

在 CUDA 程序中，主程序在调用任何 GPU 内核之前，必须对核进行执行配置，即确定线程块数和每个线程块中的线程数以及共享内存大小。

CUDA编程模型是一个异构模型，需要CPU和GPU协同工作。在CUDA中，host和device是两个重要的概念，我们用host指代CPU及其内存，而用device指代GPU及其内存。CUDA程序中既包含host程序，又包含device程序，它们分别在CPU和GPU上运行。同时，host与device之间可以进行通信，这样它们之间可以进行数据拷贝。典型的CUDA程序的执行流程如下：

分配host内存，并进行数据初始化；
分配device内存，并从host将数据拷贝到device上；
调用CUDA的核函数在device上完成指定的运算；
将device上的运算结果拷贝到host上；
释放device和host上分配的内存。

上面流程中最重要的一个过程是调用CUDA的核函数来执行并行计算，kernel是CUDA中一个重要的概念，kernel是在device上线程中并行执行的函数，核函数用__global__符号声明，在调用时需要用<<>>来指定kernel要执行的线程数量，在CUDA中，每一个线程都要执行核函数，并且每个线程会分配一个唯一的线程号thread ID，这个ID值可以通过核函数的内置变量threadIdx来获得。

由于GPU实际上是异构模型，所以需要区分host和device上的代码，在CUDA中是通过函数类型限定词开区别host和device上的函数，主要的三个函数类型限定词如下：

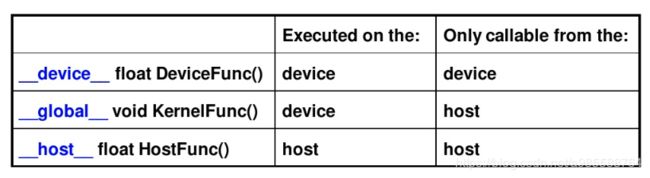
__global__：在device上执行，从host中调用（一些特定的GPU也可以从device上调用），返回类型必须是void，不支持可变参数参数，不能成为类成员函数。注意用__global__定义的kernel是异步的，这意味着host不会等待kernel执行完就执行下一步。
__device__：在device上执行，单仅可以从device中调用，不可以和__global__同时用。
__host__：在host上执行，仅可以从host上调用，一般省略不写，不可以和__global__同时用，但可和__device__，此时函数会在device和host都编译。

要深刻理解kernel，必须要对kernel的线程层次结构有一个清晰的认识。首先GPU上很多并行化的轻量级线程。kernel在device上执行时实际上是启动很多线程，一个kernel所启动的所有线程称为一个网格（grid），同一个网格上的线程共享相同的全局内存空间，grid是线程结构的第一层次，而网格又可以分为很多线程块（block），一个线程块里面包含很多线程，这是第二个层次。线程两层组织结构如下图所示，这是一个gird和block均为2-dim的线程组织。grid和block都是定义为dim3类型的变量，dim3可以看成是包含三个无符号整数（x，y，z）成员的结构体变量，在定义时，缺省值初始化为1。因此grid和block可以灵活地定义为1-dim，2-dim以及3-dim结构，对于图中结构（主要水平方向为x轴），定义的grid和block如下所示，kernel在调用时也必须通过执行配置<<>>来指定kernel所使用的线程数及结构。
dim3 grid(3, 2);
dim3 block(5, 3);
kernel_fun<<< grid, block >>>(prams…);

执行配置运算符<<<>>>，用来传递内核函数的执行参数。格式如下：
kernel<<>>(para1, para2, …);

gridDim表示网格的大小，可以是1,2,3维
blockDim表示块的·大小，可以是1,2,3维
memSize表示动态分配的共享存储器大小，默认为0
stream表示执行的流，默认为0
para1, para2等为核函数参数

#include

global void func(int a, int b) {
}

int main() {
int a = 0, b = 0;
func<<<128, 128>>>(a, b);
func<<>>(a, b);
func<<>>(a, b);
return 0;
}

kernel以线程网格（Grid）的形式组织，每个线程网格由若干个线程块（block）组成，而每个线程块又由若干个线程（thread）组成，但是block之间不能相互通信，也没有执行顺序,但是同一个block里面的线程可以相互通信，在一个block里面，有shared memory，并通过栅栏同步保证线程间能够正确地共享数据。具体来说，可以在kernel函数中通过设置_syncthreads()函数实现。

内建变量使用了dim3类型，所谓dim3是基于uint3定义的矢量类型

对于一维的block，线程的threadID就是threadIdx.x

对于二维的block(Dx,Dy)，线程的threadID就是threadIdx.x+threadIdx.y*Dx

对于三维的block(Dx,Dy,Dz)的三维block，线程的threadID是threadIdx.x+threadIdx.yDx+threadIdx.zDx*Dy

threadIdx，顾名思义获取线程thread的ID索引；如果线程是一维的那么就取threadIdx.x，二维的还可以多取到一个值threadIdx.y，以此类推到三维threadIdx.z。
blockIdx，线程块的ID索引；同样有blockIdx.x，blockIdx.y，blockIdx.z。
blockDim，线程块的维度，同样有blockDim.x，blockDim.y，blockDim.z。
gridDim，线程格的维度，同样有gridDim.x，gridDim.y，gridDim.z。
对于一维的block，线程的threadID=threadIdx.x。
对于大小为（blockDim.x, blockDim.y）的 二维 block，线程的threadID=threadIdx.x+threadIdx.yblockDim.x。
对于大小为（blockDim.x, blockDim.y, blockDim.z）的 三维 block，线程的threadID=threadIdx.x+threadIdx.yblockDim.x+threadIdx.zblockDim.xblockDim.y。

核函数只能在主机端调用，其调用形式为：Kernel<<>>(param list)

Dg：用于定义整个grid的维度和尺寸，即一个grid有多少个block。为dim3类型。Dim3 Dg(Dg.x, Dg.y, 1)表示grid中每行有Dg.x个block，每列有Dg.y个block，第三维恒为1(目前一个核函数只有一个grid)。整个grid中共有Dg.x*Dg.y个block，其中Dg.x和Dg.y最大值为65535。
Db：用于定义一个block的维度和尺寸，即一个block有多少个thread。为dim3类型。Dim3 Db(Db.x, Db.y, Db.z)表示整个block中每行有Db.x个thread，每列有Db.y个thread，高度为Db.z。Db.x和Db.y最大值为512，Db.z最大值为62。一个block中共有Db.xDb.yDb.z个thread。计算能力为1.0,1.1的硬件该乘积的最大值为768，计算能力为1.2,1.3的硬件支持的最大值为1024。
Ns：是一个可选参数，用于设置每个block除了静态分配的shared Memory以外，最多能动态分配的shared memory大小，单位为byte。不需要动态分配时该值为0或省略不写。
S：是一个cudaStream_t类型的可选参数，初始值为零，表示该核函数处在哪个流之中。

所以，一个线程需要两个内置的坐标变量（blockIdx，threadIdx）来唯一标识，它们都是dim3类型变量，其中blockIdx指明线程所在grid中的位置，而threaIdx指明线程所在block中的位置，如图中的Thread (1,1)满足：

threadIdx.x = 1
threadIdx.y = 1
blockIdx.x = 1
blockIdx.y = 1

一个线程块上的线程是放在同一个流式多处理器（SM)上的，但是单个SM的资源有限，这导致线程块中的线程数是有限制的，现代GPUs的线程块可支持的线程数可达1024个。有时候，我们要知道一个线程在blcok中的全局ID，此时就必须还要知道block的组织结构，这是通过线程的内置变量blockDim来获得。它获取线程块各个维度的大小。对于一个2-dim的block(Dx,Dy)
，线程(x,y)的ID值为(x+y∗Dx)，如果是3-dim的block(Dx,Dy,Dz)，线程(x,y,z)的ID值为(x+y∗Dx+z∗Dx∗Dy)

。另外线程还有内置变量gridDim，用于获得网格块各个维度的大小。

kernel的这种线程组织结构天然适合vector,matrix等运算，如我们将利用上图2-dim结构实现两个矩阵的加法，每个线程负责处理每个位置的两个元素相加，代码如下所示。线程块大小为(16, 16)，然后将N*N大小的矩阵均分为不同的线程块来执行加法运算。
// Kernel定义
global void MatAdd(float A[N][N], float B[N][N], float C[N][N])
{
int i = blockIdx.x * blockDim.x + threadIdx.x;
int j = blockIdx.y * blockDim.y + threadIdx.y;
if (i < N && j < N)
C[i][j] = A[i][j] + B[i][j];
}
int main()
{
…
// Kernel 线程配置
dim3 threadsPerBlock(16, 16);
dim3 numBlocks(N / threadsPerBlock.x, N / threadsPerBlock.y);
// kernel调用
MatAdd<<>>(A, B, C);
…
}
此外这里简单介绍一下CUDA的内存模型，如下图所示。可以看到，每个线程有自己的私有本地内存（Local Memory），而每个线程块有包含共享内存（Shared Memory）,可以被线程块中所有线程共享，其生命周期与线程块一致。此外，所有的线程都可以访问全局内存（Global Memory）。还可以访问一些只读内存块：常量内存（Constant Memory）和纹理内存（Texture Memory）。内存结构涉及到程序优化，这里不深入探讨它们。

还有重要一点，你需要对GPU的硬件实现有一个基本的认识。上面说到了kernel的线程组织层次，那么一个kernel实际上会启动很多线程，这些线程是逻辑上并行的，但是在物理层却并不一定。这其实和CPU的多线程有类似之处，多线程如果没有多核支持，在物理层也是无法实现并行的。但是好在GPU存在很多CUDA核心，充分利用CUDA核心可以充分发挥GPU的并行计算能力。GPU硬件的一个核心组件是SM，前面已经说过，SM是英文名是 Streaming Multiprocessor，翻译过来就是流式多处理器。SM的核心组件包括CUDA核心，共享内存，寄存器等，SM可以并发地执行数百个线程，并发能力就取决于SM所拥有的资源数。当一个kernel被执行时，它的gird中的线程块被分配到SM上，一个线程块只能在一个SM上被调度。SM一般可以调度多个线程块，这要看SM本身的能力。那么有可能一个kernel的各个线程块被分配多个SM，所以grid只是逻辑层，而SM才是执行的物理层。SM采用的是SIMT (Single-Instruction, Multiple-Thread，单指令多线程)架构，基本的执行单元是线程束（wraps)，线程束包含32个线程，这些线程同时执行相同的指令，但是每个线程都包含自己的指令地址计数器和寄存器状态，也有自己独立的执行路径。所以尽管线程束中的线程同时从同一程序地址执行，但是可能具有不同的行为，比如遇到了分支结构，一些线程可能进入这个分支，但是另外一些有可能不执行，它们只能死等，因为GPU规定线程束中所有线程在同一周期执行相同的指令，线程束分化会导致性能下降。当线程块被划分到某个SM上时，它将进一步划分为多个线程束，因为这才是SM的基本执行单元，但是一个SM同时并发的线程束数是有限的。这是因为资源限制，SM要为每个线程块分配共享内存，而也要为每个线程束中的线程分配独立的寄存器。所以SM的配置会影响其所支持的线程块和线程束并发数量。总之，就是网格和线程块只是逻辑划分，一个kernel的所有线程其实在物理层是不一定同时并发的。所以kernel的grid和block的配置不同，性能会出现差异，这点是要特别注意的。还有，由于SM的基本执行单元是包含32个线程的线程束，所以block大小一般要设置为32的倍数。
我们先捋一捋常见的CUDA术语：

第一个要掌握的编程要点：我们怎么写一个能在GPU跑的程序或函数呢？

通过关键字就可以表示某个程序在CPU上跑还是在GPU上跑！如下表所示，比如我们用__global__定义一个kernel函数，就是CPU上调用，GPU上执行，注意__global__函数的返回值必须设置为void。

第二个编程要点：CPU和GPU间的数据传输怎么写？

首先介绍在GPU内存分配回收内存的函数接口：

cudaMalloc(): 在设备端分配global memory
cudaFree(): 释放存储空间

CPU的数据和GPU端数据做数据传输的函数接口是一样的，他们通过传递的函数实参（枚举类型）来表示传输方向：

cudaMemcpy(void dst, void src, size_t nbytes,
enum cudaMemcpyKind direction)

enum cudaMemcpyKind:

cudaMemcpyHostToDevice（CPU到GPU）
cudaMemcpyDeviceToHost（GPU到CPU）
cudaMemcpyDeviceToDevice（GPU到GPU）

第三个编程要点是：怎么用代码表示线程组织模型？
我们可以用dim3类来表示网格和线程块的组织方式，网格grid可以表示为一维和二维格式，线程块block可以表示为一维、二维和三维的数据格式。

dim3 DimGrid(100, 50); //5000个线程块，维度是10050
dim3 DimBlock(4, 8, 8); //每个线层块内包含256个线程，线程块内的维度是48*8

接下来介绍一个非常重要又很难懂的一个知识点，我们怎么计算线程号呢？
1.使用N个线程块，每一个线程块只有一个线程，即

dim3 dimGrid(N);
dim3 dimBlock(1);

此时的线程号的计算方式就是

threadId = blockIdx.x;

其中threadId的取值范围为0到N-1。对于这种情况，我们可以将其看作是一个列向量，列向量中的每一行对应一个线程块。列向量中每一行只有1个元素，对应一个线程。
2.使用M×N个线程块，每个线程块1个线程

由于线程块是2维的，故可以看做是一个M*N的2维矩阵，其线程号有两个维度，即：

dim3 dimGrid(M,N);
dim3 dimBlock(1);

其中

blockIdx.x 取值0到M-1
blcokIdx.y 取值0到N-1

这种情况一般用于处理2维数据结构，比如2维图像。每一个像素用一个线程来处理，此时需要线程号来映射图像像素的对应位置，如

pos = blockIdx.y * blcokDim.x + blockIdx.x; //其中gridDim.x等于M

3.使用一个线程块，该线程具有N个线程，即

dim3 dimGrid(1);
dim3 dimBlock(N);

此时线程号的计算方式为

threadId = threadIdx.x;

其中threadId的范围是0到N-1，对于这种情况，可以看做是一个行向量，行向量中的每一个元素的每一个元素对应着一个线程。
4.使用M个线程块，每个线程块内含有N个线程，即

dim3 dimGrid(M);
dim3 dimBlock(N);

这种情况，可以把它想象成二维矩阵，矩阵的行与线程块对应，矩阵的列与线程编号对应，那线程号的计算方式为

threadId = threadIdx.x + blcokIdx*blockDim.x;

上面其实就是把二维的索引空间转换为一维索引空间的过程。
5.使用M×N的二维线程块，每一个线程块具有P×Q个线程，即

dim3 dimGrid(M, N);
dim3 dimBlock(P, Q);

这种情况其实是我们遇到的最多情况，特别适用于处理具有二维数据结构的算法，比如图像处理领域。

其索引有两个维度

threadId.x = blockIdx.xblockDim.x+threadIdx.x;
threadId.y = blockIdx.yblockDim.y+threadIdx.y;

上述公式就是把线程和线程块的索引映射为图像像素坐标的计算方法。
CUDA应用例子

我们已经掌握了CUDA编程的基本语法，现在我们开始以一些小例子来真正上手CUDA。

首先我们编写一个程序，查看我们GPU的一些硬件配置情况。

#include “device_launch_parameters.h”
#include

int main()
{
int deviceCount;
cudaGetDeviceCount(&deviceCount);
for(int i=0;i {
cudaDeviceProp devProp;
cudaGetDeviceProperties(&devProp, i);
std::cout << "使用GPU device " << i << ": " << devProp.name << std::endl;
std::cout << “设备全局内存总量： " << devProp.totalGlobalMem / 1024 / 1024 << “MB” << std::endl;
std::cout << “SM的数量：” << devProp.multiProcessorCount << std::endl;
std::cout << “每个线程块的共享内存大小：” << devProp.sharedMemPerBlock / 1024.0 << " KB” << std::endl;
std::cout << “每个线程块的最大线程数：” << devProp.maxThreadsPerBlock << std::endl;
std::cout << "设备上一个线程块（Block）种可用的32位寄存器数量： " << devProp.regsPerBlock << std::endl;
std::cout << “每个EM的最大线程数：” << devProp.maxThreadsPerMultiProcessor << std::endl;
std::cout << “每个EM的最大线程束数：” << devProp.maxThreadsPerMultiProcessor / 32 << std::endl;
std::cout << "设备上多处理器的数量： " << devProp.multiProcessorCount << std::endl;
std::cout << “======================================================” << std::endl;

}
return 0;

}

我们利用nvcc来编译程序。

nvcc test1.cu -o test1

输出结果：因为我的服务器是8个TITAN GPU，为了省略重复信息，下面只显示两个GPU结果

使用GPU device 0: TITAN X (Pascal)
设备全局内存总量： 12189MB
SM的数量：28
每个线程块的共享内存大小：48 KB
每个线程块的最大线程数：1024
设备上一个线程块（Block）种可用的32位寄存器数量： 65536
每个EM的最大线程数：2048
每个EM的最大线程束数：64设备上多处理器的数量： 28

使用GPU device 1: TITAN X (Pascal)
设备全局内存总量： 12189MB
SM的数量：28
每个线程块的共享内存大小：48 KB
每个线程块的最大线程数：1024
设备上一个线程块（Block）种可用的32位寄存器数量： 65536
每个EM的最大线程数：2048
每个EM的最大线程束数：64
设备上多处理器的数量： 28

…

第一个计算任务：将两个元素数目为1024×1024的float数组相加。

首先我们思考一下如果只用CPU我们怎么串行完成这个任务。

#include
#include
#include
#include

using namespace std;

int main()
{
struct timeval start, end;
gettimeofday( &start, NULL );
floatA, B, C;
int n = 1024 * 1024;
int size = n * sizeof(float);
A = (float)malloc(size);
B = (float)malloc(size);
C = (float)malloc(size);

for(int i=0;i

}

CPU方式输出结果

max_error is 0
total time is 22ms

如果我们使用GPU来做并行计算，速度将会如何呢？

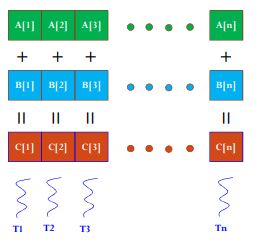
编程要点：

每个Block中的Thread数最大不超过512；
为了充分利用SM，Block数尽可能多，>100。

#include “cuda_runtime.h”
#include
#include
#include

using namespace std;

global void Plus(float A[], float B[], float C[], int n)
{
int i = blockDim.x * blockIdx.x + threadIdx.x;
C[i] = A[i] + B[i];
}

int main()
{
struct timeval start, end;
gettimeofday( &start, NULL );
float*A, *Ad, *B, *Bd, *C, *Cd;
int n = 1024 * 1024;
int size = n * sizeof(float);

// CPU端分配内存
A = (float*)malloc(size);
B = (float*)malloc(size);
C = (float*)malloc(size);

// 初始化数组
for(int i=0;i>>(Ad, Bd, Cd, n);

// 将在GPU端计算好的结果拷贝回CPU端
cudaMemcpy(C, Cd, size, cudaMemcpyDeviceToHost);

// 校验误差
float max_error = 0.0;
for(int i=0;i

}

GPU方式输出结果

max error is 0
total time is 1278ms

由上面的例子看出，使用CUDA编程时我们看不到for循环了，因为CPU编程的循环已经被分散到各个thread上做了，所以我们也就看到不到for一类的语句。从结果上看，CPU的循环计算的速度比GPU计算快多了，原因就在于CUDA中有大量的内存拷贝操作（数据传输花费了大量时间，而计算时间却非常少），如果计算量比较小的话，CPU计算会更合适一些。

下面计算一个稍微复杂的例子，矩阵加法，即对两个矩阵对应坐标的元素相加后的结果存储在第三个的对应位置的元素上。

值得注意的是，这个计算任务我采用了二维数组的计算方式，注意一下二维数组在CUDA编程中的写法。

CPU版本

#include
#include
#include
#include

#define ROWS 1024
#define COLS 1024

using namespace std;

int main()
{
struct timeval start, end;
gettimeofday( &start, NULL );
int A, A_ptr, B, **B_ptr, C, **C_ptr;
int total_size = ROWSCOLSsizeof(int);
A = (int)malloc(total_size);
B = (int)malloc(total_size);
C = (int)malloc(total_size);
A_ptr = (int**)malloc(ROWSsizeof(int));
B_ptr = (int**)malloc(ROWSsizeof(int));
C_ptr = (int**)malloc(ROWSsizeof(int));

//CPU一维数组初始化
for(int i=0;i

}

CPU方式输出

max_error is 0
total time is 29ms

GPU版本

#include “cuda_runtime.h”
#include “device_launch_parameters.h”
#include
#include
#include
#define Row 1024
#define Col 1024

global void addKernel(int **C, int **A, int ** B)
{
int idx = threadIdx.x + blockDim.x * blockIdx.x;
int idy = threadIdx.y + blockDim.y * blockIdx.y;
if (idx < Col && idy < Row) {
C[idy][idx] = A[idy][idx] + B[idy][idx];
}
}

int main()
{
struct timeval start, end;
gettimeofday( &start, NULL );

int **A = (int **)malloc(sizeof(int*) * Row);
int **B = (int **)malloc(sizeof(int*) * Row);
int **C = (int **)malloc(sizeof(int*) * Row);
int *dataA = (int *)malloc(sizeof(int) * Row * Col);
int *dataB = (int *)malloc(sizeof(int) * Row * Col);
int *dataC = (int *)malloc(sizeof(int) * Row * Col);
int **d_A;
int **d_B;
int **d_C;
int *d_dataA;
int *d_dataB;
int *d_dataC;
//malloc device memory
cudaMalloc((void**)&d_A, sizeof(int **) * Row);
cudaMalloc((void**)&d_B, sizeof(int **) * Row);
cudaMalloc((void**)&d_C, sizeof(int **) * Row);
cudaMalloc((void**)&d_dataA, sizeof(int) *Row*Col);
cudaMalloc((void**)&d_dataB, sizeof(int) *Row*Col);
cudaMalloc((void**)&d_dataC, sizeof(int) *Row*Col);
//set value
for (int i = 0; i < Row*Col; i++) {
    dataA[i] = 90;
    dataB[i] = 10;
}
//将主机指针A指向设备数据位置，目的是让设备二级指针能够指向设备数据一级指针
//A 和  dataA 都传到了设备上，但是二者还没有建立对应关系
for (int i = 0; i < Row; i++) {
    A[i] = d_dataA + Col * i;
    B[i] = d_dataB + Col * i;
    C[i] = d_dataC + Col * i;
}
                                                            
cudaMemcpy(d_A, A, sizeof(int*) * Row, cudaMemcpyHostToDevice);
cudaMemcpy(d_B, B, sizeof(int*) * Row, cudaMemcpyHostToDevice);
cudaMemcpy(d_C, C, sizeof(int*) * Row, cudaMemcpyHostToDevice);
cudaMemcpy(d_dataA, dataA, sizeof(int) * Row * Col, cudaMemcpyHostToDevice);
cudaMemcpy(d_dataB, dataB, sizeof(int) * Row * Col, cudaMemcpyHostToDevice);
dim3 threadPerBlock(16, 16);
dim3 blockNumber( (Col + threadPerBlock.x - 1)/ threadPerBlock.x, (Row + threadPerBlock.y - 1) / threadPerBlock.y );
printf("Block(%d,%d)   Grid(%d,%d).\n", threadPerBlock.x, threadPerBlock.y, blockNumber.x, blockNumber.y);
addKernel << > > (d_C, d_A, d_B);
//拷贝计算数据-一级数据指针
cudaMemcpy(dataC, d_dataC, sizeof(int) * Row * Col, cudaMemcpyDeviceToHost);
                                                                                         
int max_error = 0;
for(int i=0;i

}

GPU输出

Block(16,16) Grid(64,64).
max_error is 0
total time is 442 ms

从结果看出，CPU计算时间还是比GPU的计算时间短。这里需要指出的是，这种二维数组的程序写法的效率并不高（虽然比较符合我们的思维方式），因为我们做了两次访存操作。所以一般而言，做高性能计算一般不会采取这种编程方式。

最后一个例子我们将计算一个更加复杂的任务，矩阵乘法

回顾一下矩阵乘法：两矩阵相乘，左矩阵第一行乘以右矩阵第一列（分别相乘，第一个数乘第一个数），乘完之后相加，即为结果的第一行第一列的数，依次往下算，直到计算完所有矩阵元素。

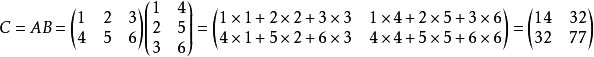
CPU版本

#include
#include
#include

#define ROWS 1024
#define COLS 1024

using namespace std;

void matrix_mul_cpu(float* M, float* N, float* P, int width)
{
for(int i=0;i for(int j=0;j {
float sum = 0.0;
for(int k=0;k {
float a = M[iwidth+k];
float b = N[kwidth+j];
sum += ab;
}
P[iwidth+j] = sum;
}
}

int main()
{
struct timeval start, end;
gettimeofday( &start, NULL );
float A, B, C;
int total_size = ROWSCOLSsizeof(float);
A = (float)malloc(total_size);
B = (float*)malloc(total_size);
C = (float*)malloc(total_size);

//CPU一维数组初始化
for(int i=0;i

}

CPU输出

total time is 7617ms

梳理一下CUDA求解矩阵乘法的思路：因为C=A×B，我们利用每个线程求解C矩阵每个(x, y)的元素，每个线程载入A的一行和B的一列，遍历各自行列元素，对A、B对应的元素做一次乘法和一次加法。

GPU版本

#include “cuda_runtime.h”
#include “device_launch_parameters.h”
#include
#include
#include
#define Row 1024
#define Col 1024

global void matrix_mul_gpu(int M, int N, int* P, int width)
{
int i = threadIdx.x + blockDim.x * blockIdx.x;
int j = threadIdx.y + blockDim.y * blockIdx.y;

int sum = 0;
for(int k=0;k

}

int main()
{
struct timeval start, end;
gettimeofday( &start, NULL );

int *A = (int *)malloc(sizeof(int) * Row * Col);
int *B = (int *)malloc(sizeof(int) * Row * Col);
int *C = (int *)malloc(sizeof(int) * Row * Col);
//malloc device memory
int *d_dataA, *d_dataB, *d_dataC;
cudaMalloc((void**)&d_dataA, sizeof(int) *Row*Col);
cudaMalloc((void**)&d_dataB, sizeof(int) *Row*Col);
cudaMalloc((void**)&d_dataC, sizeof(int) *Row*Col);
//set value
for (int i = 0; i < Row*Col; i++) {
    A[i] = 90;
    B[i] = 10;
}
                                                            
cudaMemcpy(d_dataA, A, sizeof(int) * Row * Col, cudaMemcpyHostToDevice);
cudaMemcpy(d_dataB, B, sizeof(int) * Row * Col, cudaMemcpyHostToDevice);
dim3 threadPerBlock(16, 16);
dim3 blockNumber((Col+threadPerBlock.x-1)/ threadPerBlock.x, (Row+threadPerBlock.y-1)/ threadPerBlock.y );
printf("Block(%d,%d)   Grid(%d,%d).\n", threadPerBlock.x, threadPerBlock.y, blockNumber.x, blockNumber.y);
matrix_mul_gpu << > > (d_dataA, d_dataB, d_dataC, Col);
//拷贝计算数据-一级数据指针
cudaMemcpy(C, d_dataC, sizeof(int) * Row * Col, cudaMemcpyDeviceToHost);
                                                                                         
//释放内存
free(A);
free(B);
free(C);
cudaFree(d_dataA);
cudaFree(d_dataB);
cudaFree(d_dataC);

gettimeofday( &end, NULL );
int timeuse = 1000000 * ( end.tv_sec - start.tv_sec ) + end.tv_usec - start.tv_usec;
printf("total time is %d ms\n", timeuse/1000);

return 0;

}

GPU输出

Block(16,16) Grid(64,64).
total time is 506 ms

从这个矩阵乘法任务可以看出，我们通过GPU进行并行计算的方式仅花费了0.5秒，但是CPU串行计算方式却花费了7.6秒，计算速度提升了十多倍，可见并行计算的威力！