XGBoost简单推导及理解

前言

XGBoost的全称是eXtreme Gradient Boosting。作为一个非常有效的机器学习方法，Boosting Tree是数据挖掘和机器学习中最常用的算法之一。因为它效果好，对于输入要求不敏感，相对LR 的优势如不需要做特征的归一化，自动进行特征选择，模型可解释性较好，可以适应多种损失函数如 SquareLoss，LogLoss 等，往往是从统计学家到数据科学家必备的工具之一，它同时也是kaggle比赛冠军选手最常用的工具。最后，因为它的效果好，在计算速度和准确率上，较GBDT有明显的提升计算复杂度不高，也在工业界中有大量的应用。

前置知识：GBDT

模型函数形式

给定数据集 D=(xi,yi) D = ( x i , y i ) ,XGBoost进行additive training，学习 K K 棵树，采用以下函数对样本进行预测：

y^i=ϕ(xi)=∑k=1Kfk(xi),fk∈F y ^ i = ϕ ( x i ) = ∑ k = 1 K f k ( x i ) , f k ∈ F

这里 F F 是假设空间， f(x) f ( x ) 是CART回归树

F={f(x)=wq(x)}(q:Rm→T,w∈RT) F = { f ( x ) = w q ( x ) } ( q : R m → T , w ∈ R T )

注意：这里 q(x) q ( x ) 表示将样本x分到了某个叶子节点上，w是叶子节点的分数（leaf score），所以 wq(x) w q ( x ) 表示回归树对样本的预测值。这些定义在之后会用到。

目标函数

XGBoost的目标函数（函数空间）为

L(ϕ)=∑i=1Nl(yi,y^i)+Ω(fk) L ( ϕ ) = ∑ i = 1 N l ( y i , y ^ i ) + Ω ( f k )

其中 l(yi,y^i) l ( y i , y ^ i ) 为误差函数， Ω(fk) Ω ( f k ) 为正则项，对每棵回归树的复杂度进行了惩罚。

那么有哪些指标可以衡量树的复杂度？

• 树的深度，内部节点个数，叶子节点个数(T)，叶节点分数(w)..
• XGBoost用的是
  
  Ω(fk)=γT+12λ||w||2 Ω ( f k ) = γ T + 1 2 λ | | w | | 2
  
  对叶子节点个数和叶节点分数进行惩罚，相当于在训练过程中做了剪枝。

误差函数的泰勒二阶展开

第t次迭代之后，模型的的预测等于前t-1次的模型预测加上第t棵树的预测：

y^(t)i=y^(t−1)i+ft(xi) y ^ i ( t ) = y ^ i ( t − 1 ) + f t ( x i )

此时目标函数可写作：

L(t)=∑i=1nl(yi,y^(t−1)i+ft(xi))+Ω(ft) L ( t ) = ∑ i = 1 n l ( y i , y ^ i ( t − 1 ) + f t ( x i ) ) + Ω ( f t )

公式中 yi,y^(t−1)i y i , y ^ i ( t − 1 ) 都已知，模型要学习的只有第t棵树 ft f t
将误差函数在 y^(t−1)i y ^ i ( t − 1 ) 处进行二阶泰勒展开：

L(t)≈∑i=1nl(yi,y^(t−1)i)+gift(xi)+12hif2t(xi)+Ω(ft) L ( t ) ≈ ∑ i = 1 n l ( y i , y ^ i ( t − 1 ) ) + g i f t ( x i ) + 1 2 h i f t 2 ( x i ) + Ω ( f t )

其中
gi=∂y^(t−1)l(yi,y^(t−1)i) g i = ∂ y ^ ( t − 1 ) l ( y i , y ^ i ( t − 1 ) ) hi=∂2y^(t−1)l(yi,y^(t−1)i) h i = ∂ y ^ ( t − 1 ) 2 l ( y i , y ^ i ( t − 1 ) )

将公式中的常数项去掉，得到:

L^(t)=∑i=1n[gift(xi)+12hif2t(xi)]+Ω(ft) L ^ ( t ) = ∑ i = 1 n [ g i f t ( x i ) + 1 2 h i f t 2 ( x i ) ] + Ω ( f t )

把 ft,Ω(ft) f t , Ω ( f t ) 写成树结构的形式，即把下式代入目标函数中
f(x)=wq(x) f ( x ) = w q ( x ) Ω(f)=γT+12λ||w||2 Ω ( f ) = γ T + 1 2 λ | | w | | 2

得到：

L^(t)=∑i=1n[giwq(xi)+12hiw2q(xi)]+γT+λ12∑j=1Tw2j L ^ ( t ) = ∑ i = 1 n [ g i w q ( x i ) + 1 2 h i w q ( x i ) 2 ] + γ T + λ 1 2 ∑ j = 1 T w j 2

其中 ∑ni=1[giwq(xi)+12hiw2q(xi)] ∑ i = 1 n [ g i w q ( x i ) + 1 2 h i w q ( x i ) 2 ] 是对样本累加， λ12∑Tj=1w2j λ 1 2 ∑ j = 1 T w j 2 是对叶节点累加。

统一起来：定义每个叶节点j上的样本集合为 Ij={i|q(xi)=j} I j = { i | q ( x i ) = j }
则目标函数可以写成按叶节点累加的形式：

L^(t)=∑j=1T[(∑i∈Ijgi)wj+12(∑i∈IJhi+λ)w2j]+γT=∑j=1T[(Gjwj+12(Hj+λ)w2j]+γT L ^ ( t ) = ∑ j = 1 T [ ( ∑ i ∈ I j g i ) w j + 1 2 ( ∑ i ∈ I J h i + λ ) w j 2 ] + γ T = ∑ j = 1 T [ ( G j w j + 1 2 ( H j + λ ) w j 2 ] + γ T

如果确定了树的结构（即 q(x) q ( x ) 确定），为了使目标函数最小，可以令其导数为0，解得每个叶节点的最优预测分数为:

w∗j=−GjHj+λ w j ∗ = − G j H j + λ

代入目标函数，得到最小损失为：

L^∗=−12∑j=1TG2jHj+λ+γT L ^ ∗ = − 1 2 ∑ j = 1 T G j 2 H j + λ + γ T

学习策略

ID3算法采用信息增益
C4.5算法采用信息增益比
CART分类树采用Gini系数

在XGBoost中，参考上式， G2jHj+λ G j 2 H j + λ 部分衡量了每个叶子节点对总体损失的的贡献，我们希望损失越小越好，则标红部分的值越大越好。

因此，对一个叶子节点进行分裂，分裂前后的增益定义为：
Gain=G2LHL+λ+G2RHR+λ−(G2L+GR)2HL+HR+λ−γ G a i n = G L 2 H L + λ + G R 2 H R + λ − ( G L 2 + G R ) 2 H L + H R + λ − γ
Gain的值越大，分裂后 L 减小越多。所以当对一个叶节点分割时，计算所有候选(feature,value)对应的Gain，选取Gain最大的进行分割。

树节点分裂方法(Split Finding)

• 精确算法:遍历所有特征的所有可能的分割点，计算gain值，选取值最大的（feature，value）去分割
  

• 近似算法: 对于每个特征，只考察分位点，减少计算复杂度
  
  • Global：学习每棵树前，提出候选切分点
  • Local：每次分裂前，重新提出候选切分点

  实际上XGBoost不是简单地按照样本个数进行分位，而是以二阶导数值作为权重(Weighted Quantile Sketch)

稀疏值处理

当特征出现缺失值时，XGBoost可以学习出默认的节点分裂方向。

其他特性

1. 行抽样，列抽样(借鉴随机森林) ：降低过拟合，减少计算
2. 支持自定义损失函数(需二阶可导)
3. Shrinkage：每次迭代会将叶子节点权重乘以系数，削弱每棵树影响
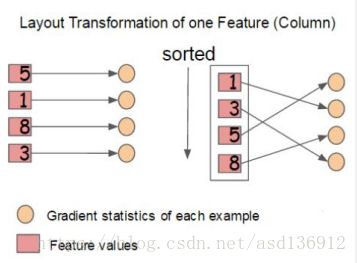
4. 支持并行：XGBoost的并行是在特征粒度上的。我们知道，决策树的学习最耗时的一个步骤就是对特征的值进行排序（因为要确定最佳分割点），XGBoost在训练之前，预先对数据进行了排序，然后保存为block结构，后面的迭代中重复地使用这个结构，大大减小计算量。这个block结构也使得并行成为了可能，在进行节点的分裂时，需要计算每个特征的增益，最终选增益最大的那个特征去做分裂，那么各个特征的增益计算就可以开多线程进行。

5. 可并行的近似直方图算法：树节点在进行分裂时，我们需要计算每个特征的每个分割点对应的增益，即用贪心法枚举所有可能的分割点。当数据无法一次载入内存或者在分布式情况下，贪心算法效率就会变得很低，所以xgboost还提出了一种可并行的近似直方图算法，用于高效地生成候选的分割点。

   把连续的浮点特征值离散化成k个整数，同时构造一个宽度为k的直方图。在
   遍历数据的时候，根据离散化后的值作为索引在直方图中累积统计量，当遍
   历一次数据后，直方图累积了需要的统计量，然后根据直方图的离散值，遍
   历寻找最优的分割点。
   
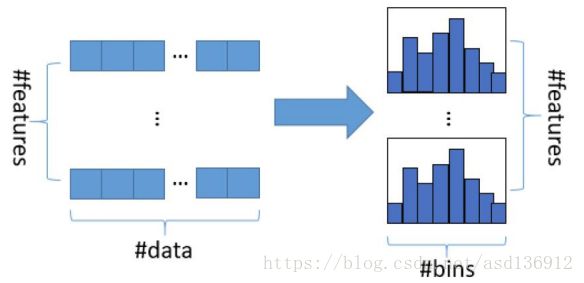
   • 减小内存占用，比如离散为256个bin时，只需要8bit，节省7/8
   • 减小了split finding时计算增益的计算量， 从O(#data)

系统设计

• Column Block

  • 特征预排序，以column block的结构存于内存中。
  • 存储样本索引（instance indices）
  • block中的数据以稀疏格式（CSC）存储

  这个结构加速了split finding的过程，只需要在建树前排序一次，后面节点分裂时直接根据索引得到梯度信息

• Cache Aware Access

  • column block按特征大小顺序存储，相应的样本的梯度信息是分散的，造成内存的不连续访问，降低CPU cache 命中率。
  • 缓存优化方法
    
    • 预取数据到buffer中（非连续->连续），再统计梯度信息
    • 调节块的大小

参考

1. http://www.52cs.org/?p=429
2. https://blog.csdn.net/a819825294/article/details/51206410
3. http://pan.baidu.com/s/1gfA6FK3
4. http://learningsys.org/papers/LearningSys_2015_paper_32.pdf
5. acm=1488265641_ffdebf36cef2b1bf7f3f76abf6bfe426”>http://delivery.acm.org/10.1145/2940000/2939785/p785-chen.pdf?ip=202.118.228.100&id=2939785&acc=ACTIVE%20SERVICE&key=BF85BBA5741FDC6E.5C4511229FC427D6.4D4702B0C3E38B35.4D4702B0C3E38B35&CFID=905733202&CFTOKEN=53852884&acm=1488265641_ffdebf36cef2b1bf7f3f76abf6bfe426