记录一下个人看了王小草深度学习笔记之后的理解，目录如下，

0. Overview
1. 逻辑回归
2. 神经元感知器
3. DNN vs CNN vs RNN
4. CNN
   - 输入层
     - 去均值
     - 归一化
     - PCA
     - 白化
   - 卷积计算层
   - 激励层
     - sigmoid
     - tanh
     - RELU
     - Leaky RELU
     - ELU
     - Maxout
     - 激励层经验
   - 池化层
   - 全连接层
   - 输出层
5. 循环神经网络
   - 双向RNN
   - 深层双向RNN
6. 循环神经网络之LSTM
7. 权重初始化
8. 正则化与dropout
9. 最优化与参数更新
10. 深度学习在IoT大数据和流分析中的应用

Overview

先来看看人工智能Artificial intelligence，数据挖掘Data Mining，机械学习Machine learning，深度学习Deep learning之间的关系，

AI Set

人工智能知识图谱

1 逻辑回归

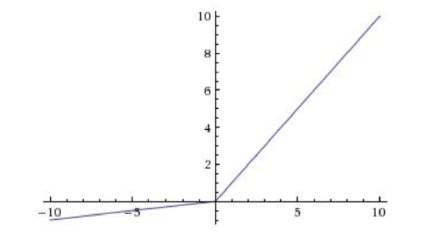
首先，将特征输入到一个一元或多元的linear函数z中，

Linear

然后将这个线性函数z作为一个输入，输入到sigmoid函数g(z)中，

Sigmoid

值域

根据图形，可以更清晰地看到，

当z < 0，则g(z) < 0.5
当z > 0，则g(z) > 0.5
因此它可以作为一个二元的分类器，大于0.5的判为正类，小于0.5的判为负类。

2 神经元感知器

之所以在这里提及逻辑回归，因为逻辑回归激活函数sigmoid可以当成神经元中的感知器。下图中，最左侧就是输入z函数的变量（或者叫特征或因子），1为常量bias，x1,x2为两个特征。从这三个变量到z有三条边，分别是权重，也就是逻辑回归z函数里的系数，将变量与对应的系数相乘并线性相加的过程就是线性函数z的求解过程，通过这一步，我们求出了z。从中间的小圆z到右边的小圆a，就是逻辑回归的第二步了，即将z作为输入变量代入g(z)中，求解出g(z)或a。

神经元的感知

当添加少量的隐藏层，简单的感知器就变成了一个浅层神经网了（SNN），从上一层到下一层就是一个感知器，

浅层神经网络SNN

如果添加更多的隐藏层，就形成了一个深层神经网了（DNN），包含了多个感知器，

深层神经网络DNN

3 DNN vs CNN vs RNN

DNN是一个大类，CNN是一个典型的空间上深度的神经网络，RNN是在时间上深度的神经网络。

4 CNN

卷积神经网在神经网络的基础上有所变化。下图中，每一列都表示一个层级，这些层级的类型不同，有INPUT，CONV，RELU，POOL，FC，SOFTMAX。这些层的结构与功能下面会详细说。

4.1 数据输入层 INPUT

输入层我们可以看做是对数据做的预处理，数据的预处理使得输入数据的质量增高，从而也能配合模型做最优的结果。预处理的方式有如下几种：

4.1.1 去均值

去均值就是将输入数据的各个维度都中心化到0。求出原始数据的均值，然后将每个数据减去均值，计算后的新数据均值就变成0了。下图中直观可见，就是将数据的分布平移到以0为中心（每个特征的均值都是0），
x_new = x_old - avg(x_old)

去均值

4.1.2 归一化

归一化/标准化/正则化是将特征的幅度变换到统一范围（不一定是0-1之间）。通常有min-max标准化和Z-score标准化方法。这个在图像识别中不使用，这里只是拿出来说一下，因为图像的RGB本来就是在0-255之间，幅度是一样的，故不需要做调整。由下图是归一化后的数据，

归一化

4.1.3 PCA

PCA是主成分分析，一种降维的方法，经常被使用，可以解决共线性（特征之间彼此相关），同时也降低了维度，简化了模型，提高了模型的性价比，

PCA

4.1.4 白化

白化其实是指将特征转换成正态分布，

白化

4.2 卷积计算层 CONV

首先假设图像上的某个像素点与和它向邻近的点是相似的，也就是对于图像上的某块小区域，区域内的点因为相近，所以相似，

基于这个假设，某个神经元就可以只对这一块小区域做连线，但不是对整个小区域做一根连线，而是对整个区域中的每个点做连接。这个小区域会移动的，它从左到右移动，然后向下一行再从左到右移动，将这个图片都遍历一遍，每一次移动都只是对新的小区域内的点做连接

CNN1

18+51+121+35+204=429

CNN2

在卷积层，假设每个神经元连接数据窗口的权重是一致的的，即权重共享机制。
因为对于每个神经元它们的分工是独立相异的。比如，第一个神经元负责记录图像的颜色特征，第二个神经元负责关注图片的轮廓信息，第三个神经元负责关注图像的纹理特征…也就是说每个神经元只负责关注一个特性。

单个神经元用于提取某一个特征，而单个神经元内权重共享；如果需要提取更多的特征，引入更多的神经元，神经元之间权重不共享，神经元内权重共享。图CNN1和CNN2都只是展示了一个神经元的感知过程，即权重共享。

另外，因为权重共享机制，权重的维度便大大地降低了。一组固定的权重与不同窗口内的数据做内积的过程，就叫做“卷积”。

4.3 激励层

激励层的功能就是把卷基层输出的结果做一个非线性的映射。
非线性的映射就是将线性函数的输出结果作为一个输入变量放进sigmoid函数中，输出的值范围就在[0,1]之间了。
在卷计算机网的激励层，就是将卷积层的输出作为输入变量放进一个函数中，从而做一个非线性的转换。

激励层的函数有多种，

4.3.1 sigmoid

sigmoid

4.3.2 tanh

Tanh是与sigmoid类似的，也是呈现一个S型，但中心店为0

tanh

4.3.3 RELU

The Rectified Linear Unit/修正线性单元，RELU是卷计神经网络中最常用的激励函数

RELU

4.3.4 Leaky RELU

这也是一个由两条射线组成的函数，与RELU不同的是，当x<0时，形成的是一条斜率为a的射线。
这样保证了无论x取什么值，都会求到不等于0的斜率，在SGD反向传播时避免了”饱和”,而且计算得也很快。

Leaky RELU

4.3.5 ELU

指数线性单元，
当x > 0 时，仍然与前两个激励函数相同
当x < 0 时，时一条在x轴下方y轴左边的指数函数

ELU

4.3.6 Maxout

maxout

由函数可见Maxout也是由两条直线拼接起来的，计算是线性的，但是引入了更多的参数。

4.3.7 激励层经验

不要用sigmoid
首先试RELU，因为快
如果RELU失败，使用Leaky RELU或者Maxout
在某些特殊领域下，tanh较好

4.4 池化层 pooling

池化层是夹在连续的卷基层中间的（卷基层中包含了激励层）

池化层的过程非常简单，就是将数据进行压缩，类似输入层的线性输入是权重加和，而这里是只取mask的最大值/均值/最小值，

pooling

这个过程叫做downsampling，向下取样。有两个优点，

压缩了数据和参数的量
缓解了过拟合

4.5 全连接层 FC

全连接的方式其实就是深度神经网络中的连接方式。通常全连接层放在卷积神经网络的尾部。

之所以在最后还要使用全连接是为了还原信息。虽然全连接会增加非常多的参数以及计算的复杂度，但是只在最后一层进行全连接还是可以承受的，况且它可以还原更多信息量，总体而言“性价比”比较高。

4.6 输出层

CNN后面接的输出层，

分类问题，softmax
回归问题，cross entropy交叉熵

5 循环神经网络

它是一种具有记忆的神经网络，工业界最常见的应用，如机器翻译。另外，一切与序列或时间相关的问题都可以用RNN来尝试一下，比如RNN模型能写文章写代码写诗歌写乐谱等等。即上下文context的应用环境。

RNN中引入了记忆的概念。输出依赖于输入和上一个时间点的记忆。记忆功能使得前文中的东西仍然对后文产生了影响。

RNN1

上图的右边部分：从左到右是时间发展的过程，第一个是t-1的时刻，中间是t时刻，第三个是t+1时刻。St是t时刻的记忆，x是指输入，O是指输出，W是指从上一个时刻t-1到这个时刻t的权重，U是指输入到隐层的权重。

很直观的看到，在t时刻，St被两个箭头所指向，分别是来自于t-1时刻的St-1 * W的影响，和t时刻的输入Xt * U的影响。也就是说，和传统的神经网络相比，RNN多了一份对过去的记忆。

RNN2

f可以是tanh等的激励函数，输入激励函数的分别是这个时刻的输入乘以权重，和前一个时刻的记忆乘以权重。

5.1 双向RNN

存在这样的情况，当前的输出不仅仅依赖于之前的序列元素，还可能依赖之后的序列元素，比如完形填空题，可能需要去看看下文在讲什么，才能知道前面的空格填什么。此时就需要双向循环神经网络。

双向RNN

5.2 深层双向RNN

深层双向RNN和双向RNN的区别是每一步，也就是每一个时间点我们设置了多层结构。

深层双向RNN

6 循环神经网络之LSTM

前面RNN中提到了，RNN虽然有记忆，但是随着时间间隔不断增大，RNN会丧失学习到连接如此远的信息的能力。也就是说，记忆容量有限，一本书从头到尾一字不漏去记，肯定离得越远的东西忘得越多。这主要是因为在BPTT后向求导的时候，偏导数会越来越接近于0，从而丧失记忆。

LSTM是RNN中的一种类型，大体的结构与RNN是几乎一样的。而区别在于：

LSTM的记忆细胞是改造过的
LSTM实现了一种功能，就是该记的信息会一直传递下去，不该记的信息会被门gate给截断不往下传

LSTM1

LSTM cell1

LSTM cell2

门类型，

忘记门，决定细胞状态中需要丢弃什么信息，这些信息对之后的计算和预测都是没有用的，所以趁早舍弃掉，不要占用大脑资源也避免了对后续信息的误导
输入门，将一些对后文有用的新的信息添加到细胞状态中
输出门，将上面两个门的结果作用合起来

7 权重初始化

神经网络的训练的有两种方式，第一种是自己从头到尾训练一遍；第二种是使用别人训练好的模型，然后根据自己的实际需求做改动与调整。后者我们叫做fine-tuning。在model zoo有大量训练好的模型。

权重的初始值设置得太大或者太小都不适合
于是Xavier在2010年发表论文提出了一种解决办法。z值是由于上级指向它的节点Xi乘以对应的权重的总和。也就是说，影响z值大小的有两个因素：输入层节点的个数，权重值。为了平衡这两个因素，我们认为当输入节点很多的时候，相应的初始权重应当小一点；当节点比较的时候，初始权重应当相应增大
但是方差仍然随着神经网络层次的深入变得越来越小，在10层处已经接近于0了，这表示，该层各个神经元的输出值非常相近，出现了梯度弥散。将之前输入节点n的开根号，还成n/2的开根号，表示每一此过激励函数都会被斩掉一半的输出，也就是下层激励函数的输入，既然节点数被斩掉了一半，那么自然权重应该相对应地增加了
batch normalization

8 正则化与dropout

8.1 正则化

我们的目的并不是得到一个模型去和训练数据完全拟合，而是需要这个模型能够对所有数据都有一个良好地拟合。
对训练数据过于精确地拟合反而对其他数据就不那么精确了。就像量身定制的衣服只适合于一个人，而通用的S,M,L码对大部分人都是可以适合的

L1正则化
L2正则化
L1+L2
最大范数约束

但其实在神经网络中很少用正则化的方式去避免过拟合，原因如下：
1.神经网络中的权重w非常多，对每个权重都去加上λ|w|，会使计算变复杂。
2.在正则化中产生了一个超参数λ，是需要人为却设定的，它的大小会影响模型的训练。

8.2 dropuut

它的原理是不一次性开启所有学习单元。
如下图，左图中的是全链接的神经网络，会非常精确地去训练与预测，右图却中关闭了一些神经元。也就是说别让你的神经元去记忆所有东东，要有一些泛化能力。也可以理解为，不要让你的神经网络去听信一家之言，对不同的模型做一个融合。（因为每个batch过来关闭掉的节点是不同的）

dropout

9 最优化与参数更新

只要学习率很小，就能保证loss一直减小，但是收敛会非常慢

动量更新Momentum update
Nesterov Momentum
学习率衰减
- 步伐衰减
- 指数衰减
- 1/t衰减

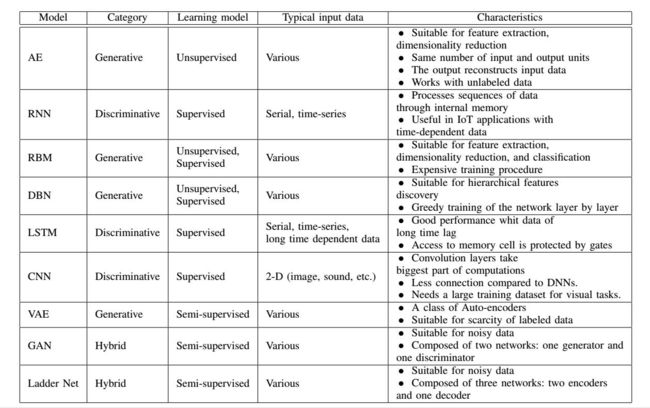
10 深度学习在IoT大数据和流分析中的应用

深度学习模型总结

自动编码器（Autoencoders，AE）
循环神经网络（Recurrent Neural Networks，RNN）
受限玻尔兹曼机（Restricted Boltzmann Machine，RBM）
深度信念网络（Deep Belief Network，DBN）
长短时记忆（Long Short Term Memory，LSTM）
卷积神经网络(Convolutional Neural Networks，CNN)
变分自动编码器（Variational Autoencoders，VAE）
生成对抗网络（Generative Adversarial Networks，GAN）
阶梯网络（Ladder Network）

深度学习框架总结

深度学习Note