通信基础概念（三）相关与正交
相关与正交
\;\;\,\quad 简单地说，一般而言，相关指的是有联系，对信号而言，相关就是相似，正交就是不相似。
\;\;\,\quad 事实上，相关(correlation)、依赖(dependent)、独立(independent)、正交(orthogonal)是统计学上的概念，通过不同随机变量之间的统计量关系来定义的，和本文中讨论的“相关”和“正交”非常不同。事实上，在通信和信号处理领域，“相关”和“正交”的概念只是与统计中的idea类似，更接近于线代中的向量相似度和正交概念。
\;\;\,\quad p.s.本文依然不够严谨，严谨的数学解释请参看概率论课本、信号与系统课程中有关信号的矢量空间分析一章。
\;\;\,\quad 线性代数中的相关与正交含义。线性相关——某个矢量可用有限个其他矢量的线性组合所表示。 举个例子，定义一个月内支出向量的各元素为 [总支出,第1周支出,第2周支出,第3周支出,第4周支出] ，这几个元素（也可以看成是1x1矢量）之间是线性相关的，因为总支出等于各周支出之和。这么看来，总支出就是一个“多余”的元素，而四周的支出相互之间没有关联（就这么假设着吧），是线性无关的，也可以叫做正交。注意，这个例子说的是物理意义上的相关与正交，物理上是正交的在数学上也可能可以看是相关的。如上面的例子可能对应以下这组数据（两行表示有两个人的数据）
[ 100 20 20 20 20 50 10 10 10 10 ] = [ a 1 → , a 2 → , a 3 → , a 4 → , a 5 → ] \left[ \begin{matrix} 100 & 20 & 20 & 20 & 20 \\ 50 & 10 & 10 & 10 & 10 \end{matrix} \right] =\left[ \overrightarrow{a_1} , \overrightarrow{a_2} , \overrightarrow{a_3} , \overrightarrow{a_4} , \overrightarrow{a_5} \right] [100502010201020102010]=[a1,a2,a3,a4,a5]那么在数学上，除了有 a 1 → = ∑ i = 2 5 a i → \overrightarrow{a_1}=\sum_{i=2}^5{ \overrightarrow{a_i} } a1=∑i=25ai这个线性组合关系，还有 a 2 → = a 3 → = a 4 → = a 5 → \overrightarrow{a_2}=\overrightarrow{a_3}=\overrightarrow{a_4}=\overrightarrow{a_5} a2=a3=a4=a5这个线性组合关系，那么后面那四个向量在数学意义上就不是正交的。在信号处理或者分析过程中，常常会出现像这样的，物理意义和数学关系不是一一对应的情况，甚至有些数学运算是没有物理意义的，只是起一个工具的作用去帮助我们做简化。
\;\;\,\quad 信号中的相关与正交。 通常我们说两个事物相关，从统计的角度上，指的是他们之间有一定的因果关系。然而，任意给定两个信号，它们之间并不会有因果关系，那么为什么要引入“相关”这个词呢？它有什么用？它具体的含义又是什么呢？
\;\;\,\quad 想象一下这个场景，课间休息时，你想告诉同学中午去吃猪脚饭，刚好在说“猪脚饭”这三个字的时候，旁边有个人突然咳嗽，使得对方只听到你的语调而听不清具体的字。正当他想让你重新说一次的时候，老师要上课了。他就只能根据语调去猜测你说了什么，和平常常去的地方作比较，比如“一食堂”、“黄焖鸡”、“金拱门”，想了想发现和“猪脚饭”读音最相近，就最终确定了这个信息。
\;\;\,\quad 这就是信号相关的含义所在。信号传输的过程中，不可避免地会有噪声，有时噪声甚至还会把原信号淹没掉，而当发送端没有足够的资源再一次发送相同的信号时，接收端就只能根据所接收的噪声信号进行信息还原。在上面的例子中，与可能信号比较然后取相似程度最高的方式，在通信系统中叫做相关接收1。这里“相关”就指的是两者之间的相似性。
\;\;\,\quad 相关函数。上面是人主观上对信号相似性进行判别的例子，那么对于机器来说要怎么判别呢？这必须有一个定量的标准，也就是说要借助数学工具去对信号做一些运算。加？减？乘？除？幂？取对数？哪些可以哪些不行？为什么？如果有多种组合都可以达到目标，要选哪一种？在计算向量的相似度时，有许多方法，比如最简单的两个向量相减，求它们的距离；又或者是求它们的内积（一个向量在另一个向量方向上的投影）。在计算信号相似性的时候可不可以也这样做呢？
\;\;\,\quad 把接收到的信号看作关于时间的函数，或是一个序列。为了能一眼看出来相关性的大小，我们希望最后得到的结果是一个数。一个序列→一个数，很自然的，我们会想到用求和/积分的方法，那么计算相似性的公式就应该有这样的结构： R = ∫ g ( t ) d t = ∫ g ( f 1 ( t ) , f 2 ( t ) ) d t R=\int{g(t)}dt=\int{g(f_1 (t),f_2 (t))}dt R=∫g(t)dt=∫g(f1(t),f2(t))dt。接下来我们要想的就是这个 g ( t ) g(t) g(t)内对两个信号 f 1 ( t ) , f 2 ( t ) f_1 (t),f_2 (t) f1(t),f2(t)采用什么运算。最简单的想法是 f 1 ( t ) − f 2 ( t ) f_1 (t)-f_2 (t) f1(t)−f2(t)，或者再加个绝对值表示距离；也可以 f 1 ( t ) ⋅ f 2 ( t ) f_1 (t)·f_2 (t) f1(t)⋅f2(t)，类似于内积运算，哪个更好呢？不如做个matlab仿真看一下吧：
\;\;\,\quad 先看原始信号，做一个感觉上的判断， f 1 f_1 f1和 f 3 f_3 f3应该是相似度比较高的，虽然反转了过来（负相关）；而 f 1 f_1 f1和 f 2 f_2 f2根本没有相似性，可以看作是正交的。那么哪种运算于我们直观的感受更加符合呢？相减求和的运算量虽然很少，但是从求和的结果并不能直接看出相关性，是数值越大越相关呢还是越小越相关呢？也看不出正相关和负相关的关系。相比之下，使用乘法的出来的结果就好看多了。因此在这两种计算方法中，我们选择乘法。当然，还可以有其他的算法，那就要另外再做比较了。
\;\;\,\quad 由此，我们得到了相关性的计算式： R = ∫ g ( t ) d t = ∫ f 1 ( t ) ⋅ f 2 ( t ) d t R=\int{g(t)}dt=\int{f_1 (t)·f_2 (t)}dt R=∫g(t)dt=∫f1(t)⋅f2(t)dt（这其实是函数内积的定义）。而在实际系统中，接收到的信号会与原信号有一个时间上的延时，记为 τ \tau τ，那么更普遍的相关函数的表达式就是2：
R ( τ ) = ∫ − ∞ + ∞ f 1 ( t ) ⋅ f 2 ( t − τ ) d t = ∫ − ∞ + ∞ f 1 ( t + τ ) ⋅ f 2 ( t ) d t R(\tau)=\int_{-\infty}^{+\infty}{f_1 (t)·f_2 (t-\tau)}dt=\int_{-\infty}^{+\infty}{f_1 (t+\tau)·f_2 (t)}dt R(τ)=∫−∞+∞f1(t)⋅f2(t−τ)dt=∫−∞+∞f1(t+τ)⋅f2(t)dt \;\;\,\quad 正事做完了，让我们再看看下面三个丑爆了的图。如果不标颜色的话，从图上已经完全看不出哪个对应哪个原始信号了。这时我们算一下加噪信号与原信号 f 1 f_1 f1的相关性（右下），从计算结果（图例）可以神奇地发现，算出来的数竟然和上面那个没有噪声的差不了多少！Bingo！通过这种相关接收的方式，我们可以在一定程度上忽视噪声的影响，得到我们想要的结果。
\;\;\,\quad 正交。有了上述相关的概念，正交就很容易理解了。在几何中，当两条直线相互垂直时正交，或者是两个面相互垂直时正交，更一般的说法就是投影值为0。在线性代数中，一个向量到另一个相量的投影从内积去表示。信号正交也可以这样定义： 当 f 1 ( t ) 与 f 2 ( t ) 在 区 间 [ t 1 , t 2 ] 上 的 内 积 ⟨ f 1 , f 2 ⟩ = ∫ t 1 t 2 f 1 ( t ) ⋅ f 2 ( t ) d t = 0 时 ， 它 们 在 该 区 间 上 正 交 。 当f_1 (t)与f_2 (t)在区间[t_1,t_2]上的内积\langle{f_1,f_2}\rangle=\int_{t_1}^{t_2}{f_1 (t)·f_2 (t)}dt=0时，它们在该区间上正交。 当f1(t)与f2(t)在区间[t1,t2]上的内积⟨f1,f2⟩=∫t1t2f1(t)⋅f2(t)dt=0时，它们在该区间上正交。
\;\;\,\quad 正交函数集。请先思考一个问题，如果要求使用最少的资源，将本文前部举的关于线性相关的例子中的信息发送出去，你会选择怎么发？从物理意义上说，因为总支出与各周支出之间是有一个求和关系的，所以只需要把每周支出和求和关系发送出去就可以了。从数学上说，可以看到在这个具体例子中， a 2 → = a 3 → = a 4 → = a 5 → \overrightarrow{a_2}=\overrightarrow{a_3}=\overrightarrow{a_4}=\overrightarrow{a_5} a2=a3=a4=a5，那么就可以更简单一点，只把 a 5 → \overrightarrow{a_5} a5和相等关系、求和关系发出去就行了。抽象地来说，当我们选择相互正交的特征来描述一个事物时，是最简洁的。
\;\;\,\quad 基于这个认识，我们可以设想，可不可以使用一组特定的相互正交的信号和一个特定的关系去描述所有信号呢？把原本复杂的信号分解开，然后用几个系数去简洁地表示它。这就用到了正交函数集——一个函数集合内的所有函数之间两两正交。这样的函数集有很多，比如 { 1 , x , x 2 , x 3 , . . . , x n } \{1,x,x^2,x^3,...,x^n\} {1,x,x2,x3,...,xn}，或者是 { 1 , cos ( x ) , sin ( x ) , cos ( 2 x ) , sin ( 2 x ) , . . . } \{1,\cos(x),\sin(x),\cos(2x),\sin(2x),...\} {1,cos(x),sin(x),cos(2x),sin(2x),...}3。我们可以把一个信号表示为函数集内各个函数的加权和，即
f ( x ) = ∑ i = 1 n c i g i ( x ) , ⟨ g i , g j ⟩ = 0 ( i ≠ j ) , ∀ i f(x)=\sum_{i=1}^{n}{c_ig_i(x)}, \langle{g_i,g_j}\rangle=0(i \neq j) ,\forall i f(x)=i=1∑ncigi(x),⟨gi,gj⟩=0(i̸=j),∀i
\;\;\,\quad 正交的意义。除了用于简洁地分解信号外，正交还有很多用途。回到正交本身，它意味着不相关，也就是互相正交的东西之间是不会相互影响的，无论是物理上还是数学上。这就给我们如何充分地利用资源带来了一个思路。比如“你走你的阳关道，我走我的独木桥”，如果能找到足够多的阳关道和独木桥，就能让成千上万的人同时在路上走。只要能找到足够多的正交空间，就有可能让足够多的信息在同一环境下传输。这并不抽象，比如从时间轴上看，0-1s和1-2s是互不影响（正交）的，那就可以在其他条件（比如频率）都一样的情况下，把0-1s的时间资源分配给用户1，1-2s给用户2，这就是一种简单的正交多址技术。4
\;\;\,\quad 除了使信号在不同正交空间传输，也可以尝试将信息放入不同正交空间，去构成一个在多维度都有信息的信号。信号本身就是包含多维信息的，只不过为了方便，一般就只利用一下时域或者频域，而在保密通信用的变换域通信技术中，我们在每个域中都放入不同信息（有真有假）来欺骗敌人。这就是正交空间的另外一种用途。当然，还能有更多的方式，只有想不到，没有做不到。
\;\;\,\quad 需要注意的是，物理上的正交和数学上的正交可能有所差别。在物理上正交的事物可能可以在数学上用一些工具综合起来进行分析。比如，为什么傅里叶变换可以实现时间信号和频率信号的转换，但又说时域和频域是正交的？这个正交指的是物理上的不相关。比如，在某一个时间点，我们无法通过当前的时刻值算出有什么频率；同样的，就算获得某个频率的强度值，也无法推算出它是什么时刻出现的，这就是时域和频域物理上的不相关。至于傅里叶变换中有时域信号到频谱的转换（看似相关），则是因为它是对一段时间内的信号进行分析的，这段信号内既包含了时域信息也包括了频域信息，FT只是起一个筛子的作用，把频域信息提取出来而已，并不是时域和频域有相关性。
\;\;\,\quad 相关和正交，简单又不简单。
相关和相干是不一样的！可能会先学到“相干”这个东西，在此先做说明以免混淆。相干解调是指利用乘法器，输入一路与载频相干（同频同相）的参考信号与载频相乘。暂时不懂没关系，只要知道是完全不同的两个东西就行。 ↩︎
严格地说，这是实函数能量信号， f 1 f_1 f1对 f 2 f_2 f2的相关函数 R 12 ( τ ) R_{12}(\tau) R12(τ)； R 21 ( τ ) = ∫ − ∞ + ∞ f 2 ( t ) ⋅ f 1 ( t − τ ) d t R_{21}(\tau)=\int_{-\infty}^{+\infty}{f_2 (t)·f_1 (t-\tau)}dt R21(τ)=∫−∞+∞f2(t)⋅f1(t−τ)dt。如果是复能量信号，要对 f 2 f_2 f2求共轭， R 12 ( τ ) = ∫ − ∞ + ∞ f 1 ( t ) ⋅ f 2 ∗ ( t − τ ) d t R_{12}(\tau)=\int_{-\infty}^{+\infty}{f_1 (t)·f_2^* (t-\tau)}dt R12(τ)=∫−∞+∞f1(t)⋅f2∗(t−τ)dt。还有对于功率信号的，详细看信号与系统课本中的说明。 ↩︎
这就是傅里叶变换中要用到的三角函数集。 ↩︎
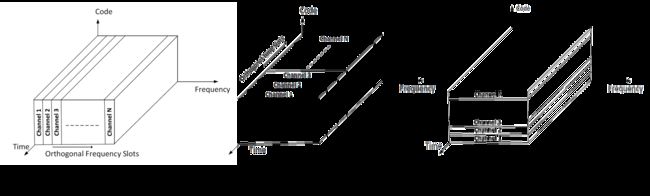
正交多址（Orthogonal Multiple Access），简单地说就是切蛋糕，有TDMA（时分多址）、FDMA（频分多址）、CDMA（码分多址）、SDMA（空分多址）等。对应的还有非正交多址技术（NOMA: non-orthogonal Multiple Access）。
↩︎