科学计算与Matlab笔记：第2章：Matlab矩阵处理

1. 特殊矩阵

通用的特殊矩阵

>zeros函数：产生全0的矩阵，即零矩阵

>ones函数：产生全1的矩阵，即1矩阵

>eye函数：产生对角线为1的矩阵。当矩阵为方阵时则得到一个单位阵

>rand函数：产生0~1区间均匀分布的随机矩阵

>randn函数：产生均值为0，方差为1的标准正态分布随机矩阵。

 

zeros函数的调用格式：

>zeros(m): 产生mxm的零矩阵

>zeros(m,n):产生mxn零矩阵

>zeros(size(A)):产生与矩阵A同样大小的零矩阵

>> A=zeros(2,3)

A =

     0     0     0
     0     0     0

>> zeros(size(A))

ans =

     0     0     0
     0     0     0

>> zeros(size(reshape(A,3,2)))

ans =

     0     0
     0     0
     0     0
 

例1 首先产生5阶两位随机矩阵A，在产生均值为0.6，方差为0.1的5阶正态分布随机矩阵B，最后验证（A+B）I=IA+BI(I为单位矩阵)

>rand函数：产生0~1开区间均匀分布的随机数x

>fix(a+(b-a+1)*x):产生a~b区间上均匀分布的随机整数

>randn函数：产生均值为0，方差为1的标准正态分布随机数x

>u+cx：得到均值为u，方差为c^2的随机数

>> A=fix(10+(99-10+1)*rand(5));
>> B=0.6+sqrt(0.1)*rand(5);
>> C=eye(5);
>> (A+B)*C==C*A+B*C

ans =

     1     1     1     1     1
     1     1     1     1     1
     1     1     1     1     1
     1     1     1     1     1
     1     1     1     1     1

 

用于专门学科的特殊矩阵

（1）魔方矩阵

>> M=magic(3)

M =

     8     1     6
     3     5     7

     4     9     2

>n阶魔方阵有1，2，3，……，n^2个整数组成，且每行每列以及主、副对角线上各n个元素之和都相等。

>n阶魔方方阵每行每列元素的的和为（1+2+3+...+n^2）/n = (n+n^3)/2

>MATLAB函数magic(n)产生一个特定的魔方阵

例2 产生8阶魔方矩阵，求其每行每列元素的和。

>> M=magic(8);
>> sum(M(1,:))

ans =

   260

>> sum(M(:,1))

ans =

   260

>> trace(M)

ans =

   260

 

（2）范德蒙行列式

在MATLAB中，函数vander(V)生成以向量V为基础的范德蒙矩阵

>> A=vander(1:5)

A =

     1     1     1     1     1
    16     8     4     2     1
    81    27     9     3     1
   256    64    16     4     1
   625   125    25     5     1

范德蒙矩阵常用在各种通信系统的纠错编码中，如Reed-Solomon编码以范德蒙矩阵为基础

（3）希尔伯特矩阵

希尔伯特矩阵是著名的病态矩阵：矩阵中任何一个元素微小的变动，都会引起矩阵值以及逆矩阵的值的较大的扰动，病态程度与矩阵的阶数有关，阶数越高，病态程度越严重。

在MATLAB中，生成n阶希尔伯特的函数为：hilb(n):

>> format rat   //以有理数格式显示
>> H=hilb(4)

H =

       1              1/2            1/3            1/4     
       1/2            1/3            1/4            1/5     
       1/3            1/4            1/5            1/6     
       1/4            1/5            1/6            1/7

（4）伴随矩阵（特征值为多项式方程的根）

（4）伴随矩阵

MATLAB生成伴随矩阵的函数是compan（p），其中p是一个多项式的系数向量，高次幂系数排在前，低次幂系数排在后。

例如， 生成多项式(x^3 - 2x^2 - 5x + 6)的伴随矩阵

>>    p=[1,-2,-6,6];
>> A=compan(p)

A =

       2              6             -6       
       1              0              0       
       0              1              0 

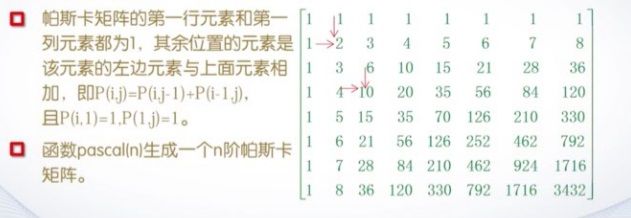
（5）帕斯卡矩阵

例3 生成5阶帕斯卡矩阵，验证他的逆矩阵的所有元素也为矩阵

>> format rat
>> P=pascal(5)

P =

       1              1              1              1              1       
       1              2              3              4              5       
       1              3              6             10             15       
       1              4             10             20             35       
       1              5             15             35             70       

>> inv(P)

ans =

       5            -10             10             -5              1       
     -10             30            -35             19             -4       
      10            -35             46            -27              6       
      -5             19            -27             17             -4       
       1             -4              6             -4              1
 

2. 矩阵变换

>对角矩阵：只有对角线上有非零元素的矩阵

>数量矩阵：对角线上的元素相等的对角矩阵

>单位矩阵：对角线上的元素都为1的对角矩阵

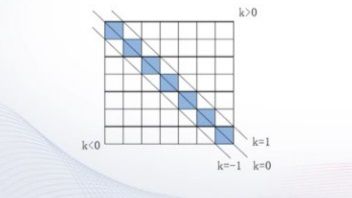
（1）提取矩阵的对角线元素

>diag(A):提取矩阵A的主对角线元素，生成一个列向量

>diag(A,k):提取矩阵A的第k条对角线元素，生成一个列向量

主对角线：k=0，向上，向下分别为k=1，2，…… /k=-1，-2，……对角线

（2）构造对角阵

>diag(V):以向量V为主对角元素，产生对角矩阵

>diag(V,k)：以向量V为第k条对角元素，产生对角矩阵

例1 先建立5x5矩阵A，然后将A的第1行元素乘以1，第2行元素乘以2，……，第5行元素乘以5

>> A=[7,0,1,0,5;3,5,7,4,1;4,0,3,0,2;1,1,9,2,3;1,8,5,2,9]

A =

       7              0              1              0              5       
       3              5              7              4              1       
       4              0              3              0              2       
       1              1              9              2              3       
       1              8              5              2              9       

>> D=diag(1:5)

D =

       1              0              0              0              0       
       0              2              0              0              0       
       0              0              3              0              0       
       0              0              0              4              0       
       0              0              0              0              5       

>> D*A

ans =

       7              0              1              0              5       
       6             10             14              8              2       
      12              0              9              0              6       
       4              4             36              8             12       
       5             40             25             10             45 

要将A的各列元素分别乘以对角阵的对角线元素，如何实现？

>> A*D

ans =

       7              0              3              0             25       
       3             10             21             16              5       
       4              0              9              0             10       
       1              2             27              8             15       
       1             16             15              8             45       
 

三角阵

>上三角阵：矩阵的对角线以下的元素全为0的矩阵

>下三角阵：矩阵的对角线以上的元素全为0的矩阵

（1）上三角阵

>triu（A）：提取矩阵A的主对角线及以上的元素

>triu（A，k）：提取矩阵A的第k条对角线及以上的元素

>> triu(ones(4),-1)

ans =

       1              1              1              1       
       1              1              1              1       
       0              1              1              1       

       0              0              1              1

 

（2）下三角阵

在MATLAB中，提取矩阵A的下三角矩阵的函数是tril，其用法与triu函数完全相同。

>tril（A）：提取矩阵A的主对角线及以下的元素

>tril（A，k）：提取矩阵A的第k条对角线及以下的元素

>>  tril(ones(4),-1)

ans =

       0              0              0              0       
       1              0              0              0       
       1              1              0              0       
       1              1              1              0       
 

矩阵的转转置

>转置运算符是小数点后面接单引号（.'）

>共扼转置，其运算符是单引号（‘），它在转置的基础上还要提取每个数的复共轭

>> A=[1,3;3+4i,1-2i]

A =

       1        +    0i             3        +    0i      
       3        +    4i             1        -    2i      

>> A.'

ans =

       1        +    0i             3        +    4i      
       3        +    0i             1        -    2i      

>> A'

ans =

       1        +    0i             3        -    4i      
       3        +    0i             1        +    2i      
 

矩阵的旋转

rot90（A，k）：将矩阵A逆时针方向旋转90°的k倍，当k为1时可以省略

>> A=[1,3,2;-3,2,1;4,1,2]

A =

       1              3              2       
      -3              2              1       
       4              1              2       

>> rot90(A)

ans =

       2              1              2       
       3              2              1       
       1             -3              4       

>> rot90(A,2)

ans =

       2              1              4       
       1              2             -3       
       2              3              1 
 

>fliplr(A):对矩阵A实施左右翻转

>flipud(A):对矩阵A实施上下翻转

A =

       1              3              2       
      -3              2              1       
       4              1              2       

>> flipud(A)

ans =

       4              1              2       
      -3              2              1       
       1              3              2       

>> fliplr(A)

ans =

       2              3              1       
       1              2             -3       
       2              1              4       
 

例2 验证魔方方阵的主对角线，副对角线元素之和相等

>> A=magic(5)

A =

      17             24              1              8             15       
      23              5              7             14             16       
       4              6             13             20             22       
      10             12             19             21              3       
      11             18             25              2              9      
>> D1=diag(A);
>> sum(D1)

ans =

      65       
 

>> B=flipud(A)

B =

      11             18             25              2              9       
      10             12             19             21              3       
       4              6             13             20             22       
      23              5              7             14             16       
      17             24              1              8             15 
>> D2=diag(B);
>> sum(D2)>

ans =

      65       

矩阵的求逆

>对于一个方阵A，如果存在一个与其相同阶的方阵B，使得AB=BA=I（I为单位矩阵），则称B为A的逆矩阵，当然A也是B的逆矩阵

>inv（A）：求方阵A的逆矩阵

 

3. 矩阵求值

方阵的行列式

>把一个方阵看作一个行列式，并对其按行列式的规则求值，这个值就称为方阵所对应的行列式的值

>det(A):求方阵A所对应的行列式的值

矩阵的秩

>矩阵线性无关的行数和列数成为矩阵的秩

>rank(A): 求矩阵A的秩

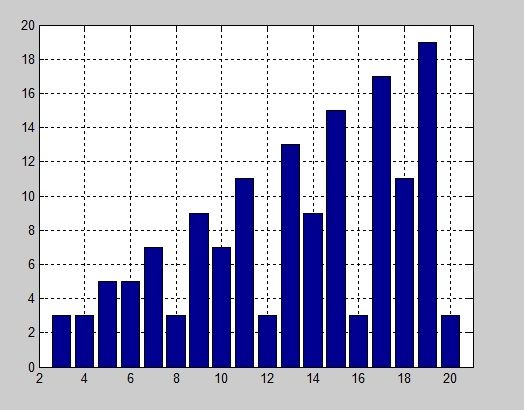
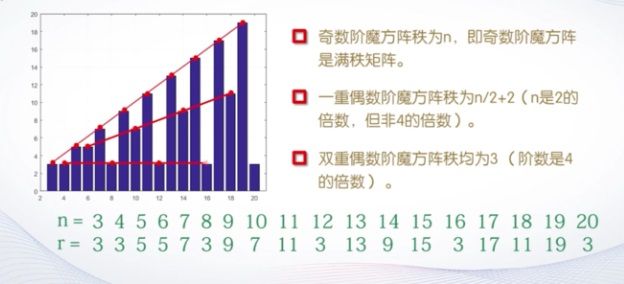
例2 求3~20阶魔方阵的秩

>> for n=3:20
r(n)=rank(magic(n));
end
>> bar(r)
>> grid on
>> axis([2,21,0,20])

矩阵的迹

>矩阵的迹等于矩阵的对角线元素之和，也等于矩阵的特征值之和

>trace(A):求矩阵A的迹

>> A=[1,3,2;-3,2,1;4,1,2]

A =

       1              3              2       
      -3              2              1       
       4              1              2       

>> b=trace(A)

b =

       5       

>> t=sum(diag(A))

t =

       5   

向量和矩阵的范数

矩阵或向量的范数用于定义矩阵或向量在某种意义下的长度

矩阵的条件数

>矩阵A的条件数等于A的范数与A的逆矩阵的范数的乘积

>条件数越接近于1，矩阵的性能越好，反之，矩阵的性能越差

在MATLAB中，计算矩阵A的3种条件数的函数是：

>cond(A,1):计算A的1-范数下的条件数

>cond(A,2)或cond(A):计算A的2-范数下的条件数

>cond(A,inf):计算A的正无穷-范数下的条件数

例3 求2~10阶希尔伯特矩阵的条件数

>> for n=2:10
c(n)=cond(hilb(n));
end
>> format long
>> c'

ans =

   1.0e+13 *

                   0
   0.000000000001928
   0.000000000052406
   0.000000001551374
   0.000000047660725
   0.000001495105864
   0.000047536735692
   0.001525757525282
   0.049315438266897
   1.602457362635516

>> c

c =

   1.0e+13 *

  Columns 1 through 5

                   0   0.000000000001928   0.000000000052406   0.000000001551374   0.000000047660725

  Columns 6 through 10

   0.000001495105864   0.000047536735692   0.001525757525282   0.049315438266897   1.602457362635516
 

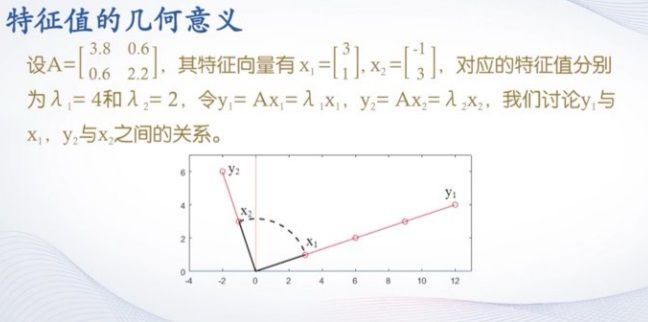
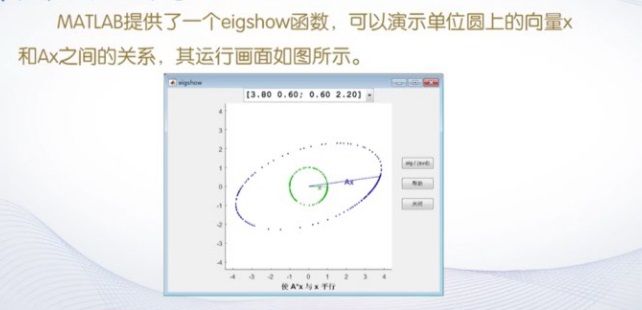
4. 矩阵的特征值与特征向量

矩阵特征值的数学定义

设A是n阶方阵，如果存在常数λ和n维非零列向量x，是的等式Ax=λx成立，则称λ为A的特征值，x是对应特征值λ的特征向量

函数调用格式有两种：

>E=eig(A):求矩阵A的全部特征值，构成向量E

>[X,D]=eig(A):求矩阵A的全部特征值，构成对角阵D，并产生矩阵X，X各列是相应的特征向量

>> A=[1,1,0;1,0,5;1,10,2]

A =

     1     1     0
     1     0     5
     1    10     2

>> [X,D]=eig(A)

X =

   0.072196186226992   0.975064063761619   0.088619224195266
   0.523368974057523  -0.075013465822403  -0.635606218080313
   0.849042182514069  -0.208861321230112   0.766910274178584


D =

   8.249260679947781                   0                   0
                   0   0.923068166892527                   0
                   0                   0  -6.172328846840313

>> A*X(:,1)

ans =

   0.595565160284515
   4.317407098797336

   7.003970291830358

>> D(1)*X(:,1)

ans =

   0.595565160284514
   4.317407098797333

   7.003970291830355

 

 

>> R=[-1,2,0;2,-4,1;1,1,-6];
>> S=[1,2;2,3];
>> A=[R,zeros(3,2);zeros(2,3),S];
>> [X1,D1]=eig(R)

X1 =

   0.855336847706575   0.451748808798346   0.189889692402449
   0.470284611344323  -0.839453879712591  -0.511105640718618
   0.217327543786097  -0.302059923830942   0.838279743728139


D1 =

   0.099647729675864                   0                   0
                   0  -4.716463058067783                   0
                   0                   0  -6.383184671608076

>> [X2,D2]=eig(S)

X2 =

  -0.850650808352040   0.525731112119133
   0.525731112119133   0.850650808352040


D2 =

  -0.236067977499790                   0
                   0   4.236067977499790

>> [X3,D3]=eig(A)

X3 =

   0.855336847706575   0.451748808798346   0.189889692402449                   0                   0
   0.470284611344323  -0.839453879712591  -0.511105640718618                   0                   0
   0.217327543786097  -0.302059923830942   0.838279743728139                   0                   0
                   0                   0                   0  -0.850650808352040  -0.525731112119133
                   0                   0                   0   0.525731112119133  -0.850650808352040


D3 =

   0.099647729675864                   0                   0                   0                   0
                   0  -4.716463058067783                   0                   0                   0
                   0                   0  -6.383184671608076                   0                   0
                   0                   0                   0  -0.236067977499790                   0
                   0                   0                   0                   0   4.236067977499790

>>

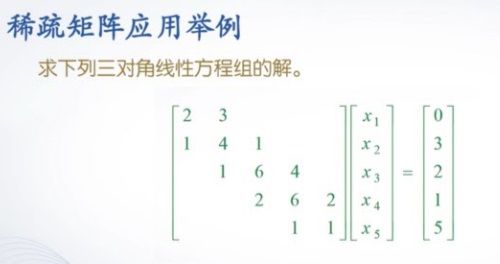
5. 稀疏矩阵

矩阵的存储方式：完全存储方式+稀疏存储方式

稀疏存储方式只存储矩阵的非零元素的值及其位置，即行号和列号

注意：采用稀疏存储方式时，矩阵元素的存储顺序并没有改变，也是按列的顺序进行存储

>> A=sparse(eye(5))

A =

   (1,1)        1
   (2,2)        1
   (3,3)        1
   (4,4)        1
   (5,5)        1

>> B=full(A)

B =

     1     0     0     0     0
     0     1     0     0     0
     0     0     1     0     0
     0     0     0     1     0
     0     0     0     0     1

>> whos
  Name      Size            Bytes  Class     Attributes

  A         5x5               128  double    sparse    
  B         5x5               200  double 

>> A=sparse([1,2,2],[2,1,4],[2,5,-7])

A =

   (2,1)        5
   (1,2)        2
   (2,4)       -7

>> B=full(A)

B =

     0     2     0     0
     5     0     0    -7

>> A=[2,2,1;2,1,-1;2,4,3]

A =

     2     2     1
     2     1    -1
     2     4     3

>> B=spconvert(A)   //最后一列从小到大按行排列？

B =

   (2,1)       -1
   (2,2)        1

   (2,4)        3

>> A=[11,0,0,12,0,0;0,21,0,0,22,0;0,0,31,0,0,32;41,0,0,42,0,0;0,51,0,0,52,0]

A =

    11     0     0    12     0     0
     0    21     0     0    22     0
     0     0    31     0     0    32
    41     0     0    42     0     0
     0    51     0     0    52     0

>> [B,d]=spdiags(A)

B =

     0    11    12
     0    21    22
     0    31    32
    41    42     0
    51    52     0


d =

    -3
     0
     3

>> A=spdiags(B,d,5,6)

A =

   (1,1)       11
   (4,1)       41
   (2,2)       21
   (5,2)       51
   (3,3)       31
   (1,4)       12
   (4,4)       42
   (2,5)       22
   (5,5)       52

   (3,6)       32

>> kf1=[1;1;2;1;0];
>> k0=[2;4;6;6;1];
>> k1=[0;3;1;4;2];
>> B=[kf1,k0,k1];
>> d=[-1;0;1];
>> A=spdiags(B,d,5,5);
>> f=[0;3;2;1;5];
>> x=A\f

x =

  -0.166666666666667
   0.111111111111111
   2.722222222222222
  -3.611111111111111

   8.611111111111111

注意：当参与运算的数据对象不全是稀疏存储矩阵时，所得结果是完全存储形式。